Kezdőlap


Cím:	Megmaradási tételek a klasszikus mechanikában
Szerző(k):	Bodó Zalánné
Füzet:	1970/szeptember, 33 - 40. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bevezetés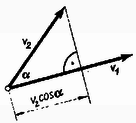
Azok számára, akik csak a vektorok összeadását, kivonását és skalárral való szorzatát ismerik, röviden ismertetjük a vektoralgebrában definiálható szorzásokat és azoknak (egyik) szokásos jelölését. Így a következő mechanikai törvények felírása, igazolása stb. az ismertetett matematikai jelölésekkel a koordinátás írásmódnál sokkal rövidebben és egyszerűbben történhet.
Vektorok skaláris szorzatán értjük a két vektor abszolút értékének és a két vektor által bezárt szög cosinusának szorzatát. Két vektor skaláris szorzata tehát skaláris mennyiség. A skaláris szorzatot a vektorok jelei közé tett ponttal jelölhetjük.

1. ábra

Tehát (1. ábra):

\begin{matrix} v_{1} \cdot v_{2} = v_{1} v_{2} cos α . \end{matrix}

(1)

A skaláris szorzat koordinátákkal kifejezve:

\begin{matrix} v_{1} \cdot v_{2} = \sqrt[]{v_{1 x}^{2} + v_{1 y}^{2} + v_{1 z}^{2}} \cdot \sqrt[]{v_{2 x}^{2} + v_{2 y}^{2} + v_{2 z}^{2}} cos α . \end{matrix}

(2)

Az előbbi definícióból az is megállapítható, hogy mivel

v_{2} cos α

v_{2}

vektor hosszának a

v_{1}

vektor irányába eső előjeles vetülete, a skaláris szorzat egy vektor abszolút értékének és egy másik vektor összetevő abszolút értékének előjeles szorzatát jelenti. Így pl., ha az egyik vektor a testre ható erő

(F)

, a másik a test elmozdulása

(s)

, skaláris szorzatuk definíció szerint éppen az erő által végzett munka:

\begin{matrix} W = F \cdot s . \end{matrix}

(3)

A skaláris szorzás eredménye nyilván pozitív

(α < π / 2)

, negatív

(α > π / 2)

vagy nulla lehet. Nulla pl. akkor, ha a skaláris szorzat két tényező vektoru egymásra merőleges

(α = π / 2)

. A skaláris szorzat tehát abban különbözik a ,,közönséges'' szorzattól, hogy értéke akkor is nulla lehet, ha egyik tényezője sem nulla (nulla hosszúságú vektor).
Belátható, hogy a skaláris szorzatra érvényesek az alábbi műveleti szabályok: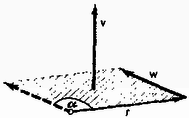

\begin{matrix} v_{1} \cdot v_{2} = v_{2} \cdot v_{1}, \\ (λ v_{1}) \cdot v_{2} = λ (v_{1} \cdot v_{2}) (λ szám), & (4) \\ v_{1} \cdot (v_{2} + v_{3}) = v_{1} \cdot v_{2} + v_{1} \cdot v_{3} . \end{matrix}

2. ábra

Két vektornak vektoriális szorzatán azt a vektort értjük, melynek nagyságát a két vektor által kifeszített paralelogramma területe (1. 2. ábra:

v = r w sin α

) adja meg, iránya pedig merőleges e paralelogramma síkjára úgy, hogy

r

w

és

v

(ebben a sorrendben) jobbsodrású rendszert alkot. (

r

jobb kezünk hüvelykujja,

w

mutatóujja,

v

középső ujja felé mutat. L. a 3. ábrát.)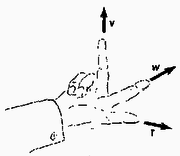

3. ábra

A fizikában a vektoriális szorzás többek között a különböző vektorok nyomatékának definíciójánál kap szerepet. Valamely

w

vektornak nyomatékán az

r

(a koordináta‐rendszer

O

kezdőpontjából a vizsgált helyre mutató) helyzetvektornak és a w vektornak vektoriális szorzatát értjük. A vektoriális szorzást a

\times

jellel jelölhetjük:

\begin{matrix} v = r \times w . \end{matrix}

(5)

Így pl. a Kepler‐törvényekben szereplő területsebesség nem más, mint a sebességnyomaték fele.
Az erő

(F)

nyomatékát az erő

O

pontra vonatkozó forgatónyomatékának

(M)

hívják. Az

M

vektorból az

O

ponton keresztülmenő valamilyen tengelyre vonatkozó forgatónyomatékot úgy kapjuk meg, hogy a fenti forgatónyomaték vektornak meghatározzuk a tengely irányú összetevőjét (vetületét).
Az (5)-tel definiált

v

vektor iránya és nagysága természetesen általában függ a koordináta‐rendszerünk kezdőpontjának megválasztásától, az

O

pont helyzetétől, mert az

r

vektor kezdőpontja ebből indul ki. A

v

vektor azonban nem változik, ha az

r

vektor végpontját

w

irányába eltoljuk (4. ábra).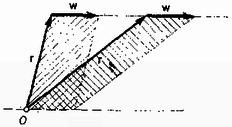

4. ábra

A paralelogramma területe, alap szorozva a magassággal, az eltolás után változatlan marad. Az

r

vektor tehát a

w

vektor ,,támadásvonalának'' tetszőleges pontjába mutathat. Az is könnyen belátható, hogyha

w

irányát megfordítjuk,

v

iránya is ellenkezőre változik. A vektoriális szorzat

0

(nulla hosszúságú vektor) lehet akkor is, ha a tényezők egyike sem

0

. Ti. akkor, ha

α = 0

vagy

π

, vagyis amikor a tényezők párhuzamosak. A vektoriális szorzás a skaláris szorzással ellentétben azonban nem kommutatív, hanem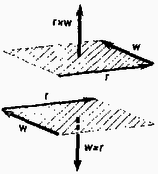

\begin{matrix} r \times w = - w \times r, \end{matrix}

a tényezők sorrendjének felcserélésével a

v

szorzatvektor értelme éppen ellentétesre változik (5. ábra).

5. ábra

Továbbá többek között igazak az alábbi műveleti szabályok:

\begin{matrix} λ (v_{1} \times v_{2}) = λ v_{1} \times v_{2}, \\ v_{1} \times (v_{2} + v_{3}) = (v_{1} \times v_{2}) + (v_{1} \times v_{3}) . & (7) \end{matrix}

A klasszikus mechanika mozgástörvénye szerint valamely tömegpont (pontszerűnek tekinthető test) impulzusának időegységre eső megváltozását (pontosabban az idő szerinti differenciálhányadosát) minden időpontban a ható erők vektori összege határozza meg. Az impulzus pedig a tömeg és az elmozdulás idő szerinti differenciálhányadosának (sebességnek) a szorzata. Ezért ha térben és időben ismerjük a testre ható erőket, a test mozgásának meghatározása, a mozgásegyenletek megoldása már ,,csak'' matematikai probléma. Bonyolultabb erők esetén ez azonban igen nehéz számítási feladat lehet, sokszor olyan hosszadalmas is, hogy ésszerű idő alatt csak a modern számítógépek segítségével oldható meg. (L. pl. az űrhajózás pályaszámítását.) Éppen ezért nagyon lényeges, hogy sokszor a mozgásra igen értékes információkat nyerhetünk a mozgásegyenletek megoldása nélkül is, akkor, ha a fellépő erők speciális feltételeket teljesítenek. Legtöbb esetben ez az információ a mozgások folyamán bizonyos mennyiségek állandó voltában, azaz megmaradási elvek, tételek alakjában jelentkezik. A következőkben a klasszikus mechanika három ilyen megmaradási tételével fogunk foglalkozni.

A mechanikai energia megmaradási tétele

Az olyan erőt (pontosabban erőteret), amelynél az erő

(F)

által végzett munka nem függ attól, hogy milyen pályán kerül valamely tömegpont a tér egyik (pl.

A

) pontjából a tér másik (pl.

B

) pontjába (6. ábra), hanem ez a munka csak a kezdő és végpont helyzetétől függ, konzervatív erőnek (erőtérnek) nevezzük. Ilyen erő pl. a tömegvonzás, az elektrosztatikus vonzás vagy taszítás, az ideális rugóerő stb. Nem konzervatív erő pl. a súrlódás, ennél ugyanis a súrlódó erő munkája a megtett úttal arányos, tehát a különböző hosszúságú, de azonos végpontú pályákra különböző. A konzervatív erők előbbi tulajdonsága lehetővé teszi azt, hogy az

F

erő hatása alatt levő testekhez egyértelműen potenciális (helyzeti) energiát rendeljünk. Kiválaszthatunk a térben egy tetszőleges pontot (pl. a 6. ábrán

A

-t), ahol a test potenciális energiáját önkényesen

0

-nak vesszük fel.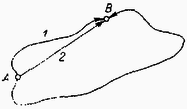

6. ábra

Látni fogjuk, hogy az energiamegmaradási tételben tulajdonképpen csak a potenciális energia‐különbség kap szerepet, ezért a helyzeti energiának nulla szintjét tetszőlegesen vehetjük fel. A tér valamelyik másik (pl.

B

) pontjában a testnek az

F

erőtől származó potenciális energiáját azzal a munkával definiálhatjuk, amelyet az erő akkor végez, amikor a test a

B

pontból valamilyen (az előzőek szerint tetszőleges) pályán

A

-ba kerül. Több konzervatív erő esetén mindegyik erőhöz rendelhetünk egy - egy potenciális energiát, és azok összege adja meg a test teljes potenciális energiáját. A konzervatív erő és a hozzá rendelhető potenciális energia előbbi definíciójának birtokában igazolhatjuk a mechanikai energia megmaradási tételét:
Ha a tömegpontra ható összes erők konzervatívak, akkor a tömegpontnak a kinetikus (mozgási) energiájából és potenciális (helyzeti) energiájából összetevődő teljes mechanikai energiája a mozgás folyamán állandó marad:

\begin{matrix} E_{kin} + E_{pot} = E_{mech} = állandó . \end{matrix}

(8)

Vizsgáljuk meg ugyanis az energiákat, amikor a test mozgása folyamán a 7. ábrán látható módon az

l

pályáján a

B

pontból a közeli

C

pontba mozdul el (elmozdulása legyen a kis

Δ r

vektor).

7. ábra

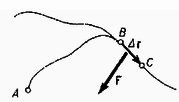Kössük össze az

A

és

B

pontot valamilyen tetszőleges görbével és számítsuk ki a test

C

pontbeli potenciális energiáját az

A - B - C

úton végzett munka segítségével, miközben hat rá az

F

konzervatív erő. Az

F

erő munkája az

A - B

úton definíció szerint a

B

pontbeli potenciális energia

(- 1)

-szerese, a

B - C

úton

F \cdot Δ r

, a kettő összege definíció szerint a

C

pontbeli potenciális energia

(- 1)

-szerese kell, hogy legyen. Tehát

\begin{matrix} - E_{pot C} = - E_{pot B} + F \cdot Δ r . \end{matrix}

(9)

Legyen a test sebessége a

B

pontban

v

, a

C

pontban

v + Δ v

. Ha a

C

pontot eléggé közel választjuk

B

-hez, mivel az

F

erő véges,

Δ v

tetszőlegesen kicsivé tehető, olyan kicsivé, hogy

| Δ v |

-hez képest

| Δ v |^{2}

már elhanyagolható nagyságú lehet. Így a kinetikus energiák:

\begin{matrix} E_{kin B} = \frac{m}{2} v^{2} = \frac{m}{2} v \cdot v, & (10) \\ E_{kin C} = \frac{m}{2} (v + Δ v) \cdot (v + Δ v) = \\ = \frac{m}{2} v^{2} + m v \cdot Δ v + \frac{m}{2} (Δ v \cdot Δ v) \approx & (11) \\ \approx E_{kin B} + m \frac{Δ r}{Δ t} \cdot Δ v = E_{kin B} + m \frac{Δ v}{Δ t} \cdot Δ r = E_{kin B} + F \cdot Δ r . \end{matrix}

(11)-ből

F \cdot Δ r

-t kifejezve, (9)-be helyettesítve és rendezve:

\begin{matrix} E_{pot C} - E_{pot B} = E_{kin B} - E_{kin C} . \end{matrix}

(12)

Amekkora a potenciális energia növekedése, ugyanakkora a kinetikus energia csökkenése. (12)-t átrendezve:

\begin{matrix} E_{pot C} - E_{kin C} = E_{pot B} - E_{kin B} . \end{matrix}

(13)

Tehát a test mozgása folyamán (az egymás utáni közeli pontokban és így belátható, hogy az egész pályáján is) a mechanikai energia állandó, megmarad (mintegy konzerválódik, ezért nevezzük az ilyen erőket konzervatív erőknek).
A mechanikai energia megmaradási tételét pl. a 8. ábrán vázolt kísérlettel, ill. feladattal demonstrálhatjuk.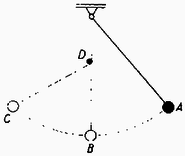

8. ábra

Kérdés, milyen magasra emelkedik az

A

pontból elengedett, fonalingán levő test, ha a fonalat a

D

-nél elhelyezett szöggel megakasztjuk. Mivel a

C

pontban ugyanúgy, mint az

A

pontban a mozgási energia

0

, ha az erők konzervatívok (amikor a súrlódási, közegellenállást és a többi nem konzervatív erőt elhanyagolhatjuk), előre megmondhatjuk, hogy ugyanolyan magasra emelkedik, mint az

A

pontban volt, mert a potenciális energiáknak meg kell egyezniük. A mozgásegyenletek bonyolult megoldása nélkül is kísérletünk, ill. feladatunk eredményét előre meg tudjuk mondani. E feladatban kényszererő is szerepelt. A mechanikai energia megmaradási tételének alkalmazásakor tudnunk kell azt is, hogy az olyan erő, amely a mozgó testet valamely pályára kényszeríti, mindig merőleges e pályára, és így munkája mindig nulla. Ezért az energia‐tétel alkalmazásakor az ilyen kényszererők egyszerűen figyelmen kívül hagyhatók.
Végül megjegyezzük, hogy az energia fogalma az ismertetett meggondolások szerint eredetileg a mechanikában alakult ki. A mechanikai energia megmaradási tétele azonban nem általános jellegű, csak konzervatív erőkre érvényes. Ennek ellenére az energia megmaradásának elve a mechanikai, sőt a klasszikus fizika területén túlmenő (pl. kémia) általános tapasztalati törvénynek bizonyult. Ha a mechanikai energiákon kívül a természetben előforduló egyéb energiákat is figyelembe vesszük, akkor már általánosan érvényes, hogy energia nem vész el. A nem konzervatív erő ellenében végzett munka során eltűnő mechanikai energia más energiafajtává alakul át. Pl. A súrlódási erő ellenében végzett munka eredményeképpen általában a testek felmelegednek, és a fejlődő hő azoknak ún. belső (hőtani) energiáját növeli meg. Ezt hívják a hőtan I. főtételének.

Az impulzus megmaradási tétele
Egyetlen tömegpont impulzusán

(I)

, a tömegének

(m)

és a sebesség vektorának

(v)

szorzatát értjük. Az impulzust szokás még mozgásmennyiségnek vagy lendületnek is nevezni. A tömegpontokból álló rendszer impulzusán az egyes tömegpontok impulzusainak vektori összegét értjük:

\begin{matrix} I = \sum m_{i} v_{i} . \end{matrix}

(14)

A tömegpontokból álló olyan rendszert, amelynek tagjai csak egymásra fejtenek ki erőhatást, vagyis a rendszeren kívül levő testek nem fejtenek ki erőket, zárt rendszernek, az egymás között kifejtett erőket pedig belső erőknek nevezzük.
Az impulzus megmaradási tétele a következő: belső erők a rendszer impulzusát nem változtatják meg, vagyis zárt rendszernek az impulzusa megmarad. Ez a tétel a newtoni mozgástörvényekből egyszerűen következik. Vizsgáljuk meg ugyanis pl. a kezdeti helyzetükkel a 9. ábrán felrajzolt három tömegpontból álló zárt rendszer impulzusának megváltozását

Δ t

idő ala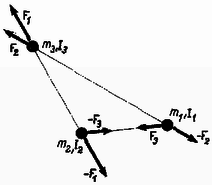tt.

9. ábra

Az egyszerűség kedvéért csak kevés számú tömegpontot választottunk és feltételeztük, hogy két test közötti erőhatás a két testet összekötő egyenes mentén hat (centrális erők). Könnyen belátható, hogy a következő meggondolásaink általánosságban tetszőleges számú tömegpontból álló zárt rendszerre is érvényesek. Általában bármely két pontszerű test között lehet erőhatás, összesen tehát az ábrán látható hat (belső) erő léphet fel. Az ábrán már tekintetbe vettük azt is, hogy ezek az erők a hatás - ellenhatás newtoni törvénye szerint párosával egyenlő nagyságúak, de ellentétes irányúak. Mindegyik tömegpont impulzusának egységnyi idő alatt bekövetkező megváltozása az illető tömegpontra ható erők vektori összegével egyenlő. Ezért

\begin{matrix} Δ I_{1} = (- F_{2} + F_{3}) Δ t, \\ Δ I_{2} = (- F_{1} - F_{3}) Δ t, & (15) \\ Δ I_{3} = (F_{1} + F_{2}) Δ t . \end{matrix}

Ezeket az egyenleteket összeadva:

\begin{matrix} Δ I_{1} + Δ I_{2} + Δ I_{3} = Δ I = 0. \end{matrix}

(16)

Tehát minden időpontban a rendszer impulzusának megváltozása nulla (nulla hosszúságú vektor), vagyis a tömegpontok a belső erők hatására csak úgy gyorsulhatnak, úgy mozoghatnak, hogy a mozgásuk folyamán a rendszer impulzusa állandó marad.
Jegyezzük meg a következőket. Először is az impulzusmegmaradás tétele nemcsak konzervatív, hanem minden fajta erőhatás fellépte esetén egyaránt érvényes. Másodszor, a (16) egyenlet vektor egyenlet lévén, tulajdonképpen nem egyetlen, hanem három skaláris egyenlettel egyenértékű, külön‐külön teljesül az impulzusvektor három komponensére, s így koordinátájára is. A bemutatott levezetéshez hasonlóan megnézhetjük azt az esetet is, ha a rendszerre külső erők is hatnak. Ilyenkor a tömegpontrendszer teljes impulzusának időegységre eső megváltozása egyenlő a külső erők vektori összegével. Ezért az impulzus megmaradása akkor is érvényes, ha hatnak külső erők, de azoknak eredője nulla. Ha pedig a mozgás folyamán csak a külső erők eredőjének valamely irányú összetevője marad nulla, akkor a rendszer impulzusvektorának ugyanezen irányú komponense marad állandó.

Az impulzusnyomaték megmaradási tétele

Egyetlen tömegpontnak valamely

O

pontra vonatkoztatott

N

impulzusnyomatékán a bevezetésben mondottak szerint a helyzetvektornak és az impulzusvektornak vektoriális szorzatát értjük (10. ábra):

\begin{matrix} N = r \times I = (r \times v) m . \end{matrix}

(17)

10. ábra

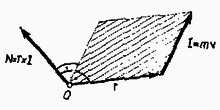Ha a tömegpont sebessége nem változik, vagyis a test egyenletes egyenes vonalú mozgást végez, nem változik a tömegpontnak bármely pontra vonatkozó impulzusnyomatéka sem. (L. a 11. ábrát és a 4. ábrával kapcsolatban mondottakat.)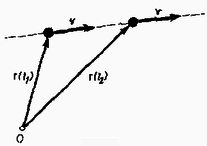

11. ábra

Az impulzusnyomatéknak kis

Δ t

idő alatt bekövetkező változása ezért csak a sebesség megváltozásának a következménye. Így

\begin{matrix} Δ N = (r \times Δ v) m = r \times Δ I = (r \times F) Δ t = M Δ t . \end{matrix}

(18)

Tehát az impulzus‐nyomaték megváltozása ugyanolyan kapcsolatban van a forgatónyomatékkal, mint az impulzus megváltozása az erővel.
A pontrendszer impulzus‐nyomatékán az egyes pontok impulzus‐nyomatékának vektori összegét értjük:

\begin{matrix} N = \sum r_{i} \times I_{t} = \sum m_{i} (r_{i} \times v_{i}) . \end{matrix}

(19)

Az impulzusnyomatékra használatos egyéb kifejezések: forgási impulzus, mozgásmennyiség-nyomaték, forgásmennyiség vagy perdület.
A pontrendszer impulzusnyomatékának megváltozása az egyes pontok impulzus‐nyomatékának megváltozásából tevődik össze, ezért

\begin{matrix} Δ N = \sum r_{i} \times Δ I_{t} = \sum M_{i} Δ t . \end{matrix}

(20)

Vagyis az impulzusnyomaték megváltozása arányos a forgató‐nyomatékok vektori összegével. Zárt rendszernél a belső erők forgatónyomatékának az összege azonban mindig nulla, miként azt pl, a 9. ábrán szemléltetett pontrendszernél közvetlenül láthatjuk (12. és 13. ábra).

12. ábra

13. ábra

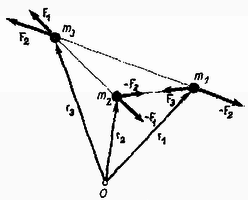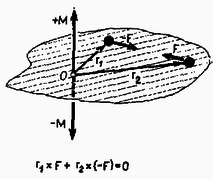Az erők ugyanis párosával lépnek fel, párosával ugyanabba a hatásvonalba esnek, de ellentétes irányúak, így bármely pontra forgatónyomatékuk is párosával egyenlő nagyságú de ellentétes irányú. Ezért zárt rendszernek a mozgása folyamán az ímpulzusnyomatéka is állandó marad. Ez az impulzusnyomaték megmaradási tétele. A levezetésből az is kitűnik, hogy a megmaradási tétel attól függetlenül igaz, hogy hol választjuk meg az

O

pontot. Természetesen az állandó

N

impulzus‐nyomaték maga, már (általában) függ a koordináta‐rendszer kezdőpontjának megválasztásától. Az impulzusnyomaték megmaradási tétele is vektor egyenlet, amely három skalár egyenlettel ekvivalens.
Hasonlóan az impulzusmegmaradás tételéhez, igaz az, hogy az impulzusnyomaték akkor is állandó marad, ha vannak külső erők, de azok forgatónyomatékának vektori összege nulla.
Előfordulhat az, hogy a külső forgatónyomatékok eredője csak bizonyos pontra (

O

-ra) vonatkozóan nulla, akkor csak az erre a pontra vonatkozó impulzusnyomaték marad állandó. Pl. amikor egyetlen tömegpont centrális erőtérben mozog, és az

O

pontot a centrumban vesszük fel, akkor a külső erőknek erre a pontra vonatkozó forgatónyomatéka nulla lesz, mivel az erő hatásvonala mindig keresztülmegy a középponton. Ezért erre a pontra:

\begin{matrix} m (r \times v) = állandó, \end{matrix}

(21)

és így állandótömeg esetén

\begin{matrix} \frac{1}{2} (r \times v) = állandó \end{matrix}

(22)

is teljesül, vagyis megkaptuk Kepler II. törvényét.
Az impulzusnyomaték természetesen akkor is lehet nullától különböző, ha az impulzus zérus. PL a 14. ábrán két ugyanakkora tömegű, ugyanakkora sugarú körpályán egymással szemben elhelyezkedő, függőleges tengely körül egyenletes körmozgást végző tömegpontból álló rendszer impulzusnyomatékát határoztuk meg.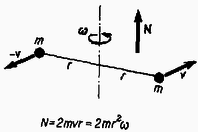

14. ábra

Ez az erőpárral analóg ,,impulzus-pár'' esete. Számítással meggyőződhetünk róla, hogy ebben az esetben az állandó forgásimpulzus nagysága is, iránya is a vonatkoztatási ponttól független. Iránya a forgástengellyel párhuzamos, nagysága pedig

\begin{matrix} N = 2 r m v = 2 m r^{2} ω . \end{matrix}

(23)

Vagyis az

m v

nagyságú impulzust szoroznunk kell az impulzuspár

2 r

,,karjával". Ebből a meggondolásból az is következik, hogy egy tengely körül forgómozgást végző pontok impulzusnyomatéka a koordináta‐rendszer kezdőpontjának megválasztásától független értékű akkor, ha a tömegpontok a tengelyre szimmetrikusan helyezkednek el.
A megismert megmaradási tételek segítségével számos fizikai feladatot meg tudunk oldani. Ehhez azonban nem elég maguknak a tételeknek az ismerete, hanem mindenkor ügyelnünk kell arra is, hogy megvizsgáljuk, teljesülnek-e a megmaradáshoz szükséges feltételek. Példaképpen nézzünk meg két feladatot ebből a szempontból.

m

tömegű pontszerű test

r

sugarú körpályán, mozogjon

ω

szögsebességgel (15. ábra).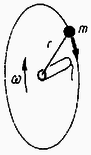

15. ábra

Kérdés az, hogy mekkora lesz a testnek a szögsebessége, ha a kötelet a kör középpontjában levő csapágyon keresztül meghúzva, a sugarat felére csökkentjük. A 16. ábrán hasonló mozgást ábrázoltunk, de itt a kötél egy vékony tengelyre csavarodik fel, és ezáltal rövidül meg.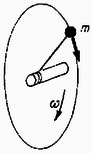

16. ábra

Kérdés, hogy mekkora lesz ebben az esetben a szögsebesség akkor, amikor a kötél fele már felcsavarodott. (A nehézségi erőtől mind a két esetben tekintsünk el.)
Az első esetben a megoldást az impulzusnyomaték megmaradásából kaphatjuk meg. A külső erő hatásvonala ugyanis keresztülmegy egy fix ponton, az eredeti kör középpontján, ezért az erre a pontra vonatkozó impulzusnyomaték megmarad:

\begin{matrix} N = r m v = m r^{2} ω = m {(\frac{r}{2})}^{2} ω_{x}, \end{matrix}

(24)

így

\begin{matrix} ω_{x} = 4 ω . \end{matrix}

(25)

A második esetben csak kényszererő hat. A kényszererő merőleges a pillanatnyi sebességre, így munkát nem végez, ezért most az energia marad állandó:

\begin{matrix} \frac{m}{2} v^{2} = \frac{m}{2} r^{2} ω^{2} = \frac{m}{2} {(\frac{r}{2})}^{2} ω_{x}^{2}, \end{matrix}

(26)

így most

\begin{matrix} ω_{x} = 2 ω . \end{matrix}

(27)

lesz.