Kezdőlap


Cím:	1969. évi Eötvös Loránd Fizikaverseny
Füzet:	1970/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat október 18-án rendezte ez évi fizikai versenyét. A versenyzők $5$ óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

M = 1, 5 \cdot 10^{25} gramm

tömegű,

R = 3600 km

rádiuszú égitest felszíne felett

h = 400 km

magasan egy űrhajó kering körpályán. Fékező rakétáját rövid ideig menetiránnyal szemben működtetve olyan ellipszispályára tért, amelyen az égitest átellenes pontján elérte annak felszínét. A fékezéskor mozgási energiájának hányadrészét kellett elvesztenie?

Megoldás. Jelöljük az

m

tömegű égitest sebességét a körpályán

v_{0}

-val. A tömegvonzási erő egyenlő a centripetális erővel:

\begin{matrix} \frac{m v_{0}^{2}}{R + h} = \frac{f M m}{{(R + h)}^{2}}; \end{matrix}

az űrhajó tömege kiesik és a körsebesség négyzete:

\begin{matrix} v_{0}^{2} = \frac{f M}{R + h} = \frac{f M}{R (1 + h / R)} . \end{matrix}

(1)

Ha az űrhajó ellipszispályára tér (1. ábra), akkor az ellipszis fél nagytengelye

a = R + h / 2

, excentricitása

c = h / 2

és fél kistengelye

b = R \sqrt[]{1 + h / R}

1. ábra

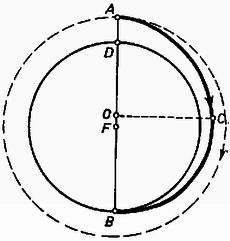Kepler III. törvénye szerint a keringési idők csak a fél nagytengelyektől függenek, a kistengelytől függetlenek. A körpályán

T_{0}

, az ellipszispályán

T

a keringési idő. Tehát

\begin{matrix} T^{2} : T_{0}^{2} = {(R + h / 2)}^{3} : {(R + h)}^{3} . \end{matrix}

A keringési idő az ellipszispályán:

\begin{matrix} T = T_{0} \sqrt[]{{(\frac{R + h / 2}{R + h})}^{3}} . \end{matrix}

A körpályán a keringési idő (1) felhasználásával:

\begin{matrix} T_{0} = \frac{2 π (R + h)}{v_{0}} = \frac{2 π (R + h) \sqrt[]{R + h}}{\sqrt[]{f M}} . \end{matrix}

Ezt felhasználva a keringési idő az ellipszispályán:

\begin{matrix} T = \frac{2 π {(R + h)}^{3 / 2}}{\sqrt[]{f M}} \cdot \frac{{(R + h / 2)}^{3 / 2}}{{(R + h)}^{3 / 2}} = \frac{2 π}{\sqrt[]{f M}} \cdot {(R + h / 2)}^{3 / 2} . \end{matrix}

Az ellipszis területe:

\begin{matrix} π a b = π (R + h / 2) \cdot R \cdot \sqrt[]{1 + h / R} . \end{matrix}

Ezeket felhasználva kiszámítjuk, mennyi a területi sebesség az egész ellipszispályából számítva:

\begin{matrix} \frac{π a b}{T} = \frac{\sqrt[]{f M} \cdot R \sqrt[]{1 + h / R}}{2 \sqrt[]{R + h / 2}} . \end{matrix}

(2)

Kepler II. törvénye szerint a területi sebesség az ellipszis minden pontján ugyanannyi. A fékezés

A

pontjában számítva a vezérsugár

R + h

és a sebesség valamilyen

v

. Ezekkel is kiszámíthatjuk a területi sebességet:

\begin{matrix} \frac{v (R + h)}{2} = \frac{v R (1 + h / R)}{2} . \end{matrix}

Ezt egyenlővé tesszük a (2) alatti területi sebességgel:

\begin{matrix} \frac{v R (1 + h / R)}{2} = \frac{\sqrt[]{f M} \cdot R \cdot \sqrt[]{1 + h / R}}{2 \sqrt[]{R + h / 2}} . \end{matrix}

Innen a fékezés pillanatában érvényes sebesség:

\begin{matrix} v = \frac{\sqrt[]{f M}}{\sqrt[]{1 + h / R} \cdot \sqrt[]{R + h / 2}}, \end{matrix}

és ennek a sebességnek a négyzete:

\begin{matrix} v^{2} = \frac{f M}{(1 + h / R) \cdot (R + h / 2)} . \end{matrix}

(3)

(1) és (3) összehasonlításával megkapjuk azt, hogy az

A

pontban történő fékezés után az eredeti mozgási energiának mekkora hányada maradt meg:

\begin{matrix} \frac{v^{2}}{v_{0}^{2}} = \frac{R}{R + h / 2} = \frac{2 R}{2 R + h} . \end{matrix}

Vagyis a mozgási energiák a nagytengelyek arányában állnak. A fékezéskor elvesztett mozgási energiahányad:

\begin{matrix} 1 - \frac{v^{2}}{v_{0}^{2}} = \frac{h}{2 R + h} . \end{matrix}

Az égitest tömege kiesik. A mi számadatainkkal az elvesztett energiahányad

1 / 19

2. A 2. ábra szerinti kapcsolásban

L_{a}

és

L_{c}

nagy önindukciójú tekercsek,

A

B

és

C

különböző ellenállású izzólámpák.

U

egyenfeszültség hosszabb ideje be van kapcsolva, a lámpák égnek. Vizsgáljuk meg a három izzólámpa viselkedését

K

kapcsoló kinyitása után!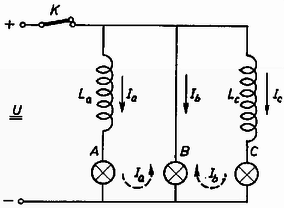

2. ábra

Megoldás. A kapcsoló működtetése előtt az egyes ágakban az izzólámpák ohmos ellenállásainak megfelelő

I_{a}

I_{b}

és

I_{c}

áramok folynak. A kapcsoló kinyitása után

I_{b}

áram azonnal megszűnik, hiszen ebben az ágban csak ohmos ellenállás volt. Az önindukciós tekercsek mágneses fluxusa az indukciótörvény szerint az első pillanatban nem változhat, ezért

I_{a}

és

I_{c}

áramok tovább folynak, mégpedig

B

izzólámpán át, alulról felfelé. Aszerint, hogy

I_{a} + I_{c}

az előbb még folyó

I_{b}

áramnál nagyobb, kisebb vagy egyenlő,

B

izzólámpa hirtelen felvillan, hirtelen elsötétül vagy változatlan fényű. Természetesen egy idő múlva az áramok megszűnnek.

2 R = 8 cm

átmérőjű,

f = 20 cm

gyújtótávolságú, gyűjtőlencse tengelyén egy pontszerű fényforrást és tőle

D = 50 cm

távolságban

2 r = 7 cm

átmérőjű kör alakú kartonlapot helyezünk el (a tengelyre merőlegesen). a) A lencse mely helyzetében lesz a kartonlap közepén a legerősebb a megvilágítás erőssége? b) Mikor lesz a legnagyobb a kartonlapra eső teljes fényenergia?

Megoldás. Először az a) kérdéssel foglalkozunk. Ez szükséges lehet abban az esetben, ha egy apró rést minél erősebben kell megvilágítanunk. A 3. ábra első rajza mutatja az elrendezést. A fényforrás és az ernyő

D

távolsága mindenképp állandó marad.

t

tárgy-lencse távolságot változtatjuk és

t

függvényeként vizsgálunk mindent. A fényforrás képe a lencsétől

k

távolságban keletkezne, ehelyett azonban az ernyőn kapunk

ϱ

rádiuszú megvilágított kört.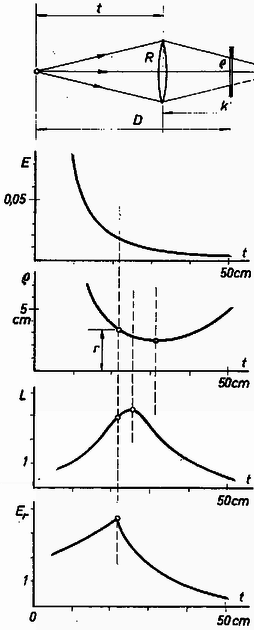

3. ábra

A lencse által hasznosított fényenergia azzal a kúpszöggel arányos, amelynek középpontja a fényforrásban van és a lencse határolja. Ezért (igen jó közelítéssel) a lencsét érő fényenergia arányos

R / t

négyzetével:

\begin{matrix} E = K {(\frac{R}{t})}^{2} . \end{matrix}

(4)

A lencsét érő

E

fényenergia

t

-től való függését mutatja a 3. ábra második rajza.
Hasonló háromszögekkel kiszámítjuk az ernyőn keletkező megvilágított kör

ϱ

rádiuszát:

\begin{matrix} \frac{ϱ}{R} = \frac{k + t - D}{k} . \end{matrix}

Felhasználva itt a lencsetörvényből adódó

k = t f / (t - f)

képtávolságot:

\begin{matrix} ϱ = R \cdot \frac{t^{2} - D t + D f}{t f} . \end{matrix}

(5)

Ennek a függvénynek a menetét a 3. ábra harmadik rajza mutatja.

ϱ

-nak minimuma van

t = \sqrt[]{D f} = 31, 6 cm

-nél, amikor

ϱ = 2, 7 cm

.
Ha az ernyőn keletkező megvilágítás erősségét keressük, akkor a (4) által rendelkezésre álló fényenergiát el kell osztanunk a

ϱ

rádiuszú kör területével:

\begin{matrix} L = \frac{E}{π ϱ^{2}} . \end{matrix}

Felhasználva

ϱ

-ra az (5) alatti eredményt, az ernyőn keletkező megvilágítási erősség:

\begin{matrix} L = \frac{K f^{2}}{π} \cdot \frac{1}{{(t^{2} - D t + D f)}^{2}} . \end{matrix}

(6)

Azonnal látható, hogy

L

-nek maximuma van ott, ahol a nevező a legkisebb. Ez

t = D / 2

-nél következik be. Tehát az a) kérdésre a felelet: a lencsét a fényforrás és ernyő távolságának közepére kell állítani, függetlenül a lencse fókusztávolságától. A megvilágítási erősségnek a lencsetávolságtól való függését a 3. ábra negyedik rajza mutatja. A megvilágítási erősség ezen maximumát beállítva az ernyőn megvilágított kör rádiusza

ϱ = 3 cm

, tehát a megvilágított kör nem tölti be az egész ernyőt. Egyébként az a) kérdésnél lényegtelen az ernyő nagysága.
Most vizsgáljuk meg a b) kérdést. Erre akkor lehet szükség, ha például fényt felfogó eszközünk egy fotocella és a legerősebb áramot akarjuk kapni.
Ha az (5) képletben

ϱ

helyébe

r

-et teszünk, akkor megtudjuk, mekkora

t

tárgytávolságnál tölti be a megvilágított kör éppen a felfogó ernyőt. A mi esetünkben

r = 3, 5 cm

és ennek alapján

t = 22 cm

mellett fér el a megvilágított kör éppen az ernyőnkön.
Mozgassuk el a lencsét balról jobbfelé, de induljunk el igen kis

t

-től, mondjuk

t = 10 cm

-től. Ekkor, egészen

t = 22 cm

-ig a megvilágított körnek csak egy része esik a felfogó ernyőre, ezért az ernyőre eső összes

E_{r}

fényenergiát az

L

-re kapott (6) alatti eredményünk és

π r^{2}

szorzata adja meg. Mivel a terület állandó, ezért egészen

t = 22 cm

-ig az összes fényenergia úgy növekszik, mint a 3. ábra negyedik rajzában

L

(lásd a 3. ábra ötödik rajzát). Ha a lencsével túlmegyünk

t = 22 cm

-en, akkor

ϱ

kisebbedik, az ernyő nincs egészen megtöltve fénnyel, tehát az ernyőre eső összes fényenergia úgy változik, minta lencsébe kerülő

E_{t}

energia. Ez azonban

t

távolság négyzetével fordított arányban csökken. Tehát ezekben a helyzetekben az összes fényenergia csökken. Így b) kérdésre a feleletünk: úgy kell a lencsét beállítani, hogy az ernyőn keletkező megvilágított kör éppen betöltse az ernyőt. A mi esetünkben ez

t = 22 cm

-nél következik be.

A verseny eredménye. I. díjat nyert Horváthy Péter, a budapesti Fazekas gimnázium IV. osztályos tanulója(tanára Mihály István). II. díjat nyert Lempert László, a budapesti Radnóti gimnázium IV. osztályos tanulója (tanára Kugler Sándorné). III. díjat nyert Nagy András, a budapesti Fazekas gimnázium III. osztályos tanulója (tanára Hutai Ferenc) és Láz József, a budapesti Eötvös gimnázium IV. osztályos tanulója (tanára Kellner Dénes). Dicséretet kapott Bajmóczy Ervin, a budapesti Fazekas gimnázium III. osztályos tanulója (tanára Hutai Ferenc), Gulyás András honvéd (a budapesti Apáczai Csere g.-ban Holics László volt tanítványa), Kálmán Péter, az ELTE fizikus hallgatója (a budapesti Apáczai Csere g-ban Holics László volt tanítványa) és Spitzer József honvéd (a budapesti Vörösmarty g.-ban Óhegyi Ernő volt tanítványa).