Cím: Egy töröttvonal tulajdonságairól
Szerző(k):  Siklósi István 
Füzet: 1970/május, 193 - 196. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Könnyű belátni, hogy ha egy irányított töröttvonal szakaszai egyenlők, és az egymás utáni szakaszok irányított α törésszögei egyenlők, akkor a töréspontok egy körön helyezkednek el (1. ábra), kivéve, ha α=0, illetve α=π, ugyanis ekkor a töréspontok egy egyenesen, illetve két pontban lesznek (2., illetve 3. ábra).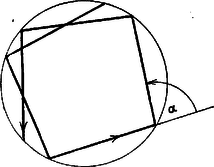

 
 
1. ábra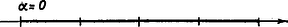
 
 
2. ábra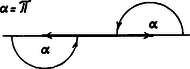
 
 
3. ábra
 

Tekintsünk most olyan, egyik irányban végtelen (a másik irányban véges) P1P2...Pn... töröttvonalat, melynek törésszögei szintén egyenlők, de bármely i=2, ..., n, ... indexre PiPi+1:Pi-1Pi=k, állandó és 0<k<1 (7. á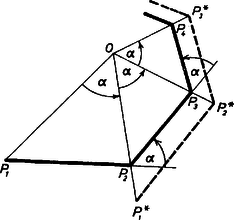bra).
 
 
7. ábra
 

Könnyű belátni, hogy ezen töröttvonal töréspontjaiból alkotott halmaznak az α=0, és az α=π esetben van egy és csak egy torlódási pontja* (4., illetve 5. ábra).
 
 
4. ábra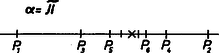
 
 
5. ábra
 

Bebizonyítjuk, hogy a töréspontok halmazának tetszőleges α mellett is egy és csak egy torlódási pontja van.
Elég azzal az esettel foglalkozni, amikor α konvex szög; ha ugyanis π<α<2π, akkor a töröttvonalat a sík tetszőleges egyenesére tengelyesen tükrözve olyan töröttvonalat kapunk, melyben a szakaszok hossza kielégíti a fenti feltételt, és a törésszögek konvex szögek lesznek (6. ábra).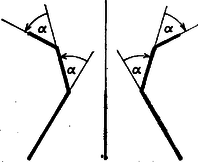
 
 
6. ábra
 

Ennek bizonyítására elég megjegyezni, hogy a tengelyes szimmetria távolság- és szögtartó, de az irányított szögek előjelét megváltoztatja. Legyen tehát 0<α<π.
Töröttvonalunk értelmezéséből következik, hogy a P1P2... és a P2P3... töröttvonalak hasonlók és a hasonlóság aránya 1:k. A két töröttvonal azonos körüljárású, tehát megfelelő elforgatással és nagyítással egymásba vihető (P1P2...-t visszük P2P3...-be). Az egymásba transzformálandó szakaszok törésszöge α, ezért az elforgatás szöge is α lesz, a nagyítás aránya pedig nyilván k (tulajdonképpen kicsinyítés).
Próbáljuk meg a transzformációt úgy végrehajtani, hogy a forgatás és a nyújtás centruma azonos legyen. Jelöljük az e körül elforgatott töröttvonalat P1*P2*...-gal. E célra olyan O pontot kell keresni, mely körül forgatva az O, P2, P1* és az O, P3, P2* ponthármasok egy-egy egyenesre esnek, ugyanis ekkor a nyújtással P1* a P2-be, P2* a P3-ba kerül, ..., tehát ez a transzformáció megfelel feltételeinknek.
Ha O olyan pont, hogy
P1OP2∢=P2OP3∢=α,(1)
akkor a forgatás után az O, P2, P1* és az O, P3, P2* ponthármasok valóban egy-egy egyenesen lesznek. (1)-et kielégítő O pont látókörök segítségével mindig szerkeszthető, tehát van olyan pont, mely körül elforgatva, majd ezen pontból mint centrumból vetítve, a P1P2... töröttvonal P2P3...-ba transzformálható.
Azt mutatjuk meg, hogy ez az O pont a töröttvonalnak torlódási pontja. Az elforgatás távolságtartó, a nagyítás aránya pedig k, tehát tetszőleges i mellett (i=1, 2, ... ) OPi+1:OPi=k, ebből
OPn:OP1=k⋅OPn-1:OP1=k2⋅OPn-2:OP1=...=kn-1⋅OP1:OP1=kn-1,
vagyis
OPn=kn-1⋅OP1.
0<k<1, és OP1 véges szám, tehát n növekedtével OPn→0, eszerint az O körül írt tetszés szerinti sugarú körben valóban van töröttvonalbeli töréspont. Ezzel állításunk első felének bizonyítását befejeztük.
Nyilvánvaló, hogy a torlódási pont akkor is létezik, ha a töröttvonal ugyanazokkal a tulajdonságokkal rendelkezik, mint eddig, de mindkét irányban végtelen. A továbbiakban ilyen töröttvonalakkal foglalkozunk. Ebben az esetben a 0<k<1 megszorítás sem szükséges, elegendő a 0<k≠1 kikötés. Bebizonyítjuk, hogy a töröttvonalnak csak egy torlódási pontja van.
A bizonyítást indirekt úton végezzük. Tegyük fel, hogy Q a töréspontok halmazának ‐ O-tól különböző torlódási pontja. Húzzunk Q középponttal olyan sugarú kört, hogy O a körön kívül essék. Vegyünk fel továbbá olyan, O középpontú körgyűrűt, mely tartalmazza a Q középpontú kört (8. ábra).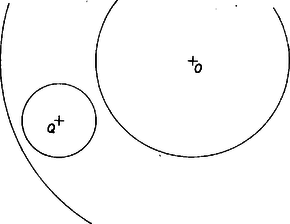
 
 
8. ábra
 

Két pozitív szám között egy mértani sorozatnak csak véges sok különböző tagja lehet (a hányados nem 1). Az OPi távolságok mind különbözőek és mértani sorozatot alkotnak, tehát a körgyűrűben legfeljebb véges sok töréspont helyezkedik el. A Q középpontú körben van Q-tól különböző töréspont, hiszen Q torlódási pont, de a töréspontok száma véges. Akkor viszont van közöttük olyan, melynek Q-tól mért távolsága a legkisebb. Az ennél a távolságnál kisebb sugarú, Q középpontú körben már nincs a Q-tól különböző töréspont, tehát Q nem lehet torlódási pont. Ezzel bebizonyítottuk, hogy a töröttvonalnak egy és csak egy torlódási pontja van.
Nézzük meg, milyen tulajdonságokkal rendelkezik ez a pont.
Rögzítsük a töröttvonal egy tetszés szerinti szakaszát (legyen ez P1P2), és k értékét. Bebizonyítjuk, hogy ha az α törésszög 0 és 2π között változik, akkor a torlódási pontok mértani helye egy kör.
A 0<α<π esetben láttuk, hogy OP1:OP2=k. Egy korábbi állításunk értelmében ez az arány a π<α<2π esetben is fennáll, és könnyen utánaszámolhatunk, hogy az α=0 és α=π esetben is igaz.
Ekkor viszont az O pont az úgynevezett Apollonius-féle körön helyezkedik el. Ezen kör minden pontja a mértani helyhez tartozik, hiszen a kör tetszőleges pontja meghatározza a P1OP2∢=α szöget, és az α törésszögű töröttvonal torlódási pontja éppen a körön kiválasztott pont lesz. Tehát a kérdéses mértani hely valóban egy kör (9. ábra).
 
 


Ha most a töröttvonal egy rögzített szakasza mellett a törésszög állandó és k értéke változik, akkor a torlódási pontok mértani helye egy körív a két végpont és a körív ívfelező pontja nélkül, illetve α=0 esetben két félegyenes a végpontok nélkül és α=π esetben egy szakasz a végpontok és a szakaszfelezőpont nélkül.
Állításunk következik abból, hogy P1OP2∢=α, tehát 0<α<π esetben O egy köríven helyezkedik el. (Azért nem két köríven, mert α irányított szög.) Ennek a körívnek azok a pontjai nem tartoznak a mértani helyhez, melyekre OP1:OP2=0, ∞, vagy 1 (10. ábra).
Ha π<α<2π, akkor az előző esetből P1P2 egyenesére való tükrözéssel nyerjük a megoldást.
α=0, illetve α=π esetben a P1P2 egyenesen helyezkednek el a torlódási pontok a P1P2 szakaszon kívül, illetve belül. Csak azok a pontok nem tartoznak a mértani helyhez, melyekre OP1:OP2=0, ∞, vagy 1 (11. ábra).
*Ponthalmaz torlódási pontjának olyan pontot nevezünk, mely körül írt tetszőleges sugarú körben ‐ magán a torlódási ponton kívül ‐ a ponthalmaznak legalább egy pontja helyezkedik el. (A torlódási pont nem feltétlenül eleme a ponthalmaznak.)