Kezdőlap


Cím:	Az 1969. évi (3.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1969/november, 161 - 165. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az 1. ábrán látható mechanikai rendszer három kocsiból áll, melyek tömege rendre $m_{A} = 0, 3 kg$ , $m_{B} = 0, 2 kg$ és $m_{C} = 1, 5 kg$ .
a) A $C$ kocsira olyan nagy $F$ erő hat vízszintesen, hogy az $A$ és $B$ kocsik $C$ -hez viszonyítva nyugalomban maradnak. Kiszámítandó az $A$ és $B$ kocsik közötti fonálban fellépő kötélerő és meghatározandó az $F$ erő.
b) Tegyük fel, hogy a $C$ kocsi nyugalomban van. Meghatározandó az $A$ és $B$ kocsi gyorsulása és a közöttük levő fonálban fellépő fonálerő.
Elhanyagolandók az összes súrlódási és közegellenállási erők, a fonál tömege, a csigák és a kocsikerekek tehetetlenségi nyomatéka.

1. ábra

Megoldás
a) Az

A

kocsi függőleges irányban nem gyorsul, ezért a kötelét

m_{A} g

erővel húzza. Ugyanez az erő húzza

B

-t is, amelynek gyorsulása

a_{B} = m_{A} g / m_{B}

, Ugyanekkora a három kocsiból álló rendszer gyorsulása is, tehát az

F

erő:

\begin{matrix} F = (m_{A} + m_{B} + m_{C}) \cdot \frac{m_{A}}{m_{B}} \cdot g . \end{matrix}

Számadatainkkal

a_{B} = a_{C} = 1, 5 g = 14, 7 {m / s}^{2}

, a fonálerő

2, 94 newton = 0,3 kp, F=29,4 newton=3 kp

.
b)

m_{A} g

gyorsító erő

m_{A} + m_{B}

tömeget gyorsít, ezért a gyorsulás:

\begin{matrix} \frac{m_{A}}{m_{A} + m_{B}} \cdot g = 0, 6 g = 5, 88 {m / s}^{2}, \end{matrix}

a fonálerő a súly és a gyorsító erő különbsége:

\begin{matrix} m_{A} g - m_{A} \cdot \frac{m_{A}}{m_{A} + m_{B}} \cdot g = \frac{m_{A} m_{B}}{m_{A} + m_{B}} \cdot g = 0, 12 kg\cdotg=1,176 newton=0,12 kp. \end{matrix}

Horváthy Péter

m_{1}

tömegű rézkaloriméterben

m_{2}

tömegű víz van, közös hőmérsékletük

t_{12}

. Egy

m_{3}

tömegű,

t_{3} < 0^{\circ} C

hőmérsékletű jégdarabot a kaloriméterben levő vízbe dobunk. Határozzuk meg az egyensúlyi közös hőmérsékletet a mennyiségek általános értékei mellett minden előforduló esetben. Az energiaveszteségeket hanyagoljuk el. A folyamat normális légnyomás mellett megy végbe. A réz fajhője

c_{1} = 0, 1 kcal/kg^{\circ} C

, a jég fajhője

c_{3} = 0, 5 kcal/kg^{\circ} C

, olvadási hője

L = 80 kcal/kg

. Vizsgáljuk meg ezt a numerikus esetet:

m_{1} = 1 kg

m_{2} = 1 kg

m_{3} = 2 kg

t_{12} = 10^{\circ} C

t_{3} = - 20^{\circ} C

. (A víz fajhője

c_{2} = 1 kcal/kg^{\circ} C

Megoldás. Ha a jeget bedobtuk a kaloriméter vizébe (2. ábra), akkor az egyensúly beállta után háromféle végállapothoz juthatunk: csak jég, csak víz, jég és víz van a kaloriméterben. Mindegyik esettel külön foglalkozunk.

2. ábra

a) A jég valamilyen (negatív)

t

hőmérsékletre melegszik fel, amihez

c_{3} m_{3} (t - t_{3})

kalória kell. Ezt a lehűlő kaloriméter és a víz fagyáshője adja:

\begin{matrix} c_{3} m_{3} (t - t_{3}) = c_{1} m_{1} (t_{12} - t) + c_{2} m_{2} t_{12} + m_{2} L - c_{3} m_{2} t . \end{matrix}

Innen az egyensúlyi hőmérséklet:

\begin{matrix} t = \frac{(c_{1} m_{1} + c_{2} m_{2}) t_{12} + c_{3} m_{3} t_{3} + m_{2} L}{c_{1} m_{1} + c_{3} m_{2} + c_{3} m_{3}} . \end{matrix}

(1)

De ez a képlet csak addig használható, amíg

t

negatívnak adódik. Eszerint az a) eset bekövetkezésének feltétele:

\begin{matrix} (c_{1} m_{1} + c_{2} m_{2}) t_{12} + c_{3} m_{3} t_{3} + m_{2} L < 0, \end{matrix}

illetőleg:

\begin{matrix} (c_{1} m_{1} + c_{2} m_{2}) t_{12} < - c_{3} m_{3} t_{3} - m_{2} L . \end{matrix}

(2)

(

t_{3}

sajátmaga mindig negatív.)
b) Átugorva a közbeeső lehetőséget most azt vizsgáljuk meg, ha az adatok olyanok, hogy az egyensúlyi hőmérséklet pozitív, a kaloriméterben végül csak víz van. A jég két lépésben történő felmelegítéséhez és megolvasztásához szükséges hőmennyiséget a lehűlő kaloriméter adja:

\begin{matrix} - c_{3} m_{3} t_{3} + m_{3} L + m_{3} t = (c_{1} m_{1} + c_{2} m_{2}) (t_{12} - t) . \end{matrix}

Innen az egyensúlyi hőmérséklet:

\begin{matrix} t = \frac{(c_{1} m_{1} + c_{2} m_{2}) t_{12} + c_{3} m_{3} t_{3} - m_{3} L}{c_{1} m_{1} + c_{2} m_{2} + m_{3}} . \end{matrix}

(3)

Ez a képlet csak akkor érvényes, ha

t

pozitívnak adódik, aminek feltétele:

\begin{matrix} - c_{3} m_{3} t_{3} + m_{3} L < (c_{1} m_{1} + c_{2} m_{2}) t_{12} . \end{matrix}

(4)

c) Most foglalkozunk azzal a középső esettel, amikor a beálló egyensúly-állapotban víz és jég egymás mellett van a kaloriméterben. Ekkor biztosan

t = 0^{\circ} C

. (2) és (4) egybevetésével rögtön látszik, hogy ennek az esetnek a feltétele:

\begin{matrix} - c_{3} m_{3} t_{3} + m_{3} L < (c_{1} m_{1} + c_{2} m_{2}) t_{12} < - c_{3} m_{3} t_{3} - m_{2} L . \end{matrix}

(5)

(Azt is megfigyelhetjük, hogy azokban a határesetekben, amikor (2)-ben és (4)-ben egyenlőségjelet írunk, (1) és (3)

t

számára

0

-t ad.) Ebben a b) esetben arra vagyunk kíváncsiak, mennyi jég és víz lesz a kaloriméterben. A lehűlő kaloriméter

(c_{1} m_{1} + c_{2} m_{2}) t_{12}

hőmennyiséget ad le. Lehet, hogy ebből a jég

0^{\circ}

-ra való felmelegítésén kívül még

m_{x}

gramm jég megolvasztására is jut:

\begin{matrix} (c_{1} m_{1} + c_{2} m_{2}) t_{12} = - c_{3} m_{3} t_{3} + m_{x} L \end{matrix}

és így a megolvasztott jég mennyisége:

\begin{matrix} m_{x} = \frac{(c_{1} m_{1} + c_{2} m_{2}) t_{12} + c_{3} m_{3} t_{3}}{L} . \end{matrix}

De az is lehetséges, hogy a vízből

m_{x}

gramm hozzáfagy a jéghez és csak így képes a közös

0^{\circ}

létrejönni:

\begin{matrix} (c_{1} m_{1} + c_{2} m_{2}) t_{12} + m_{y} L = - c_{3} m_{3} t_{3}, \\ m_{y} = \frac{- (c_{1} m_{1} + c_{2} m_{2}) t_{12} - c_{3} m_{3} t_{3}}{L} . \end{matrix}

A kaloriméterben végül is megtalálható víz mennyiségére mindegyik esetben egyformán ugyanaz a képlet következik:

\begin{matrix} m_{v} = m_{2} + m_{x} = m_{2} - m_{y} = m_{2} + \frac{(c_{1} m_{1} + c_{2} m_{2}) t_{12} + c_{3} m_{3} t_{3}}{L} . \end{matrix}

Látjuk: aszerint, hogy

(c_{1} m_{1} + c_{2} m_{2}) t_{12}

nagyobb, kisebb vagy egyenlő

c_{3} m_{3} t_{3}

abszolút értékéhez képest, aszerint olvad jég, hozzáfagy víz vagy mennyiségük az eredeti marad. A jég végső mennyisége

m_{j} = m_{2} + m_{3} - m_{v}

.
Feladatunk számadatai mellett

(c_{1} m_{1} + c_{2} m_{2}) t_{12} = 11 kcal

c_{3} m_{3} t_{3} = - 20 kcal

- c_{3} m_{3} t_{3} + m_{3} L = 180 kcal

- c_{3} m_{3} t_{3} - m_{2} L = - 60 kcal

, tehát (5) szerint a b) esetről van szó, a hőmérséklet

t = 0^{\circ}

m_{v} = 0,8875 kg

m_{j} = 2,1125 kg

, a hozzáfagyás esete.

Maróti Péter

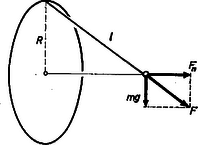
3. Függőleges síkban elhelyezett drótkarika rádiusza

R = 5 cm

. A karika legfelső pontjához erősített szigetelő fonálon

m = 1 gramm

tömegű kis golyó lóg. Az egész karikának, azonkívül a golyónak

Q = 9 \cdot 10^{- 8} coulomb

egyező előjelű elektromos töltéseket adtunk és azt tapasztaltuk, hogy kitérítés után a golyócska éppen a karika síkjára merőleges szimmetriatengelyben helyezkedik el. Milyen hosszú a fonál?

Megoldás. Ha a drótkarika töltése egyetlen pontban volna összpontosítva, akkor az erő Coulomb törvénye szerint

F = k Q^{2} / l^{2}

lenne. A mi esetünkben a karika minden egyes részéről okozott erő nem esik a szimmetriatengelybe, hanem vele egyező szögeket zár be (3. ábra).

3. ábra

A kimozdítás szempontjából az

F

erők vízszintes vetületére van szükségünk, ezeknek az összege

(F_{n})

, tekintettel a szimmetrikus helyzetre úgy számítható, mintha az előbbi

F

erő vetületét keresnénk. Tekintettel a hasonló háromszögekre a súlyerő és

F

aránya

R / l

\begin{matrix} \frac{R}{l} = \frac{m g}{F} = \frac{m g}{k Q^{2} / l^{2}} . \end{matrix}

Innen a fonálhossz:

l = \sqrt[3]{\frac{R k Q^{2}}{m g}}

. Ha a Coulomb-törvényben newtont, coulombot és métert használunk, akkor az arányossági szorzó

k = 9 \cdot 10^{9}

és a feladat számadataival a fonálhossz

l = 7, 2

centiméter.

Kálmán Péter

2 cm

élhosszúságú üvegkocka fölé üveglemezt helyezünk úgy, hogy a lemez és a kocka között vékony planparalel levegőréteg maradjon. A lemezre merőlegesen

0, 4 μ

-tól

1, 15 μ

-ig terjedő hullámhosszúságú elektromágneses hullámokat ejtünk és ezek a levegőréteg mindegyik oldalán visszaverődve interferálnak. Ebben a hullámhossztartományban csak két hullámhosszra teljesül az interferenciamaximum feltétele. Az egyiknél a hullámhossz

λ_{1} = 0, 4 μ

. Milyen vastag a levegőréteg?

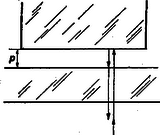4. ábra

Megoldás. A

d

vastagságú levegőrétegben (4. ábra) a fény útja oda és vissza

2 d

hosszúságú. Figyelembe véve, hogy az üvegrétegen való visszaverődéskor

180^{\circ}

-os fáziskésés következik be, az adott

λ_{1}

hullámú fény számára az erősítés feltétele:

\begin{matrix} 2 d = k_{1} λ_{1} + \frac{λ_{1}}{2}, ahol k_{1} = 0,1,2,3, ... . \end{matrix}

Ugyanígy a másik erősítést adó hullámhossz esetében:

\begin{matrix} 2 d = k_{2} λ_{2} + \frac{λ_{2}}{2}, ahol k_{2} = 0,1,2,3, ... . \end{matrix}

A két feltétel összehasonlításából következik, hogy

\begin{matrix} \frac{2 k_{1} + 1}{2 k_{2} + 1} = \frac{λ_{2}}{λ_{1}} . \end{matrix}

Tekintettel a megadott hullámhossz-tartományra,

λ_{2} / λ_{1} = 1, 15 / 0, 4 = 2, 875

lehet a két hullámhossz arányának legnagyobb értéke. Ugyanakkor az arány legkisebb értéke

1

. Így adódik az első feltétel:

\begin{matrix} 1 < \frac{2 k_{1} + 1}{2 k_{2} + 1} < 2, 875. \end{matrix}

(6)

Fel kell használnunk a feladat azon kikötését, hogy csak két hullámnál teljesül a megadott intervallumban a maximum feltétele. A (6) egyenlőtlenség bal oldala mutatja, hogy

k_{1} > k_{2}

. A feladat szerint csak egyetlen

k_{1}

és

k_{2}

van megengedve. Ha tehát

k_{1}

megfelel, akkor

k_{2} = k_{1} - 1

-nek is meg kell felelni, de

k_{2} = k_{1} - 2

-nek már nem szabad megfelelni. Ha ugyanis megfelelne például

k_{2} = k_{1} - 3

is, akkor szükségképp megfelelne

k_{1} - 1

k_{1} - 2

is, mert ezek is egész számok. De ez tilos. Felírjuk a (6) egyenlőtlenség jobb oldalával, hogy

k_{1} - 1

megfelel, de

k_{1} - 2

nem felel meg:

\begin{matrix} A_{1} = \frac{2 k_{1} + 1}{2 (k_{1} - 1) + 1} < 2, 875, & (7) \\ A_{2} = \frac{2 k_{1} + 1}{2 (k_{1} - 2) + 1} > 2, 875. & (8) \end{matrix}

Kipróbáljuk

A_{1}

és

A_{2}

értékeit

k_{1}

néhány egészszámú értékénél:

\begin{matrix} \begin{matrix} k_{1} & 0 & 1 & 2 & 3 & 4 & ... \\ A_{1} & - 1 & 3 & 1,67 & 1,4 & 1,28 & ... \\ A_{2} & - 0,33 & - 3 & 5 & 2,33 & 1,8 & ... \end{matrix} \end{matrix}

Látható, hogy (7)-nek megfelel minden

k_{1} ≧ 2

, de (8)-nak csak

k_{1} = 2

felel meg. Tehát a

λ_{1}

hullámhosszú fény interferenciájának rendje

k_{1} = 2

, a

λ_{2}

-es fényé

k_{2} = 1

.
Kiinduló egyenletünkből most könnyen következik, hogy

2 d = 2 \cdot 0, 4 + 0, 2 = 1 μ

és a levegőréteg keresett vastagsága

d = 0,5 μ

. A másik hullámhossz

2 \cdot 0, 5 = 1 \cdot λ_{2} + \frac{λ_{2}}{2}

alapján

λ_{2} = 0, 667 μ

.
A feladat eredeti szövege szerint az is számítandó volt, hogy az üvegkocka

8 \cdot 10^{- 6} {f o k}^{- 1}

értékű lineáris hőkiterjedési együtthatója mellett hány fokos melegedés szükséges ahhoz, hogy az üvegkocka alulról hozzáérjen az üveglemezhez és megszűnjön az interferáló levegőréteg. A számítás szerint ehhez kb.

3^{\circ}

-os melegedés elegendő, ami arra figyelmeztet, hogy kényes optikai kísérleteknél milyen fontos a hőmérséklet állandósága.

Spitzer József

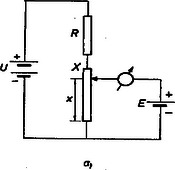
5. Gyakorlati feladat. Adva van áramforrás (két sorba kötött, elhanyagolható belső ellenállású NiFe akkumulátor), ismert

R

ellenállású ellenállásszekrény és

X

ismeretlen ellenállású mérődrót sorbakapcsolásával készült zárt áramkör. A mérődróton csúszó érintkező, mellette milliméterskála van. Egy szárazelemből és galvanométer-nulleszközből álló áramkört úgy kell az előbbi áramkörhöz hozzákapcsolni, hogy a nulleszközön ne folyjon áram. Meghatározandó a szárazelem és az akkumulátortelep kapocsfeszültségének hányadosa. Meghatározandó a mérődrót ismeretlen

X

ellenállása.
Megoldás. A kapcsolás két lehetőségét az 5. ábra a) és b) rajza mutatja.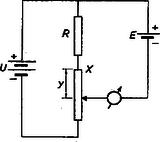

b. ábra

5. ábra

R + X

ellenállások egy feszültségosztót alkotnak, amelynek egyik vagy másik végéről levehetjük az elem

E

elektromotoros erejével egyező feszültséget. A helyes beállításnál nem folyik áram, tehát az elektromotoros erőt mérjük (kompenzációs feszültségmérés). Az a) szerint végzett kísérletnél a nulleszköz helyes beállításakor a csúszó érintkező a mérődrót alsó végétől számítva

x

törtrésszel kifejezett helyzetben áll

(0 < x < 1)

. A szárazelem

E

elektromotoros erejének és az akkumulátortelep

U

feszültségének aránya egyenlő az ellenállások arányával:

\begin{matrix} \frac{E}{U} = \frac{x X}{R + X} . \end{matrix}

A b) elrendezés szerint is megkeressük azt a helyzetet, amikor a null-eszköz nem jelez áramot. Ez a csúszó érintkező felülről számított

y

törtrészénél valósult meg

(0 < y < 1)

. A feszültségek aránya most:

\begin{matrix} \frac{E}{U} = \frac{R + y X}{R + X} . \end{matrix}

Két egyenletünk egyenletrendszert alkot

E / U

és

X

ismeretlenekkel. Az egyenletrendszer megoldása adja a feleletet a feltett kérdésekre:

\begin{matrix} \frac{E}{U} = \frac{x}{1 + x - y}, X = R \cdot \frac{1}{x - y} . \end{matrix}

Andor László