Cím:	Az 1969. évi fizika OKTV feladatai
Füzet:	1969/október, 81 - 86. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. forduló feladatai   1. $7\text{kg}$ tömegű láda vízszintes lapon nyugszik. A ládához kötött, csigán átvetett fonál végére $3\text{kg}$-os tömeget akasztunk. Ennek elengedése után $2$ másodperc múlva a fonalat elégetjük. Mekkora utat tesz meg a láda ? Hol van a leszakadt súly a láda megáldásának pillanatában ? (A láda és a súly mozgása számára a szükséges úthosszak rendelkezésre állnak.) A súrlódási együttható a sebességtől függetlenül $0\mathrm{,}2$.   Megoldás. A lehetséges legnagyobb súrlódási erő $0\mathrm{,}2\cdot 7\text{kp=1,4 }\text{kp=13,72}$ newton. Ez működésbe lép, mert a láda mozog. A mozgató erő $\left(3-1\mathrm{,}4\right)\text{<span style="font-weight: normal;font-style: normal;">kp</span>}=1\mathrm{,}6\text{<span style="font-weight: normal;font-style: normal;">kp</span>}=15\mathrm{,}68\text{<span style="font-weight: normal;font-style: normal;">newton</span>}$, a mozgatott tömeg $10\text{<span style="font-weight: normal;font-style: normal;">kg</span>}$, ezért a keletkező gyorsulás $a=F:m=15\mathrm{,}68\text{<span style="font-weight: normal;font-style: normal;">N</span>}:10\text{<span style="font-weight: normal;font-style: normal;">kg</span>}=1\mathrm{,}568\text{<span style="font-weight: normal;font-style: normal;">m/s</span>}2$. A második másodperc végén a sebesség $v=at=3\mathrm{,}136\text{<span style="font-weight: normal;font-style: normal;">m/s</span>}$, az addig megtett út $s=a{t}^2/2=3\mathrm{,}136\text{m}$ (1. ábra).     1. ábra   A fonál elégetése után a ládát a súrlódási erő fékezi, a fékező gyorsulás , a fékezés ideje $t=v/a=3\mathrm{,}136:1\mathrm{,}96=1\mathrm{,}6\text{s}$. Ezalatt a láda útja s$=1\mathrm{,}96\cdot 1\mathrm{,}{6}^2/2=2\mathrm{,}509\text{<span style="font-weight: normal;font-style: normal;">m</span>}$; a láda összes útja $3\mathrm{,}136\text{m+2,509 }\text{m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>≈</mo></math>5,65 }\text{m}$. A súly a fonál elégetésének a pillanatától kezdve függőleges lefelé hajítást végez $3\mathrm{,}136\text{m/s}$ kezdősebességgel. Ennek útja $1\mathrm{,}6\text{<span style="font-weight: normal;font-style: normal;">s</span>}$ alatt $s=3\mathrm{,}136\cdot 1\mathrm{,}6+4\mathrm{,}9\cdot$ $\cdot 1\mathrm{,}62\approx 17\mathrm{,}6\text{m}$.   2. Egy tartályban víz van és ezen $10\text{cm}$ vastagságú, ${\gamma }_0=0\mathrm{,}5\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>p</mi><mo stretchy="false">/</mo><mi>c</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$ fajsúlyú deszka úszik. A csövön át $100$ atmoszféra nyomású levegőt nyomunk be a tartályba. Milyen mélyen merül be a deszka ? (Tekintsük a vizet összenyomhatatlannak. A hőmérséklet nem változik.) A levegő fajsúlya $1$ atmoszféra nyomáson $0\mathrm{,}0013\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>p</mi><mo stretchy="false">/</mo><mi>c</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$.   Megoldás. Két közeg határfelületén történő úszásról van szó (2. ábra). 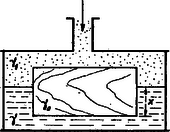    2. ábra   Legyen $x$ a folyadékba merülő rész magassága, $d$ a deszka vastagsága és $\gamma$ a folyadék fajsúlya. A levegő fajsúlya ${\gamma }_1=100\cdot 0\mathrm{,}0013=0\mathrm{,}13\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>p</mi><mo stretchy="false">/</mo><mi>c</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$, mert a fajsúly arányos a nyomással. Az alapterület legyen $A$. A deszka súlya egyenlő a folyadékba és a gázba merülő részek felhajtóerőinek összegével: $\begin{array}{c}{\displaystyle Ax\gamma +A\left(d-x\right)\cdot {\gamma }_1=Ad{\gamma }_0\mathrm{.}}\end{array}$ Innen a folyadékba merülő rész magassága: $\begin{array}{c}{\displaystyle x=d\cdot \frac{{\gamma }_0-{\gamma }_1}{\gamma -{\gamma }_1}=10\text{<span style="font-weight: normal;font-style: normal;">cm</span>}\cdot \frac{0\mathrm{,}5-0\mathrm{,}13}{1-1\mathrm{,}13}=4\mathrm{,}25\text{cm. }}\end{array}$ 3. 4 méter átmérőjű, belül üres félgömb átellenes felső pontjairól $m_1=3\text{kg}$-os és $m_2=2\text{kg}$-os tömegeket egyszerre engedünk el. Ütközésük teljesen rugalmas. Mekkora magasságot érnek el a testek az első ütközés után ? A súrlódás elhanyagolandó.   Megoldás. A két test egyszerre, egyformán $v=\sqrt[]{2gr}$ sebességgel érkezik a félgömb aljára (3. ábra). 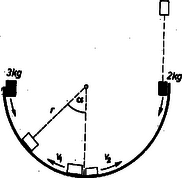    3. ábra   Itt rugalmas ütközés megy végbe, melynek folyamán az impulzus is, a mozgási energia is állandó marad. A rugalmas ütközés ismert képleteivel az ütközés utáni sebességek: $\begin{array}{c}{\displaystyle v_1=-0\mathrm{,}6v\mathrm{,}{v}_2=1\mathrm{,}4v\mathrm{.}}\end{array}$ A balra irányuló sebességet számítottuk negatívnak. A 3 kg-os tömeg ezzel a $v_1$ sebességgel $m_{1}g{h}_1=m_1{v}_1^2/2$ alapján $h_1=0\mathrm{,}36r=0\mathrm{,}72$ méter magasságig fut fel a félgömb belsejében. A 2 kg-os tömeg $v_2$ sebességével $m_{2}g{h}_2=m_2{v}_2^2/2$ szerint $h_2=1\mathrm{,}96r=3\mathrm{,}92$ méter magasságig jut fel, ami azt jelenti, hogy a félgömb pereme fölé még $0\mathrm{,}96r=1\mathrm{,}92$ méter magasságig felrepül függőlegesen.   A II. forduló feladatai   1. ${30}^{\circ }$-os hajlásszögű lejtő $R=2$ méter sugarú, függőleges síkú körpályához törés nélkül csatlakozik. A lejtőről $h=2R$ magasságból $r=1\text{<span style="font-weight: normal;font-style: normal;">cm</span>}$ sugarú, $m=20$ gramm tömegű golyót engedünk el (4. ábra).     4. ábra   Legalábbis mekkora súrlódási együtthatóra van szükség, hogy a golyó csúszás nélkül guruljon végig ? (Nagy László)   Megoldás. Először vizsgáljuk meg, mi a feltétele annak, hogy $\beta$ hajlásszögű lejtőn egy golyó megcsúszás nélkül, simán guruljon le (5. ábra). 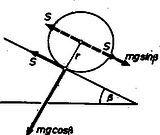    5. ábra   A golyót a lejtő mentén $mg\text{sin}\beta$ viszi lefelé, de az érintkezési pontban $S$ súrlódási erő hat felfelé. A golyó középpontjában hozzáveszünk $\pm S$ erőt. Közülük a felfelé ható erőt összegezzük az $mg\text{sin}\beta$ erővel. A golyó középpontja $a$ állandó gyorsulással mozog lefelé, a mozgató erő: $\begin{array}{c}{\displaystyle ma=mg\text{sin}\beta -S\mathrm{.}}\end{array}$ (1) A golyót ezenkívül még $Sr$ forgatónyomatékú erőpár forgatja. Mivel a szöggyorsulás egyenlő a forgatónyomaték és tehetetlenségi nyomaték hányadosával, ezért $Sr$ forgatónyomaték $\Theta$ tehetetlenségi nyomaték mellett $Sr/\Theta$ szöggyorsulást okoz. A szöggyorsulást $r$ rádiusszal szorozva a kerületmenti gyorsulást kapjuk meg: $\begin{array}{c}{\displaystyle a=\frac{S{r}^2}{\Theta }\mathrm{.}}\end{array}$ (2) Az (1) és (2)-ből álló egyenletrendszer megoldása szolgáltatja a golyó haladó mozgásának $a$ gyorsulását és a működő $S$ súrlódási erőt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a=g\text{sin}\beta \cdot \frac{m{r}^2}{\Theta +m{r}^2}\mathrm{,}}& \text{(<mn>3</mn>)}\\ \hfill {\displaystyle S=mg\text{sin}\beta \cdot \frac{\Theta }{\Theta +m{r}^2}\mathrm{.}}& \text{(<mn>4</mn>)}\end{array}}$ (L. egyébként a Lapok 1965. évi 6.számának 43. oldalát.) Feladatunkban egy körpálya belsejében felszaladó golyóról van szó (6. ábra). 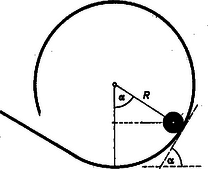    6. ábra   Határozza meg a golyó helyzetét a hozzávezető $R$ rádiusznak a függőlegessel alkotott $\alpha$ szöge. Ebben a helyzetben a golyó pillanatnyilag $\alpha$ hajlásszögű lejtőn van, rá alkalmazhatók a (3) és (4) eredmények, természetesen $\beta$ helyébe $\alpha$-t téve. A golyó akkor mozog megcsúszás nélkül, ha a mozgásához szükséges súrlódási erő nem lépi túl azt az értéket, amely az adott súrlódási együttható mellett maximálisan keletkezhet. Ezért most megvizsgáljuk $\alpha$ függvényében mindkettőt. A sima legördülés alkalmával szükséges súrlódási erő a golyó $\alpha$ szöggel jellemzett helyzetében (4) alapján: $\begin{array}{c}{\displaystyle S=mg\text{sin}\alpha \cdot \frac{\Theta }{\Theta +m{r}^2}\mathrm{.}}\end{array}$ (5) A maximálisan keletkezhető súrlódási erő számítása céljából szükségünk van arra az erőre, amely a golyót a merőlegesen kifelé nyomja a rádiusz irányában. Ez az erő az $mg\text{cos}\alpha$ lejtőmenti súlyösszetevőnek és $m{v}^2/R$ centrifugális erőnek az összege: $\begin{array}{c}{\displaystyle F_n=mg\text{cos}\alpha +\frac{m{v}^2}{R}\mathrm{.}}\end{array}$ A kérdéses $\alpha$ helyzetben meglevő $v$ sebességet az energiamegmaradás törvényével számítjuk. $m{v}^2/2$ haladásból származó mozgási energia mellett az $\omega$ szögsebességgel forgó golyónak $\Theta {\omega }^2/2=\Theta v^2/2r^2$ forgási energiája is van. A lesüllyedés magassága $h-R+R\text{cos}\alpha$, ha $r$-et elhanyagoljuk a sokkal nagyobb $R$ mellett. Az energia megmaradása alapján: $\begin{array}{c}{\displaystyle mg\left(h-R+R\text{cos}\alpha \right)=\frac{m{v}^2}{2}+\frac{\Theta v^2}{2r^2}\mathrm{.}}\end{array}$ Ebből az egyenletből a sebesség négyzete mint $\alpha$ függvénye: $\begin{array}{c}{\displaystyle v^2=2g\left(h-R+R\text{cos}\alpha \right)\cdot \frac{m{r}^2}{\Theta +m{r}^2}\mathrm{.}}\end{array}$ Ezt behelyettesítjük $F_n$ merőlegesen a falhoz nyomó erő előbbi kifejezésébe; összevonás után: $\begin{array}{c}{\displaystyle F_n=mg\left[2\left(\frac{h}{R}-1\right)\cdot \frac{m{r}^2}{\Theta +m{r}^2}+\frac{\Theta +3m{r}^2}{\Theta +m{r}^2}\cdot \text{cos}\alpha \right]\mathrm{.}}\end{array}$ (6) Ezt az $F_n$-t $\mu$ súrlódási együtthatóval megszorozva kapjuk a lehetséges legnagyobb súrlódási erőt: $\mu F_n$. Ha azt akarjuk, hogy a golyó ne csússzék meg, akkor $\mu F_n$, legalább is egyenlő kell, hogy legyen az (5) által megadott súrlódási erővel. (6) felhasználásával: $\begin{array}{c}{\displaystyle mg\text{sin}\alpha \cdot \frac{\Theta }{\Theta +m{r}^2}=\mu mg\left[2\left(\frac{h}{R}-1\right)\cdot \frac{m{r}^2}{\Theta +m{r}^2}+\frac{\Theta +3m{r}^2}{\Theta +m{r}^2}\cdot \text{cos}\alpha \right]\mathrm{.}}\end{array}$ Ebből kifejezzük, miként függ a szükséges $\mu$ súrlódási együttható a golyó $\alpha$ szöggel jellemzett helyzetétől: $\begin{array}{c}{\displaystyle \mu =\frac{\text{sin}\alpha }{2\left(\frac{h}{R}-1\right)\frac{m{r}^2}{\Theta }+\left(1+\frac{3m{r}^2}{\Theta }\right)\text{cos}\alpha }\mathrm{.}}\end{array}$ (7) A (7) alatti függést a 7. ábra mutatja. 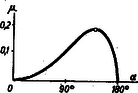    7. ábra   A függvény maximuma, tehát a legnagyobb szükséges súrlódási együttható azon ${\alpha }_k$ szögnél van, amelyre $\begin{array}{c}{\displaystyle \text{cos}{\alpha }_k=-\frac{3+\frac{\Theta }{m{r}^2}}{2\left(\frac{h}{R}-1\right)}\mathrm{.}}\end{array}$ ${}^{*}$ Felhasználva ezt az értéket (7)-ben, a szükséges legnagyobb súrlódási együttható: $\begin{array}{c}{\displaystyle {\mu }_k=\frac{\Theta }{\sqrt[]{4{\left(m{r}^2\right)}^2{\left(\frac{h}{R}-1)\right)}^2-{\left(\Theta +3m{r}^2\right)}^2}}}\end{array}$ Feladatunk számadatait felhasználva $\Theta =2m{r}^2/5$, $h/R=3$ és így a (7) szerinti súrlódási együttható: $\begin{array}{c}{\displaystyle \mu =\frac{\text{sin}\alpha }{10+8\mathrm{,}5\text{cos}\alpha };}\end{array}$ $\text{cos}{\alpha }_k=-17/20=-0\mathrm{,}\mathrm{85,}{\alpha }_k=148\mathrm{,}{2}^{\circ }$ és a szükséges legnagyobb súrlódási együttható: $\begin{array}{c}{\displaystyle {\mu }_k=\frac{2}{\sqrt[]{111}}=0\mathrm{,}1898.}\end{array}$ Meg kell vizsgálni, hogy az a súrlódási együttható elegendő-e a $\beta ={30}^{\circ }$-os leszaladó lejtőn a sima gördüléshez. (4) alapján megvizsgálva gömbnél a $\beta$ szögű lejtőn legalább 2 tg $\beta /7=0\mathrm{,}165$ értékű súrlódási együttható szükséges. Ennél 0,1898 nagyobb, tehát a lejtőn is sima gördülés van.   2. Hosszú $U$ alakú cső mindegyik szárában egyenlő magasan áll a higany. Az egyik szár nyitott, a másik zárt. A cső keresztmetszet területe $2\mathrm{,}5\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>c</mi><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$, a jobb oldali szárban elzárt légoszlop hossza $40\text{cm}$. A higany fajsúlya $13\mathrm{,}6\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>p</mi><mo stretchy="false">/</mo><mi>c</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$. Ezután a nyitott csővéget súrlódásmentes dugattyúval elzárjuk és erre a dugattyúra $1190\text{pond}$os súlyt helyezünk. Az új egyensúly beállta után hogyan helyezkednek el a higanyfelszínek ?   Megoldás. Célszelű a nyomásokat higanyoszlop-cm-ben számítani (8. ábra). 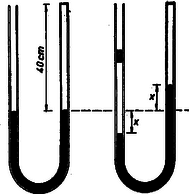    8. ábra   Tekintet nélkül a bal oldali légoszlop hoszszára, a 76 Hgcm légnyomáshoz a dugattyú folytán hozzáadódó nyomás $1190/\left(2\mathrm{,}5\cdot 13\mathrm{,}6\right)=35$ Hgcm. Eszerint a bal oldali higanyfelszínen a nyomás $76+35=111$ Hgcm. Emiatt a higanyfelszínek $x$ cm-rel mozdultak el. A nyomás a zárt csőben a higanyfelszín tetején $(111-$ $-2x)$ Hgcm. Alkalmazzuk Boyle‐Mariotte törvényét a jobb oldali csőben elzárt levegőre: $\begin{array}{c}{\displaystyle 2\mathrm{,}5\cdot 40\cdot 76=2\mathrm{,}5\left(40-x\right)\left(111-2x\right)\mathrm{.}}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle 2x^2-191x+1400=0.}\end{array}$ Ennek megoldása: $x_1=87\mathrm{,}5\text{cm}$, $x_2=8\text{cm}$. Ez a második gyök használható, tehát a higanyfelszínek 8 cm-t mozdultak el lefelé és felfelé.   3. $f=4\text{cm}$-es gyújtótávolságú, kör alakú, vékony gyűjtőlencse közepén egy kör alakú lyuk van, amelynek átmérője a lencse átmérőjének fele. Egy faltól $A=9\text{cm}$ távolságban pontszerű fényforrás van. Hová helyezzük a lencsét, hogy a falon egyetlen, kívül élesen határolt megvilágított kör keletkezzék ?   Megoldás. A lyuk határán átmenő sugárkúp az ernyőt $h$ rádiuszú körben metszi (9. ábra). 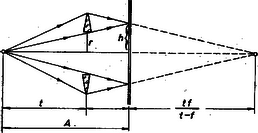    9. ábra   A fényforrást leképező, a lencse külső szélén áthaladó fénysugaraknak ugyanezt a metszési kört kell adniok az ernyőn. Jelöljük a lyuk rádiuszát $r$-rel, a fényforrás lencsétől mért távolságát $t$-vel; ekkor képének távolsága a lencsétől: $tf\left(t-f\right)$. Hasonló háromszögekből: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \frac{h}{r}=\frac{A}{t}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \frac{h}{2r}=\frac{t+\frac{tf}{t-f}-A}{\frac{tf}{t-f}}\mathrm{.}}\hfill \end{array}}$ Ebből $h/r$ kiejtése és rendezés után ez az egyenlet következik $t$-re nézve: $\begin{array}{c}{\displaystyle 2t^2-2At+Af=0.}\end{array}$ Ennek megoldása: $\begin{array}{c}{\displaystyle t=\frac{A}{2}\pm \frac{1}{2}\sqrt[]{A\left(A-2f\right)}\mathrm{.}}\end{array}$ A mi esetünkben a fényforrás megkívánt elhelyezésére ez a két eredmény következik: $t_1=6\text{cm}$, $t_2=3\text{cm}$. Az első esetben a lencsét a fényforrástól 6 cm-re kell elhelyeznünk. Érdekes, hogy a második megoldás is eleget tesz a feladat követelményének, bár virtuális képalkotással jár (10. ábra). 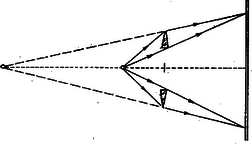    10. ábra   Triviális megoldás még $t=0$. A feladat csak akkor realizálható, ha $A>2f$.   4. A 11. ábra szerint összekapcsoltunk $2$ mikrofarados kondenzátort, rézszulfát oldattal megtöltött elektrolizáló edényt és $3$ mikrofarados kondenzátort. Mennyi vörösréz válik le, ha a drótok végeire $100$ voltos áramforrást kapcsolunk ? A vörösréz elektrokémiai egyenértéke $0\mathrm{,}33\text{mg/coulomb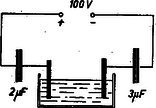}$.     11. ábra   Megoldás. A kondenzátorok eredő kapacitása $2\cdot 3/\left(2+3\right)=1\mathrm{,}2\mu F$. A kondenzátorokat megtöltő töltés $1\mathrm{,}2\cdot {10}^{-6}\cdot 100=1\mathrm{,}2\cdot {10}^{-4}$ coulomb. Ennyi töltés megy be a kondenzátorok szélső lemezeibe és ennyi osztódik meg a belső lemezekből álló fémtestben. Közben ez a töltés átmegy a rézszulfát oldaton és kiválaszt $0\mathrm{,}33\cdot {10}^{-3}\cdot 1\mathrm{,}2\cdot {10}^{-4}=3\mathrm{,}96\cdot {10}^{-8}$ gramm vörösrezet.   Az 1969. évi fizikai tanulmányt verseny eredménye:     I. díj: Maróti Péter (Szeged, Ságvári E. g. IV. o. t. Tanára: Vozáry Pálné).  II. díj: Spitzer József (Budapest, Vörösmarty M. g. IV. o. t. Tanára: Óhegyi Ernő). III. díj: Somorjai gábor (Budapest, I. István g. III. o. t. Tanára: Főzy István).   A további helyezettek: 4. Erdős Géza (Budapest, József A. g. IV. o. t.), 5. Horváthy Péter (Budapest, Fazekas M. g. III. o. t.), 6. Háy György (Budapest, Eötvös J. g. IV. o. t.), 7. Horváth András (Budapest, Ady E. g. IV. o. t.), 8. Ormos Pál (Szeged, Radnóti M. g. III. o. t.), 9. Grandpierre Attila (Budapest, Fazekas M. g. IV. o. t.), 10. Harmat Péter (Mosonmagyaróvár, Kossuth L. g. III. o. t.). ${}^{*}$*${\alpha }_k$ értékét differenciálszámítással, vagy a következő összefüggés felhasználásával kaphatjuk meg: $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{1+A\text{cos}\alpha }=\sqrt[]{\frac{1}{1-A^2}\left[1-{\left(\frac{A+\text{cos}\alpha }{1+A\text{cos}\alpha }\right)}^2\right]}\mathrm{.}}\end{array}$  (Bodó Zalán)