Kezdőlap


Cím:	1968. évi Eötvös Loránd Fizikaverseny
Füzet:	1969/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1968. október 19-én rendezte fizikai versenyét. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

m

tömegű,

L

hosszúságú rúd egyik végén ékkel van alátámasztva, másik végén fonállal van felfüggesztve. A fonalat elégetjük. A mozgás megindulásának pillanatában mekkora erővel nyomja a rúd az éket?

Megoldás: A rúd mozgását

β

szöggyorsulással kezdi el.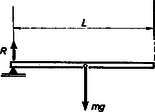

1. ábra

Ha az éket tekintjük tengelynek (

1

. ábra), akkor a súly forgatónyomatéka

m g L / 2

és a tehetetlenségi nyomaték a rúd végpontjára vonatkoztatva

m L^{2} / 3

. Ezek hányadosa adja a szöggyorsulást:

\begin{matrix} β = \frac{m g L / 2}{m L^{2} / 3} = \frac{3 g}{2 L} . \end{matrix}

Az éknél

R

reakcióerő nyom felfelé. A

β

szöggyorsulást úgy is számíthatjuk, mintha a rúd a középpontja körül forogna; ekkor a forgatónyomaték

R L / 2

, a tehetetlenségi nyomaték

m L^{2} / 12

és ismét ezek hányadosa adja a szöggyorsulást:

\begin{matrix} β = \frac{R L / 2}{m L^{2} / 12} = \frac{6 R}{m L} . \end{matrix}

A szöggyorsulás kétféleképp kiszámított értékeit egyenlővé téve:

\begin{matrix} \frac{3 g}{2 L} = \frac{6 R}{m L} . \end{matrix}

Innen az éknél működő erő:

\begin{matrix} R = \frac{m g}{4} . \end{matrix}

Tehát a mozgás megindulásának pillanatában a rúd súlyának negyedével nyomja az éket. A szöggyorsulás

3 g / 2 L

értékéből megtudjuk, hogy a rúd súlypontja

β L / 2 = 3 g / 4

, vége pedig

β L = 3 g / 2

gyorsulással indul el.

4

méter mély medence fenekén síktükör fekszik. Egy fényképész gépével

2

méter magasan van a víz szintje felett. A víz szintje alatt

2

méter mélyen hal úszik. Hány méterre kell a gép lencséjét élesre állítani, ha a) az úszó halat, b) a hal tükörképét akarja lefényképezni?

Megoldás. A víz alól

β

mélységből induló fénysugár (

2

. ábra) a vízben

β

szöget alkot a beesési merőlegessel.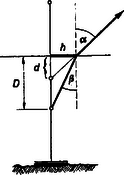

2. ábra

A levegőbe kilépve a fénysugár a beesési merőlegestől törik, vele

α

szöget alkotva, azután a levegőben úgy halad tovább, mintha

d

mélységből jönne. Ha

n

a törésmutató, akkor a fénytörés törvénye szerint:

\begin{matrix} n = \frac{sin α}{sin β} . \end{matrix}

Kis szögeknél a sinus helyett vehető a tangens és ekkor közelítő pontossággal:

\begin{matrix} n = \frac{tg α}{tg β} = \frac{h / d}{h / D} = \frac{D}{d}, vagyis d = \frac{D}{n} . \end{matrix}

Tehát

n

törésmutatójú anyagréteg a törésmutató arányában hozza közelebb a tárgyat. De ez csak kis szögeknél érvényes, ha majdnem pontosan merőlegesen vagyunk a hal fölött. Szigorúan véve nincs is képalkotás, az egyetlen

D

mélységben levő pontból kiinduló fénysugarak a levegőben úgy haladnak tovább, hogy hátrafelé rajzolt meghosszabbításaik nem találkoznak egyetlen pontban. A gyakorlatban ez a körülmény nem szokott szerepet játszani, mert csak szűk sugárnyalábot használunk fel. A víz törésmutatója

4 / 3

.
a) esetben a levegőben mért

2

méterhez még

2 : 4 / 3 = 1, 5

métert kell hozzáadnunk és a szükséges élesre állítási távolság

2 + 1, 5 = 3, 5

méter.
b) esetben figyelembe kell vennünk, hogy a hal tükörképe olyan sajátságú, mintha a vízben még

2

méterrel volna a fenék alatt. Tehát a sugármenet olyan, mintha

6

méteres vízben megtett út után kerülne ki a levegőbe. Tehát a levegőben számított

2

méterhez

6 : 4 / 3 = 4, 5

métert kell hozzáadni és így a szükséges élesre állítási távolság

2 + 4, 5 = 6, 5

méter.

3. A rajz szerinti kapcsolásban (3. ábra) mindkét ohmos ellenállás egyenlő (R). Az

A

és

B

pontokra váltófeszültséget kapcsolunk. Mekkora legyen

L

és

C

, hogy az egész berendezés

R

nagyságú ohmos ellenállásként viselkedjék?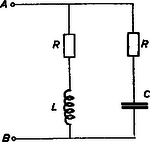

3. ábra

Megoldás. Mindkét ágban

ω

körfrekvenciájú sinusos váltóáram folyik:

\begin{matrix} I_{L} & = \frac{U_{0}}{\sqrt[]{R^{2} + ω^{2} L^{2}}} \cdot sin (ω t - φ_{L}), \\ I_{C} & = \frac{U_{0}}{\sqrt[]{R^{2} + 1 / ω^{2} C^{2}}} \cdot sin (ω t + φ_{C}) . \end{matrix}

φ_{L}

, illetve

φ_{C}

az áramerősség fáziskülönbsége a feszültséghez képest. A váltóáramok tanából ismeretes, hogy:

\begin{matrix} tg φ_{L} & = \frac{ω L}{R}, \\ tg φ_{C} & = \frac{1 / ω C}{R} . \end{matrix}

A szögfüggvények összefüggései alapján a sinus és cosinus:

\begin{matrix} sin φ_{L} = \frac{ω L}{\sqrt[]{R^{2} + ω^{2} L^{2}}}, cos φ_{L} = \frac{R}{\sqrt[]{R^{2} + ω^{2} L^{2}}}, \\ sin φ_{C} = \frac{1 / ω C}{\sqrt[]{R^{2} + 1 / ω^{2} C^{2}}}, cos φ_{C} = \frac{R}{\sqrt[]{R^{2} + 1 / ω^{2} C^{2}}} . \end{matrix}

A két sinusos áram összege a teljes áram, amelynek

U_{0} sin ω t / R

-nek kell lennie.
Ismeretes, hogy ugyanazon frekvenciájú, de különböző fázisú sinus-függvények formálisan a paralelogrammatétel szerint adhatók össze. (Lásd például a Középiskolai Matematikai Lapok 1964. évi februári számának 82. oldalán.) Az amplitúdókat a fázisszögek felhasználásával arányos hosszúságú nyilakkal rajzoljuk fel és ezeket a paralelogramma-szerkesztéssel összegezzük. Az átló megadja az eredő sinus-függvény amplitúdóját és fázisszögét.
A mi esetünkben mérjük fel a két váltóáram amplitúdóját és fázisszögét az adott váltófeszültséghez képest (4. ábra).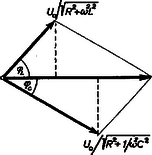

4. ábra

A paralelogramma átlójának a feladat szerint a váltófeszültség irányába kell esnie. Eszerint az átlóra merőleges vetületeknek ellentétesen egyenlőknek kell lenni:

\begin{matrix} \frac{U_{0}}{\sqrt[]{R^{2} + ω^{2} L^{2}}} \cdot sin φ_{L} = \frac{U_{0}}{\sqrt[]{R^{2} + 1 / ω^{2} C^{2}}} \cdot sin φ_{C}; \end{matrix}

Felhasználva a fázisszögek sinusainak előbb felírt értékeit:

\begin{matrix} \frac{ω L}{R^{2} + ω^{2} L^{2}} = \frac{1 / ω C}{R^{2} + 1 / ω^{2} C^{2}} . \end{matrix}

Ennek rendezésével kapjuk:

\begin{matrix} R^{2} = \frac{L}{C} \cdot \frac{1 - ω^{2} L C}{1 - ω^{2} L C} . \end{matrix}

Tehát annak feltétele, hogy az eredő áramerősség a rákapcsolt feszültséggel egyező fázisban legyen:

\begin{matrix} R^{2} = \frac{L}{C} . \end{matrix}

Ha ez a feltétel teljesül, akkor az egész berendezés ohmos ellenállásként viselkedik. De vajon mekkora ohmos ellenállásként?
Minden, a 3. ábra szerinti párhuzamos kapcsolásnál a fázisok tangenseinek szorzata: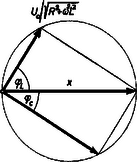

\begin{matrix} tg φ_{L} \cdot tg φ_{C} = \frac{ω L}{R} \cdot \frac{1 / ω C}{R} = \frac{L}{C R^{2}}, \end{matrix}

függetlenül a frekvenciától. De a mi esetünkben, ha megvalósítjuk az

R^{2} = L / C

feltételt:

\begin{matrix} tg φ_{L} \cdot tg φ_{C} = 1, \end{matrix}

vagyis a fázisszögek pótszögek,

φ_{L} + φ_{C} = 90^{\circ}

, a 4. ábra paralelogrammája téglalap és annak átlója egy Thales-kör átmérője.

5. ábra

Az 5. ábrában téglalapként rajzolt paralelogramma átlója, mint egy derékszögű háromszög átfogója:

\begin{matrix} x = \frac{U_{0}}{\sqrt[]{R^{2} + ω^{2} L^{2}}} : cos φ_{L} = \frac{U_{0}}{R} . \end{matrix}

Felhasználtuk

cos φ_{L}

előbb felírt értékét. Tehát betartva a feszültség fázisát teljesítő

R^{2} = L / C

feltételt egyidejűleg teljesül az a kívánság is, hogy az eredő ellenállás

R

. Vagyis a feladat megoldása: úgy választandó

L

és

C

, hogy hányadosuk

R

ellenállás négyzete legyen. Ez a feltétel független a frekvenciától. A rezonancia esete sem kivétel, ekkor a téglalapból négyzet lesz.

A verseny eredménye. Az I. díjat nyerte Babai László, a budapesti tudományegyetem matematikus hallgatója, (tavaly a budapesti Fazekas gimnáziumban Hutai Ferenc tanítványa). A két II. díjat nyerték: Marossy Ferenc honvéd (tavaly a budapesti Fazekas gimnáziumban Hutai Ferenc tanítványa) és Nagy Zsigmond, a budapesti tudományegyetem matematikus hallgatója, (tavaly a budapesti Kaffka M. gimnáziumban Fekete Eszter tanítványa). III. díjat kapott Vetier András, a budapesti tudományegyetem matematikus hallgatója, (tavaly a budapesti Fazekas gimnáziumban Hutai Ferenc tanítványa). A versenyen résztvevő középiskolai tanulók közül dicséretet és könyvjutalmat kapott Maróti Péter, a szegedi Ságvári gimnázium IV. o. tanulója (tanára Dr. Vozáry Pálné). Dicséretet kaptak még a gimnáziumi tanulók közül: Andor László, Bajmóczy Ervin, Balogh Gábor, Horváthy Péter, az érettségizettek közül Bernus Péter, Egri Róbert, Grósz Tamás, Várhelyi Ferenc.