Kezdőlap


Cím:	Testek gördülése, a haladó és forgómozgás együttes fellépése III. Energetikai jellemzés
Szerző(k):	Nagy László
Füzet:	1969/január, 33. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A csúszásmentes gördülés energiaviszonyai

Az előzőekben (1. az I. és a II. részt a májusi, ill. szeptemberi számban) említettük, hogy csúszásmentes gördülés során a pillanatnyi forgástengely a gördülő hengernek a felülettel való érintkező egyenese, illetve gömb esetén a pillanatnyi forgástengely az érintkezési ponton megy keresztül. A gördülő test pontjainak sebessége általában más és más (1. ábra), ezért a mozgási energiának

W_{kin} = \frac{1}{2} \sum m_{1} \cdot v_{i}^{2}

összefüggés alapján történő kiszámítása matematikai nehézségekbe ütközik.

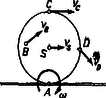1. ábra

Mivel a gördülés úgy tekinthető, mint a pillanatnyi forgástengelyek körül történő elemi forgások sorozata, azért a gördülő test mozgási energiája a pillanatnyi forgástengelyre vett forgási energia lesz:

\begin{matrix} W_{kin} = \frac{1}{2} \cdot Θ_{A} ω^{2} . \end{matrix}

Steiner tétele értelmében

Θ_{A} = Θ_{s} + m r^{2}

, ezért

W_{kin} = (1 / 2) Θ_{s} ω^{2} + (1 / 2) m \cdot r^{2} \cdot ω^{2} = (1 / 2) Θ_{s} ω^{2} + (1 / 2) m \cdot v_{s}^{2}

, ahol felhasználtuk a csúszásmentes gördülést kifejező

v_{s} = ω \cdot r

kinematikai kapcsolatot.
Ezek szerint a gördülő test összes kinetikus energiája a súlypont haladó mozgásából származó energiának és a súlyponton átmenő tengely körüli forgómozgásból származó energiának az összege.

Az energiatétel és az energiamegmaradás elvének alkalmazása

A dinamikai tárgyalással egyenértékűen alkalmazhatjuk az energiatételt. Nézzük meg ezt egy előzőekben tárgyalt problémán (2. ábra).

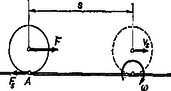2. ábra

Számítsuk ki, mekkora sebességre tesz szert a test

s

út befutása után, ha a súlypontján átmenő állandó nagyságú erő hatására csúszásmentesen gördül.
A végzett munkát és a kinetikai energia növekedését egyenlővé téve

\begin{matrix} F \cdot s = (1 / 2) Θ_{s} ω^{2} + (1 / 2) m v_{s}^{2}, \end{matrix}

majd felhasználva az

ω = v_{s} / r

összefüggést,

v_{s}

számítható. Hogy a végzett munkában sem

F_{n}

, sem

m g

munkája nem szerepel, az nyilvánvaló. Mindkét erő merőleges az elmozdulásra, ezért munkavégzésük 0. De miért nem szerepel

F_{s}

munkája? Mint említés történt,

F_{s}

vagy a nyugalmi vagy határesetben a tapadási súrlódás.
Az erő a pillanatnyi forgástengelyen megy keresztül, de ezeknek a pontoknak a pillanatnyi sebessége zéró. Az elemi elmozdulásoknak nincs erőirányú vetülete, ezért a végzett elemi munka is zérus. Így általában is igaz, hogy nyugalomban levő felület esetén a nyugalmi és tapadási súrlódás munkája 0.
Ugyanazt az eredményt kapjuk, ha a munkavégzés

W = M \cdot α

képlete alapján a pillanatnyi forgástengelyre képezzük a

\sum M Δ α = \sum M ω Δ t

összeget, ahol

M =

= F \cdot r

\sum ω Δ t = α

r \sum ω Δ t = s

. Az

s

a súlypont által megtett út. A végzett munkából jelenleg is kimarad

F_{s}

(természetesen

m g

és

F_{n}

is), mert átmegy a pillanatnyi forgástengelyen és így e tengelyre a nyomatéka 0.
A leggyakrabban a mechanikai energiák megmaradásának elve alkalmazható, melynek feltétele, hogy a testre ható erők munkája 0 legyen. Ezen erők közé nem szabad a gravitációs erőt besorolni, mert annak munkája a helyzeti energia megváltozásának figyelembe vételével számítandó.
A 3. ábra a lejtőn legördülő test esetét mutatja, melynél a 2. ábrával kapcsolatban mondottak értelmében

F_{s}

és

F_{n}

munkája 0.

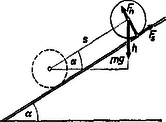3. ábra

Igaz tehát az, hogy

\begin{matrix} (1 / 2) m v_{s}^{2} + (1 / 2) Θ_{s} ω^{2} = m \cdot g \cdot h . \end{matrix}

ω = v_{s} / r

figyelembe vételével például

v_{s}

h

függvényében számítható.

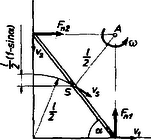4. ábra

Az ismételten visszatérő 4. ábra szerinti elrendezésben (fal mellett súrlódásmentesen lecsúszó rúd)

F_{n 1}

és

F_{n 2}

munkája 0, mert az egyik szemlélet szerint mindkettő átmegy a pillanatnyi forgástengelyen, vagy a másik szemlélet szerint, mert mindkettő merőleges támadáspontjának pillanatnyi elmozdulására (sebességére). Ezért

\begin{matrix} m \cdot g \frac{l}{2} (1 - sin α) = \frac{1}{2} (\frac{1}{12} m l^{2} + m \frac{l^{2}}{4}) ω^{2} . \end{matrix}

Ebből az összefüggésből

ω

, majd

v_{s}

, számítható:

\begin{matrix} ω = \sqrt[]{\frac{3 g \cdot (1 - sin α)}{l}}, és \\ v_{s} = ω \frac{l}{2} = \sqrt[]{\frac{3 g \cdot l \cdot (1 - sin α)}{4}} \end{matrix}

Egy másik probléma, melyet az előző részben nem vizsgáltunk meg, az egyik végén csapágyazott és vízszintes helyzetben elengedett rúd esete (5. ábra).

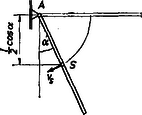5. ábra

Itt az

F_{A}

erő munkája 0, mert egyrészt az

A

pont nem mozdul el, vagy a másik szemlélet szerint azért, mert

F_{A}

átmegy a forgástengelyen. Ezért

\begin{matrix} m \cdot g \cdot (l / 2) \cdot cos α = (1 / 2) (1 / 3) m \cdot l^{2} \cdot ω^{2}, \end{matrix}

amiből

\begin{matrix} ω = \sqrt[]{\frac{3 g \cdot cos α}{l}} és v_{s} = ω l / 2 = \sqrt[]{\frac{3 g \cdot l \cdot cos α}{4}} . \end{matrix}

v_{s}

ismeretében pedig már számolható a tengelyben ébredő centripetális erő, ezzel az előzőekben ismertetett dinamikai elemzés teljessé tehető.
A két utóbbi esetben hangsúlyoznunk kell, hogy a sebességeket nem az idő, hanem a hely függvényében tudjuk elemi módszerekkel meghatározni. Lényegesen bonyolultabb a helyzet csúszó gördülés esetén, amikor a súrlódási együttható, s ezzel a súrlódási erő nagysága is adott. Ekkor a súrlódási erő munkája nem 0, tehát az energiatételben is szerepelni fog. A 6. ábrán látható elrendezésben meg kell határozni, hogy mennyit csúszik a test a felületen, míg a súlypont

s

utat tesz meg.

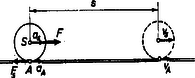6. ábra

A súlypont gyorsulása

a_{s} = F / m - μ g

, a szöggyorsulás

β = \frac{μ \cdot m \cdot g \cdot r}{Θ_{s}}

, ezzel az

A

pont gyorsulása^{$^{*}$}

\begin{matrix} a_{A} = a_{s} - β \cdot r = \frac{F}{m} - μ \cdot g - \frac{μ \cdot g \cdot m \cdot r^{2}}{Θ_{s}} . \end{matrix}

s

út megtételéhez szükséges idő

\begin{matrix} t = \sqrt[]{\frac{2 s}{a_{s}}}, \end{matrix}

és a két felület relatív sebességéből származó út

\begin{matrix} s_{1} = \frac{a_{A}}{2} t^{2} . \end{matrix}

A súrlódás folytán végzett munka*

\begin{matrix} W = F_{s} \cdot s_{1} = μ \cdot m \cdot g \cdot s [1 - \frac{m^{2} \cdot r^{2} \cdot μ \cdot g}{Θ_{s} (F - μ \cdot m \cdot g)}] . \end{matrix}

Az energiatétel értelmében

\begin{matrix} F \cdot s - μ \cdot m g \cdot s [1 - \frac{m^{2} \cdot r^{2} \cdot μ \cdot g}{Θ_{s} (F - μ \cdot m \cdot g)}] = \frac{1}{2} m \cdot v_{s}^{2} + \frac{1}{2} Θ_{s} ω^{2} . \end{matrix}

Csakhogy most

v_{s} \neq r \cdot ω

, hanem*

v_{s} = a_{s} \cdot t = \sqrt[]{2 s (\frac{F}{m} - μ g)}

, továbbá

ω = β \cdot t =

\begin{matrix} = \frac{μ \cdot m g \cdot r}{Θ_{s}} \sqrt[]{\frac{2 s m}{F - μ \cdot m g}} . \end{matrix}

Az energiatétel és e két utolsó egyenlet egyikének felhasználásával vagy

v_{s}

vagy

ω

számítható*, mindkét összefüggésnek az energiatételbe való helyettesítése természetesen azonosságot ad.*
E számításokból is látható, hogy csúszó gördülés esetén nem érdemes az energiatételt alkalmazni, kinematikai és dinamikai elemzésből a probléma megoldása kényelmesebben adódik. A probléma teljesen hasonló megoldásokat igényel akkor, ha a súlypont kezdősebessége vagy a kezdeti szögsebesség nem 0, illetve ezeknek egyik speciális eseteként

F = 0

. Ilyen feladat szerepelt az 1966. évi tanulmányi verseny 2. fordulójában, ahol szintén nem volt célszerű energetikai vizsgálatot végezni.

^{$^{*}$}A csillaggal megjelölt részek számolását az olvasónak célszerű elvégeznie.