Cím: 1968. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1969/november, 97 - 102. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Bebizonyítandó, hogy nincs olyan, természetes számokból álló végtelen sorozat, amelynek nem minden eleme egyenlő, s amelynek minden eleme (a másodiktól kezdve) a két szomszédos elem harmonikus közepe. (a és b harmonikus közepe 2aba+b.)

 
Megoldás. Abból az észrevételből indulunk ki, hogy ha h az a, b számok harmonikus közepe, akkor 1h az 1a,1b számok számtani közepe, hiszen a h=2aba+b értékre 1h=12(1a+1b). A feladat állítása eszerint a következő módon fogalmazható át: Bebizonyítandó, hogy a természetes számok reciprokaiból nem alkotható olyan végtelen sorozat, amelyben nem minden elem egyenlő, s amelyben minden elem (a másodiktól kezdve) a két szomszédos elem számtani közepe.
Ez a kijelentés más szóval azt mondja ki, hogy a természetes számok reciprokaiból nem alkotható nem csupa egyenlő számból álló végtelen számtani sorozat. Ennek helyessége nyomban következik abból, hogy a természetes számok reciprokai mindannyian a [0,1] intervallumban helyezkednek el, viszont egy nem csupa egyenlő számból álló végtelen számtani sorozat elemeinek abszolút értéke minden határon túl nő.
 
Megjegyzés. 1. Lényeges a feladatnak az a megszorítása, hogy a végtelen sorozat nem minden eleme egyenlő, mert különben pl. 1, 1, 1,... ellenpéldát adna a feladat állítására.
2. A feladat állítása akkor is igaz, ha nem természetes, hanem egész számokról szól. Ennek helyessége fenti megoldásunkból nyomban adódik, ha benne a [0,1] intervallum helyett a [-1,1] intervallumról szólunk.
3. Nem igaz a feladat állítása, ha benne racionális számok végtelen sorozatáról vagy természetes számok véges (tetszőlegesen előírt hosszúságú) sorozatáról van szó. Az első módosítást az 1, 12, 13,...,1n,... sorozat példája cáfolja, a másodikat pedig a véges
n!,n!2,n!3,...,n!n
sorozat, amelynek minden eleme természetes szám.
 
Második feladat. Adott a síkban egy egyenes, egy ncm sugarú kör (n egész szám) és a körben 4n darab 1cm-es szakasz. Bizonyítsuk be, hogy húzható az adott egyenessel párhuzamosan vagy rá merőlegesen olyan húr, amelynek legalább két szakasszal van közös pontja.
 
Megoldás. Vetítsük a 4n szakasz mindegyikét az adott egyenesre (ezt vízszintesnek mondjuk) és egy rá merőleges (függőlegesnek mondott) egyenesre. A vízszintes vetületek hossza legyen a1, a2,...,a4n, a függőlegeseké pedig b1, b2,...,b4n. A feladat állítása egyértelmű azzal a kijelentéssel, hogy vagy a vízszintes, vagy a függőleges vetületek között van kettő, amelyeknek van közös pontjuk.
Az i-edik szakasz olyan (esetleg szakasszá elfajuló) derékszögű háromszög átfogója, amelynek vízszintes befogója ai, függőleges befogója pedig bi hosszúságú (1. ábra).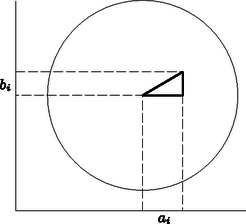
 
 

1. ábra
 

Minthogy a háromszög két oldalának összege a harmadiknál nagyobb,
ai+bi≥1.
Itt az egyenlőséget is meg kellett engednünk, mert számolunk azzal, hogy a vetített szakasz vízszintes vagy függőleges. Eredményünkből következik, hogy mind a 4n szakasz vetületeinek összege
∑ai+∑bi≥4n.
Itt és a következőkben is minden összegezés az i=1,2,...,4n értékekre terjed ki.
Ha a vízszintes vetületek között nincs két közös pontú, akkor ezek együttesen nem fedik le az n-sugarú kör 2n hosszúságú vízszintes vetületét, tehát
∑ai<2n.
Ugyanígy, ha a függőleges vetületek között nincs két közös pontú, akkor
∑bi<2n.
Ha tehát egyik eset sem következik be, akkor
∑ai+∑bi<4n.
Ez ellentmond fenti eredményünknek. Kell tehát, hogy a mondott két eset valamelyike bekövetkezzék, ami ‐ mint megállapítottuk ‐ a feladat állításának helyességét mondja ki.
 
Megjegyzés. A feladat megoldásakor zárt szakaszokra gondoltunk, azaz a szakaszokhoz végpontjaikat is hozzászámítottuk. Igaz azonban a feladat állítása nyílt, tehát végpontjaiktól megfosztott szakaszokra is, ennek bizonyításához azonban ki kell egészítenünk megoldásunkat.
Ha nyílt szakaszokkal dolgozunk, akkor a kör 2n hosszúságú vetületén elhelyezkedő, közös pont nélküli vetületi szakaszok hosszának összege 2n is lehet, hiszen most a végpontjukkal érintkező szakaszoknak nincs közös pontja. Így tehát csak ∑ai≤2n, ∑bi≤2n és ezekből a
∑ai+∑bi≤4n
eredményhez juthatunk, ami nem jelent ellentmondást.
Ha azonban így nem jutunk ellentmondáshoz, tehát a feladat állításának bizonyításához sem, akkor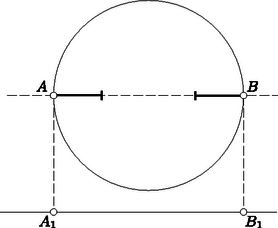
∑ai+∑bi=4n,
tehát ∑ai=2n. Ez azt jelenti, hogy a vízszintes vetületek (végpontjaikkal együtt) a kör teljes vízszintes vetületét, az A1B1 szakaszt beborítják (2. ábra).
 
 

2. ábra
 

Ekkor a vetületek között van A1 kezdőpontú és B1 végpontú is. Ilyen vetületet azonban csak a kör vízszintes AB átmérőjén elhelyezkedő szakaszok adhatnak. Ebben az eddig el nem intézett esetben tehát az adott egyenessel párhuzamos AB egyenes kielégíti a feladat követelményét, hiszen nemcsak közös pontja van két szakasszal, hanem tartalmazza is azokat.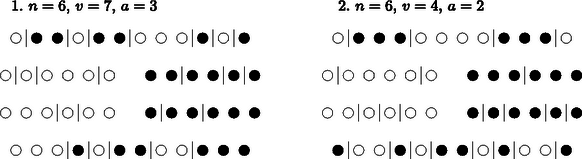
 
Harmadik feladat. Minden lehetséges módon elrendezünk egy sorban n fehér és n fekete golyót. Minden elrendezésben megállapítjuk a színváltások számát. Bizonyítsuk be, hogy ugyanannyi elrendezésben van n-k színváltás, mint ahányban n+k színváltás (0<k<n).
 
I. megoldás. Kiszámítjuk, hogy hány golyóelrendezésben van v színváltás. Két esetet különböztetünk meg aszerint, hogy v páratlan-e, avagy páros.
 
Első eset. Ha v páratlan, legyen v=2a+1. A golyóelrendezés szakaszainak mondjuk a más színű golyók által közrefogott egyszínű golyókat. Minthogy a színváltások száma 2a+1, a szakaszok száma 2a+2, tehát a+1 fehér és ugyanannyi fekete szakasz van. Ha az a+1 fehér szakaszt összetoljuk, az n fehér golyó sorában a szakaszhatár helyezkedik el. Ezek az n golyó sorában található n-1 golyóközből a közt jelölnek ki. A fekete golyókról ugyanígy elmondhatjuk, hogy golyóelrendezésünk az n fekete golyó sorát a+1 szakaszra bontja fel, azaz e sor n-1 golyóköze közül a közt jelöl ki (a 3. ábra 1. részének első két sora szemlélteti a mondottakat egy olyan golyóelrendezésre, amelynél n=6 és v=7, tehát a=3).
 
 

3. ábra
 

Ilyen módon minden vizsgált golyóelrendezés két n-1 elemből alkotott a-ad osztályú kombinációt szolgáltat. Két-két golyóelrendezés azonban ugyanazt a kombinációpárt adja, ti. azok, amelyekben mind a fehér, mind a fekete szakaszok hossza és elrendezése ugyanaz, csak éppen az egyik fehér, a másik pedig fekete szakasszal kezdődik. Akárhogyan választunk is meg egy kombinációpárt, tehát bontjuk a+1 szakaszra a fehér golyók sorát és a fekete golyók sorát is, e szakaszokat váltogatva sorbarakhatjuk és olyan golyóelrendezést kapunk, amelyben v=2a+1 színváltás van. Ezt a sorbarakást kétféleképpen végezhetjük el, mert az elrendezést fehér szakasszal vagy fekete szakasszal kezdhetjük.
Ezek szerint a v színváltású golyóelrendezések száma a mondott két kombináció megválasztási lehetőségei számának kétszerese. Minthogy mindegyik kombináció (n-1a)-féleképpen választható meg, a v színváltású golyóelrendezések száma
2(n-1a)2.

Ha a feladatban szereplő n-k szám páratlan, akkor páratlan n+k is, hiszen a két szám különbsége, 2k páros. Eredményünk tehát mindkét esetben alkalmazható, és v=n+k esetben
2(n-1b)2
az eredmény, ahol n-k=2a+1 mintájára n+k=2b+1 határozza meg b értékét. Ezek szerint a+b=n-1, és a binomiális együtthatók jól ismert (mk)=(mm-k) tulajdonsága szerint
(n-1a)=(n-1b),
ami a fentiek szerint a kapott két eredmény egyenlőségét, tehát páratlan v esetére a feladat állításának helyességét mondja ki.
 
Második eset. Ha v páros, legyen v=2a. Az első esethez hasonlóan járunk el, a golyóelrendezést ismét szakaszokra bontjuk fel, és most 2a+1 szakaszhoz jutunk. Ha az elrendezés fehér szakasszal kezdődött, akkor a+1 fehér és a fekete szakasz van. Egyelőre figyelmen kívül hagyjuk a fekete szakasszal kezdődő elrendezéseket, amelyekről a színeket felcserélve hasonlót mondhatunk el. Ha az a+1 fehér és a fekete szakaszt összetoljuk, az n fehér golyó sorának n-1 köze közül a helyen, a fekete golyók sorának n-1 köze közül pedig a-1 helyen van szakaszhatár (a mondottakat a 3. ábra 2. részének első két sora szemlélteti egy olyan golyóelrendezésre, amelynél n=6 és v=4, tehát a=2).
Az első eset mintájára elmondhatjuk most, hogy annyi v színváltású golyóelrendezés van, ahányféleképpen két n-1 elemű halmaz egyikéből a elemet, másikából pedig a-1 elemet kiválaszthatunk, megengedve, hogy a két halmaz szerepet cseréljen. Itt a golyóelrendezések és a kombinációpárok egymáshoz rendelése kölcsönösen egyértelmű, az első szakasz színének megválasztása nem okoz kétféleséget, mert ha pl. 1-gyel több a fehér, mint a fekete szakasz, akkor a sorbarakásukat fehér szakasszal kell elkezdenünk. A v színváltású golyóelrendezések száma tehát
2(n-1a)(n-1a-1),
ahol a 2-es szorzó az említett szerepcsere miatt lép fel.
Ha a feladatbeli n-k=2a, akkor n+k is páros: n+k=2b. Az n+k színváltású elrendezések száma tehát
2(n-1b)(n-1b-1).
Minthogy most a+b=n, a binomiális együtthatók már említett tulajdonsága szerint
(n-1a)=(n-1b-1),(n-1a-1)=(n-1b),
a kapott két számosság tehát páros v esetében is egyenlő.
 
II. megoldás. A feladat két halmaz számosságának egyenlőségét mondja ki. Első megoldásunkban megszámláltuk mind a két halmazt és konstatáltuk a két eredmény egyenlőségét. Most megszámlálás nélkül bizonyítjuk a két számosság egyenlőségét oly módon, hogy a két halmaz elemei között kölcsönös egyértelmű hozzárendelést létesítünk. Ilyen hozzárendelés természetesen csak akkor létesíthető, ha mindkét halmazban ugyanannyi elem van.
Eljárásunk ennyiben eltér az első megoldásétól, viszont lényegében mégis azzal azonos, mert annak alapja a kombinációs együtthatók (mk)=(mm-k) tulajdonsága volt, s ennek alkalmazása helyett dolgozhatunk a kombinációknak azzal az egymáshoz rendelésével, amely az említett tulajdonságot szolgáltatja, ha ti. az m elemből kiválasztott k-adosztályú kombinációhoz hozzárendeljük az imént ki nem választott m-k elemből álló kombinációt. Ezzel második megoldásunkat lényegében már elő is adtuk, csak egyes részletek tisztázására van még szükség.
Egy v színváltásos golyóelrendezés az első megoldás előírása szerint az egyszínű szakaszok összetolása révén az n fehér golyóból és az n fekete golyóból álló golyósor szakaszokra bontását határozza meg. Új szakaszokra bontáshoz jutunk, ha ott helyezünk el szakaszhatárokat, ahol az imént nem volt szakaszhatár. Az így kapott szakaszokat váltakozó színekkel sorbarakjuk és új golyóelrendezéshez jutunk. Ez a hozzárendelés azonban ‐ mint az első megoldásban is láttuk ‐ nem egyértelmű, ha ugyanannyi fehér és fekete szakasz van. Ez páratlan v esetén következik be, s ekkor az új elrendezés számára is ugyanannyi fehér és fekete szakasz adódik. Ezt a zavaró kétféleséget megszüntethetjük azáltal, hogy páratlan v esetében megállapodunk abban, hogy egy elrendezésből származtatott új elrendezés pl. ugyanolyan színű szakasszal kezdődjék, mint amilyennel az eredeti kezdődött. (Az új elrendezés származtatását a 3. ábra mutatja be két esetben.)
Az így létesített hozzárendelés minden v színváltású golyóelrendezéshez egy-egy 2n-v színváltásút rendel, mert az n fehér golyó sorában található n-1 köz és az n fekete golyó sorában található n-1 köz, összesen tehát 2n-2 köz közül v-1 helyen volt szakaszhatár, s ezért az új szakaszkijelöléskor (2n-2)-(v-1)=2n-v-1 szakaszhatárt helyeztünk el, így a két n-elemű golyósorban együttesen 2n-v+1 szakaszvég és ugyanennyi szakasz keletkezett, s a váltakozó színekkel történő összerakás valóban 2n-v színváltású elrendezést adott. Ugyanaz az előírás, amely egy v színváltású elrendezésből egy 2n-v színváltáshoz vezetett, egy ilyenből visszavezet az eredeti v színváltásúhoz. Ez biztosítja, hogy valamennyi v=n-k színváltású elrendezés halmaza és valamennyi 2n-v=n+k színváltású elrendezés halmaza között kölcsönös egyértelmű hozzárendelést létesítettünk. A két halmaz tehát egyenlő számosságú.