Kezdőlap


Cím:	Váltóáramú áramkörök számítása
Szerző(k):	Gaál István
Füzet:	1968/november, 165 - 174. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Néhány példa kapcsán módszert mutatunk be arra, hogyan lehet meghatározni a feszültség és az áramerősség pillanatnyi értékét váltóáramú áramkörökben.
Első példaként vizsgáljuk meg a váltakozó feszültségre kötött, sorba kapcsolt önindukcióból ( $L$ ), ellenállásból ( $R$ ) és kapacitásból ( $C$ ) álló lánc áram- és feszültségviszonyait. Jelöljük rendre $i (t)$ -vel, $u_{L} (t)$ -vel és $q (t)$ -vel a $t$ időpontban a körben folyó áramot, az önindukciós tekercsben indukált feszültséget és a kondenzátorban tárolt töltést. KIRCHHOFF II. törvénye szerint bármely időpillanatban az $R$ ellenálláson eső feszültség és a kondenzátor kapcsain uralkodó feszültség algebrai összege egyenlő az $A B$ kapcsokra (1. ábra) kívülről ráadott $U_{0} \cdot sin (ω t)$ hálózati feszültség és az indukciós tekercsben indukált feszültség algebrai összegével:

\begin{matrix} R \cdot i (t) + \frac{q (t)}{C} = u_{L} (t) + U_{0} \cdot sin (ω t) . \end{matrix}

(1)

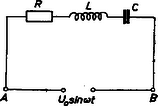1. ábra

Az indukált feszültség a mágneses tér változásának sebességével, a mágneses tér erőssége pedig az árammal arányos. Ez azt jelenti, hogy

u_{L} (t)

az áram változásának sebességével arányos:

\begin{matrix} u_{L} (t) = - L \cdot i' (t) . \end{matrix}

(2)

Egyenletünkben a negatív előjel azt fejezi ki, hogy az indukált feszültség olyan áramot indít a vezetőben, amely az indukáló mágneses teret csökkenti. Az áram-változás sebességét azért jelöltük

i' (t)

-vel, hogy az áram és az áram-változás sebessége közötti szoros kapcsolatot a jelölésmóddal is kiemeljük. A (2)-es egyenletet (1)-be helyettesítve azt kapjuk, hogy:

\begin{matrix} L \cdot i' (t) + R \cdot i (t) + \frac{q (t)}{C} = U_{0} \cdot sin (ω t) . \end{matrix}

(3)

Egyenletünkben három ismeretlen van:

i' (t)

i (t)

és

q (t)

. Ez a három függvény azonban nem független egymástól. Ha például a kondenzátor töltése a

\begin{matrix} q (t) = m \cdot t \end{matrix}

(4)

összefüggés szerint változna, akkor a körben folyó áram (ami nem más, mint

q (t)

változásának sebessége)

\begin{matrix} i (t) = q' (t) = \frac{m t_{1} - m t_{2}}{t_{1} - t_{2}} = m \end{matrix}

(5)

lenne,

i' (t)

pedig azonosan zérus volna. Ha

\begin{matrix} q (t) = \frac{1}{2} \cdot a \cdot t^{2} \end{matrix}

(6)

akkor

\begin{matrix} i (t) = q' (t) = a \cdot t \end{matrix}

(7)

és

\begin{matrix} i' (t) = a . \end{matrix}

(8)

Ugyanis (6) teljesen azonos szerkezetű a szabadesés útképletével:

\begin{matrix} s = \frac{1}{2} \cdot g \cdot t^{2}, \end{matrix}

(9)

és tudjuk, hogy a szabadon eső test mechanikai sebessége (azaz

s

változásának a sebessége)

\begin{matrix} v = s' = g t, \end{matrix}

(10)

gyorsulása pedig (azaz a sebesség változásának sebessége)

\begin{matrix} a = v' = g . \end{matrix}

(11)

Hasonlóképpen, ha

q (t) = Q_{0} sin (ω t - φ)

(12)
akkor

i (t) = q' (t) = Q_{0} ω cos (ω t - φ)

(13)
és

i' (t) = - Q_{0} ω^{2} sin (ω t - φ)

, (14)
miként az a harmonikus rezgőmozgással való analógia alapján nyilvánvaló. Tudjuk ugyanis, hogy az egyensúlyi helyzettől való pillanatnyi kitérés

(x)

, a sebesség és a gyorsulás harmonikus rezgés esetén a következő egyenletekkel írható le:

\begin{matrix} x & = x_{0} sin (ω t), & (15) \\ v & = x' = x_{0} ω cos (ω t), & (16) \\ a & = v' = - x_{0} ω^{2} sin (ω t) . & (17) \end{matrix}

Fizikai érzékünk azt súgja, hogy a (3) egyenletet kielégíti egy

\begin{matrix} q (t) = Q_{0} \cdot sin (ω t - φ) \end{matrix}

(18)

alakú függvény. Sejtésünket behelyettesítéssel igazoljuk.

q (t)

-t és (18)-nak (13) és (14) szerint megfelelő

i (t)

-t és

i' (t)

-t (3)-ba beírva

\begin{matrix} - L Q_{0} ω^{2} sin (ω t - φ) + R Q_{0} ω cos (ω t - φ) + \frac{Q_{0}}{C} sin (ω t - φ) = U_{0} sin (ω t) . \end{matrix}

(19)

Az ismert trigonometrikus összefüggések alapján írható, hogy:

\begin{matrix} - L Q_{0} ω^{2} [sin (ω t) \cdot cos φ - cos (ω t) \cdot sin φ] + R Q_{0} ω [cos (ω t) \cdot cos φ + \\ + sin (ω t) \cdot sin φ] + \frac{Q_{0}}{C} [sin (ω t) \cdot cos φ - cos (ω t) \cdot sin φ] = U_{0} sin (ω t); & (20) \end{matrix}

illetve:

\begin{matrix} sin (ω t) [R Q_{0} ω sin φ + (\frac{Q_{0}}{C} - L Q_{0} ω^{2}) cos φ - U_{0}] + \\ + cos (ω t) [R Q_{0} ω cos φ - (\frac{Q_{0}}{C} - L Q_{0} ω^{2}) sin φ] = 0. & (21) \end{matrix}

Ez az egyenlet akkor teljesül minden

t

időpillanatban, ha mind

cos (ω t)

, mind

sin (ω t)

együtthatója zérus, azaz ha

\begin{matrix} R Q_{0} ω sin φ + (\frac{Q_{0}}{C} - L Q_{0} ω^{2}) cos φ - U_{0} = 0, & (22) \\ R Q_{0} ω cos φ - (\frac{Q_{0}}{C} - L Q_{0} ω^{2}) sin φ = 0. & (23) \end{matrix}

(22) és (23) teljesülése viszont szükséges feltétele is (21) teljesülésének, mert a

t = 0

pillanatban (21) (22)-vel, a

t = \frac{π}{2 ω} = T / 4

időpontban pedig (21) (23)-mal azonos.
(18) próbafüggvény tehát akkor megoldása a (3) egyenletnek, ha a

Q_{0}

és

φ

paraméterek a (22) és (23) egyenlet megoldásai, azaz ha

\begin{matrix} tg φ = - \frac{R}{L ω - \frac{1}{ω C}} \end{matrix}

(24)

és

\begin{matrix} Q_{0} = \frac{U_{0}}{ω \sqrt[]{{(ω L - \frac{1}{ω C})}^{2} + R^{2}}} . \end{matrix}

(25)

(

tg φ

-t (23)-ból fejeztük ki. Utána a már ismert

tg φ

segítségével megállapítottuk

sin φ

és

cos φ

értékét, és ezeket (22)-be helyettesítettük. Így

Q_{0}

kifejezése már csak némi rendezést követelt.)
Ha a (3) egyenlet megoldását ,,ügyetlenül'' megválasztott próbafüggvénnyel kíséreljük meg (pl. próbafüggvénynek a

q (t) = a \cdot t^{2}

-et vagy a

q (t) = Q_{0} \cdot sin (ω t)

függvényt választjuk), akkor a próbafüggvény paramétereinek alkalmas megválasztásával sem tudjuk egyenletünket minden

t

értékre kielégíteni.
A (3) egyenlet általános megoldásáról és a (18) típusú megoldás különleges szerepéről a cikk végén fogunk szólni.
(18), (13), (14), (24) és (25) felhasználásával kiszámíthatjuk a körben folyó áramot, valamint az ellenálláson eső, a kondenzátoron uralkodó és a tekercsben indukált feszültséget. (Jelöljük ezeket a feszültségeket rendre

u_{R} (t)

-vel,

u_{C} (t)

-vel és

u_{L} (t)

-vel.)

\begin{matrix} i (t) = q' (t) = Q_{0} ω cos (ω t - φ) = I_{0} cos (ω t - φ), & (26a) \\ u_{C} (t) = q (t) / C = \frac{Q_{0}}{C} sin (ω t - φ) = \frac{I_{0}}{ω C} sin (ω t - φ), & (26b) \\ u_{R} (t) = R \cdot i (t) = R I_{0} cos (ω t - φ) = R Q_{0} ω cos (ω t - φ), & (26c) \\ u_{L} (t) = - L \cdot i' (t) = + L ω I_{0} sin (ω t - φ) = + L ω^{2} Q_{0} sin (ω t - φ) . & (26d) \end{matrix}

Eredményeink grafikonja a 2. ábrán látható.

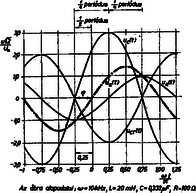2. ábra

Az ábrán feltüntettük a kívülről a láncra adott feszültség

[U_{K} (t)]

menetét is. Az ellenálláson eső feszültség az áramerősséggel szinkronban van, míg a kondenzátoron eső feszültség az áramerősséghez képest negyedperiódust késik. Mivel a (3) egyenlet szorosabb analógiát mutat az egyenáramú áramkörök szokásos egyenleteivel, mint az (1) egyenlet, azért a technikai irodalomban az indukciós tekercs feszültségviszonyait kényelmi szempontból nem az

u_{L} (t) = - L \cdot i' (t)

indukált feszültséggel, hanem az

u_{L T} (t) = - u_{L} (t)

ugyancsak feszültség dimenziójú mennyiséggel szokták jellemezni.

u_{L T}

-t az analógia kedvéért az induktív ,,ellenálláson'' eső feszültségnek szokták nevezni.

u_{L T}

az áramhoz képest negyedperiódust siet.
(3) egyenlet (18) típusú megoldásának paramétereit meghatározó (22) és (23) egyenlethez egyszerű geometriai képet fűzhetünk (3. ábra).

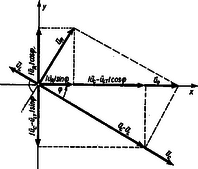3. ábra

Vezessük be a következő négy feszültség amplitúdó vektort:

{\vec{U}}_{L T}

-t,

{\vec{U}}_{R}

-et,

{\vec{U}}_{C}

-t és

{\vec{U}}_{K}

-t úgy, hogy

\begin{matrix} | {\vec{U}}_{L T} | = L ω I_{0} = L ω^{2} Q_{0}, & (26e) \\ | {\vec{U}}_{R} | = R I_{0} = R ω Q_{0}, & (26f) \\ | {\vec{U}}_{C} | = \frac{Q_{0}}{C} = \frac{I_{0}}{ω C}, & (26g) \\ | {\vec{U}}_{K} | = U_{0} & (26h) \end{matrix}

legyen, továbbá

{\vec{U}}_{L T}

és

{\vec{U}}_{C}

legyenek egymással ellentétes irányúak és

{\vec{U}}_{R}

legyen merőleges ezekre a vektorokra és irányát pozitív forgás vigye át

{\vec{U}}_{L T}

irányába. Követeljük meg, hogy

\begin{matrix} {\vec{U}}_{K} = {\vec{U}}_{L T} + {\vec{U}}_{C} + {\vec{U}}_{R} \end{matrix}

(26i)

legyen. A 3. ábra alapján nyilvánvaló, hogy a (22) és a (23) egyenlet éppen a (26i) által előírt vektorösszeadás elvégzését jelenti az

x

és

y

irányú komponensekre való bontás segítségével.
Meg kell jegyeznünk, hogy (26i) nem ekvivalens (3)-mal, mert mint később látni fogjuk, (3)-nak a (26i) által megadottól különböző megoldásai is vannak. (26i) a (18) típusú megoldás paramétereinek meghatározására szolgáló egyenleteket foglalja össze szemléletes alakban. (26i) és (3) között lényeges formai különbség is van. (26i)-ben időben állandó vektorokat adunk össze, míg (3)-ban időtől függő mennyiségek algebrai összegét képezzük.
Második példaként foglalkozzunk a 4. ábrán vázolt áramkörrel.

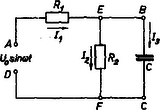4. ábra

KIRCHHOFF I. törvényét az

E

csomópontra alkalmazva

\begin{matrix} i_{1} (t) = i_{2} (t) + i_{3} (t) . \end{matrix}

(27)

KIRCHHOFF II. törvényét az

A E F D

illetve az

E B C F

körökre alkalmazva

\begin{matrix} R_{1} \cdot i_{1} (t) + R_{2} \cdot i_{2} (t) = U_{0} sin (ω t), & (28) \\ R_{2} \cdot i_{2} (t) - \frac{q_{3} (t)}{C} = 0. & (29) \end{matrix}

Keressünk megoldást

\begin{matrix} i_{1} (t) & = I_{10} cos (ω t - φ_{1}), & (30a) \\ i_{2} (t) & = I_{20} cos (ω t - φ_{2}), & (30b) \\ i_{3} (t) & = I_{30} cos (ω t - φ_{3}) & (30c) \end{matrix}

alakban. (12) és (13) alapján látható, hogy a

\begin{matrix} q_{3} (t) = Q_{0} sin (ω t - φ_{3}) \end{matrix}

(31)

választás a

\begin{matrix} q_{3} (t) = Q_{0} ω cos (ω t - φ_{3}) = i_{3} (t) \end{matrix}

(32)

egyenletet akkor elégíti ki, ha

\begin{matrix} I_{30} = Q_{0} ω . \end{matrix}

(33)

(27)-et (28)-ba helyettesítve (30), (31) és (33) felhasználásával, némi trigonometrikus átalakítás után azt kapjuk, hogy

\begin{matrix} [(R_{1} + R_{2}) \cdot I_{20} \cdot cos φ_{2} + R_{1} \cdot I_{30} \cdot cos φ_{3}] cos (ω t) + \\ + [(R_{1} + R_{2}) \cdot I_{20} \cdot sin φ_{2} + R_{1} \cdot I_{30} sin φ_{3} - U_{0}] sin (ω t) = 0, & (34) \\ [R_{2} \cdot I_{20} \cdot cos φ_{2} + \frac{I_{30}}{ω C} sin φ_{3}] cos (ω t) + \\ + [R_{2} \cdot I_{30} \cdot sin φ_{2} - \frac{I_{30}}{ω C} \cdot cos φ_{3}] sin (ω t) = 0. & (35) \end{matrix}

A (21) egyenletnél alkalmazott érvelést megismételve belátható, hogy (34) és (35) teljesülésének az a szükséges és elégséges feltétele, hogy

sin (ω t)

és

cos (ω t)

együtthatói mindkét egyenletben zérussal legyenek egyenlőek. Ezáltal négy egyenletet kapunk a próbafüggvényekben szereplő négy ismeretlen paraméter (

I_{20}

I_{30}

φ_{2}

φ_{3}

) meghatározására. Eredményünk:

\begin{matrix} tg φ_{3} & = \frac{R_{1} R_{2} ω C}{R_{1} + R_{2}} (0 \leq φ_{3} < \frac{π}{2}), & (36a) \\ tg φ_{2} & = - ctg φ_{3} (\frac{π}{2} < φ_{2} \leq π), & (36b) \\ I_{20} & = \frac{U_{0}}{\sqrt[]{{(R_{1} + R_{2})}^{2} + {(R_{1} R_{2} ω C)}^{2}}}, & (36c) \\ I_{30} & = \frac{U_{0} ω C R_{2}}{\sqrt[]{{(R_{1} + R_{2})}^{2} + {(R_{1} R_{2} ω C)}^{2}}} . & (36d) \end{matrix}

I_{10}

és

φ_{1}

meghatározását az olvasóra bízzuk. Állítsuk fel a paraméterek meghatározására szolgáló négy egyenletnek megfelelő két vektor-ábrát is.
Harmadik példaként elemezzük egy

R_{T}

ellenállással terhelt transzformátor feszültség-viszonyait. A primer és szekunder tekercsben folyó váltóáram

[i_{1} (t)

és

i_{2} (t)]

váltakozó mágneses teret kelt a szóban forgó tekercsek belsejében, amely feszültséget indukál a primer, illetve szekunder tekercsben

[u_{1} (t)

és

u_{2} (t)]

. Az ilyen módon indukált feszültség nagyságát a következő képlet adja:

\begin{matrix} u_{1} (t) & = - (L_{11} \cdot i'_{1} (t) + L_{12} \cdot i'_{2} (t)), & (37a) \\ u_{2} (t) & = - (L_{21} \cdot i'_{1} (t) + L_{22} \cdot i'_{2} (t)) . & (37b) \end{matrix}

L_{11}

, ill.

L_{22}

a primer, ill. szekunder tekercs önindukciós együtthatója;

L_{12} = L_{21}

pedig a két tekercs kölcsönös indukciós együtthatója. Ezek az együtthatók légmagos transzformátor esetén csak a tekercsek geometriai jellemzőitől és a menetszámoktól függenek. Ha a primer, ill. szekunder tekercs huzalának OHM törvénye alapján számított ellenállása

R_{1}

, ill.

R_{2}

, akkor KIRCHHOFF II. törvénye szerint:

\begin{matrix} R_{1} \cdot i_{1} (t) = U_{0} sin (ω t) + u_{1} (t), & (38a) \\ R_{2} \cdot i_{2} (t) + R_{T} \cdot i_{2} (t) = u_{2} (t) . & (38b) \end{matrix}

(37) és (38) egyenletek segítségével a korábbiakhoz hasonló meggondolások segítségével a primer és szekunder áram, ill. feszültség kiszámítható. A számítás elvégzését és a vektor-ábra felállítását az olvasóra bízzuk. Vizsgáljuk meg a transzformátor feszültség-viszonyait kapacitással való terhelés esetében is.
Váltóáramú áramköri feladatainkat úgy oldottuk meg, hogy megsejtettük a számunkra lényeges megoldás típusát és egyenleteinkből csak a próbafüggvényben szereplő paraméterek értékeit határoztuk meg. Megemlítjük, hogy ez a módszer teljesen általános, nevezetesen: tetszőleges

L_{ik}

C

és

R

elemekből álló áramköri probléma megoldása megadható elegendően sok

Q_{0} sin (ω t - φ)

típusú függvény ügyes illesztésével, ha a külső feszültség

U_{0} sin (ω t)

lefutású. A paraméterek meghatározására szolgáló egyenletek a vektor-ábrákból is leolvashatóak, ha megismertük azt, hogy az alapegyenleteknek megfelelő vektorábrákat hogyan kell megszerkeszteni. A vektorábrák felrajzolása tulajdonképpen a

sin (ω t - φ)

és

cos (ω t - φ)

függvények szorzatok összegére való bontásának egy geometriailag szemléltetett módja.
Fordítsuk most figyelmünket egy minőségileg más áramköri problémára. Kapcsoljunk első példaképpen

U

egyenfeszültségű áramforrásra

R

ellenálláson keresztül

C

kapacitást. Zárjuk a

K

kapcsolót (5. ábra) a

t = 0

pillanatban rövidre.

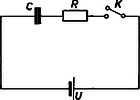5. ábra

Ekkor nyilván minden

t \geq 0

időpontban:

\begin{matrix} R \cdot i (t) + \frac{q (t)}{C} = U \end{matrix}

(39)

és

i (t)

itt is

q (t)

időbeli változásának sebességével egyenlő. Ezt az egyenletet is a

q (t)

függvény alakjának megsejtése útján próbáljuk megoldani.
Előkészítésül szóljunk néhány szót a jól ismert

y = a^{x}

függvényről. (

y = a^{x}

értékét a

10

-es alapú logaritmus táblázat segítségével a következőképpen számítjuk ki. Az egyenlőség mindkét oldalának vegyük a

10

-es alapú logaritmusát:

lg y = x \cdot lg a

. Így

y

-t megkapjuk, ba az

x \cdot lg a

számot a táblázatban visszakeressük.) Vegyük észre, hogy az

y = 10^{x}

függvény számtalan más formában is felírható:

\begin{matrix} y = 10^{x} = 2^{x / lg 2} = 3^{x / lg 3} = ... . \end{matrix}

(40)

(Ugyanis a fenti mennyiségek

10

-es alapú logaritmusa egyenlő.) A matematikában és a fizikában az

y = a^{x}

alakú függvényeket az

\begin{matrix} y = e^{{x/x}_{0}} = exp (\frac{x}{x_{0}}) \end{matrix}

(41)

alakban szokták felírni. Itt

e

egy nevezetes számot jelent, amelynek értéke

2, 71828 ...

és

lg e = 0, 434294 ...

(Ezen adatok birtokában minden

x / x_{0}

értékhez meg lehet határozni az

y = exp (x / x_{0})

értéket a

10

-es alapú logaritmus tábla segítségével.)
Határozzuk meg az

y = exp (- t / τ)

függvény időbeli változásának sebességét. (

τ

rögzített paraméter.) A

t_{1}

és

t_{2}

pontok közötti átlagsebesség:

\begin{matrix} z (t_{1}, t_{2}) = \frac{exp (- t_{2} / τ) - exp (- t_{1} / τ)}{t_{2} - t_{1}} \end{matrix}

(42a)

ill.:

\begin{matrix} z (t_{1}, t_{2}) = exp (- \frac{t_{1} + t_{2}}{2 τ}) \cdot [\frac{exp (- \frac{t_{2} - t_{1}}{2 τ}) - exp (\frac{t_{2} - t_{1}}{2 τ})}{t_{2} - t_{1}}] . \end{matrix}

(42b)

Látható, hogy az átlagsebesség értéke mind

t_{1}

, mind

t_{2}

értékétől függ. Ha az átlagsebesség kiszámítására szolgáló idő-intervallum kicsi, nevezetesen

| \frac{t_{2} - t_{1}}{2 τ} |

egynél lényegesen kisebb, akkor mivel egynél abszolut értékben lényegesen kisebb

x

értékekre (lásd táblázat)

\begin{matrix} exp (x) & \approx 1 + x, ha | x | ≪ 1, & (43a) \\ exp (- x) & \approx 1 - x, ha | x | ≪ 1, & (43b) \end{matrix}

írhatjuk, hogy

| \frac{t_{2} - t_{1}}{2 τ} | ≪ 1

esetén

\begin{matrix} z (t_{1}, t_{2}) \approx exp (- \frac{t_{2} + t_{1}}{2 τ}) \cdot [\frac{(1 - \frac{t_{2} - t_{1}}{2 τ}) - (1 + \frac{t_{2} - t_{1}}{2 τ})}{t_{2} - t_{1}}], \end{matrix}

(44)

és így

\begin{matrix} z (t_{1}, t_{2}) \approx - \frac{1}{τ} \cdot exp (- \frac{t_{2} + t_{1}}{2 τ}), ha | \frac{t_{2} - t_{1}}{2 τ} | ≪ 1. \end{matrix}

(45)

\begin{matrix} x & exp(x) & 1 + x & exp(- x) & 1 - x & relatív hiba \\ 0, 001 & 1, 0010005 & 1, 0010000 & 0, 9990005 & 0, 9990000 & 5 \cdot 10^{- 7} \\ 0, 002 & 1, 0020020 & 1, 0020000 & 0, 9980020 & 0, 9980000 & 5 \cdot 10^{- 6} \\ 0, 005 & 1, 0050125 & 1, 0050000 & 0, 9950125 & 0, 9950000 & 1 \cdot 10^{- 5} \\ 0, 010 & 1, 0100502 & 1, 0100000 & 0, 9900498 & 0, 9900000 & 5 \cdot 10^{- 5} \\ 0, 100 & 1, 1051709 & 1, 1000000 & 0, 9048347 & 0, 9000000 & 5 \cdot 10^{- 3} \end{matrix}

Láthatjuk tehát, hogy elegendően szűk időintervallumra számítva az átlagsebességet az csak a

t = \frac{1}{2} (t_{1} + t_{2})

időértéktől függ és így a (45) egyenlet a

t = \frac{1}{2} (t_{1} + t_{2})

időpillanathoz tartozó pillanatnyi sebességet szolgáltatja. Tehát:

\begin{matrix} y' (t) = - \frac{1}{τ} \cdot exp (- t / τ) . \end{matrix}

(46)

Tegyük fel, hogy a kondenzátoron levő töltés a

\begin{matrix} q (t) = Q_{0} \cdot [1 - exp (- t / τ)] = Q_{0} - Q_{0} exp (- t / τ) \end{matrix}

(47)

összefüggés szerint változik. (Feltesszük tehát, hogy a bekapcsolás pillanatában a kondenzátor nem volt feltöltve.) Felhasználva, hogy az áram a kondenzátoron levő töltés változásának sebességével egyenlő, azt nyerjük, hogy:

\begin{matrix} i (t) = q' (t) = \frac{Q_{0}}{τ} \cdot exp (- t / τ) \end{matrix}

(48)

(48) felírásánál felhasználtuk azt a két egyszerű tényt, hogy

y = z (t) + A

és

x = z (t)

függvények sebessége egyenlő, valamint azt, hogy ha

y = z (t)

és

x = A \cdot z (t)

, akkor

x

sebessége

x' = A \cdot y'

. Itt

A

-val egy tetszőleges állandót jelöltünk. Ezen állítások igazsága az átlagsebesség kiszámítása útján könnyen belátható.
(39)-ből (47) és (48) felhasználásával azt kapjuk, hogy:

\begin{matrix} Q_{0} \cdot \frac{R}{τ} \cdot exp (- t / τ) + \frac{Q_{0}}{C} \cdot [1 - exp (- t / τ)] = U, \end{matrix}

(49)

t ⩾ 0

. Ez az egyenlet akkor teljesül, ha

t ⩾ 0

esetén

\begin{matrix} U = \frac{Q_{0}}{C} \end{matrix}

(50a)

és

\begin{matrix} τ = R \cdot C . \end{matrix}

(50b)

Így a kondenzátoron, illetve az ellenálláson eső feszültség:

\begin{matrix} u_{C} (t) & = U \cdot [1 - exp (- t / τ)], & (51a) \\ u_{R} (t) & = U \cdot exp (- t / τ) . & (51b) \end{matrix}

u_{C} (t)

és

u_{R} (t)

menetét a 6. ábra tünteti fel.

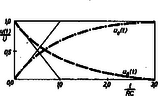6. ábra

Az ábrából a

τ

időállandó jelentése is kitűnik; ez szabja meg a kondenzátor adott mértékű feltöltődéséhez szükséges időt.
Gyakorlásul számítsuk ki, hogy mennyi idő alatt éri el a

100

V egyenfeszültségre kapcsolt

500 Ω

ellenállású és

0, 1

H önindukciójú fojtótekercs a

U / R = 0, 2

A határáramerősség

33

66

és

99 %

-át.

Térjünk vissza most első példánkra: a váltófeszültségre kötött

L R C

láncra. (18), (24), (25) és (26) szerint a

t = 0

pillanatban

\begin{matrix} q (0) & = \frac{U_{0} R}{ω \cdot [{(L ω - \frac{1}{ω C})}^{2} + R^{2}]}, & (52a) \\ i (0) & = \frac{U_{0} \cdot (L ω - \frac{1}{ω C})}{{(L ω - \frac{1}{ω C})}^{2} + R^{2}} . & (52b) \end{matrix}

Ha a láncot a

t = 0

pillanatban kötjük rá a feszültségre, akkor természetesen nem szükségszerű, hogy a kondenzátoron levő töltés éppen az (52a) által megadott érték legyen. Továbbá

i (0)

értéke szükségképpen zérus kell, hogy legyen. Az

L

önindukció miatt ugyanis az áram nem tud a bekapcsolás előtti zérus értékről a bekapcsolás pillanatában valamely zérustól különböző értékre felugrani. Hogyan kell módosítanunk a (18) próbafüggvényt, ha a bekapcsolás jelenségét is le akarjuk írni; ha megköveteljük azt, hogy a próbafüggvény olyan legyen, hogy

i (0) = 0

és

q (0) =

tetszőleges érték a kezdeti (bekapcsolási) feltételeket teljesítse? Az olvasó (3)-ba való behelyettesítéssel meggyőződhetik arról, hogy ha a kondenzátor kezdeti töltése

Q_{K}

, akkor a kondenzátoron levő töltés időbeni változását

{(\frac{R}{2 L})}^{2} > \frac{1}{L C}

esetén a

\begin{matrix} q (t) = Q_{0} sin (ω t - φ) + A exp (- t / τ_{1}) + (Q_{K} + Q_{0} sin φ - A) \cdot exp (- t / τ_{2}) & (53a) \\ 1 / τ_{1} = \frac{R}{2 L} + \sqrt[]{{(\frac{R}{2 L})}^{2} - \frac{1}{L C}}, 1 / τ_{2} = \frac{R}{2 L} - \sqrt[]{{(\frac{R}{2 L})}^{2} - \frac{1}{L C}}; & (53b) \end{matrix}

{(\frac{R}{2 L})}^{2} < \frac{1}{L C}

esetén a

\begin{matrix} q (t) = Q_{0} sin (ω t - φ) - \frac{Q_{K} + Q_{0} sin φ}{sin α} \cdot exp (- t / τ) \cdot sin (Ω t - α), & (53c) \\ \frac{1}{τ} = \frac{R}{2 L}, Ω = \sqrt[]{\frac{1}{L C} - {(\frac{R}{2 L})}^{2}}; & (53d) \end{matrix}

{(\frac{R}{2 L})}^{2} = \frac{1}{L C}

esetén a

\begin{matrix} q (t) = Q_{0} sin (ω t - φ) + (Q_{K} + Q_{0} sin φ + A t) \cdot e^{- t / τ}, & (53f) \\ \frac{1}{τ} = \frac{R}{2 L} & (53g) \end{matrix}

típusú próbafüggvénnyel lehet leírni. Az

α

, ill.

A

paraméter értékét abból a feltételből kell meghatároznunk, hogy

i (0) = 0

. A behelyettesítés, ill. az

α

és

A

paraméter értékének kiszámítása során fel kell használnunk, hogy

\begin{matrix} x (t) & = exp (- K t) \cdot sin (Ω t - α), & (54a) \\ y (t) & = exp (- K t) \cdot cos (Ω t - α) & (55a) \end{matrix}

esetén

\begin{matrix} x' (t) & = - K \cdot exp (- K t) \cdot sin (Ω t - α) + exp (- K t) \cdot Ω \cdot cos (Ω t - α), & (54b) \\ y' (t) & = - K \cdot exp (- K t) \cdot cos (Ω t - α) - exp (- K t) \cdot Ω \cdot sin (Ω t - α); & (55b) \end{matrix}

illetve:

\begin{matrix} x (t) = y (t) + z (t) \end{matrix}

(56a)

és

\begin{matrix} u (t) = t \cdot exp (- K t) \end{matrix}

(57a)

esetén

\begin{matrix} x' (t) = y' (t) + z' (t) \end{matrix}

(56b)

és

\begin{matrix} u' (t) = (1 - K t) \cdot exp (- K t) . \end{matrix}

(57b)

Látható, hogy az (53) próbafüggvények a (18) próbafüggvénybe mennek át, ha

t ≫ τ_{max}

. A bekapcsolás után elég hosszú idővel tehát szinuszosan változó áram- és feszültségviszonyokkal számolhatunk.
Az (53) próbafüggvények a (3) egyenlet minden fizikai szempontból szóbajövő megoldását megadják, hiszen segítségükkel követni tudjuk az áram- és feszültségviszonyok alakulását bármely lehetséges bekapcsolási állapot esetén. Ezen túlmenően még azt is meg lehet mutatni, hogy (3)-nak nincsenek (53)-tól különböző megoldásai.
Meg lehet mutatni, hogy a váltóáramú áramköri egyenletek mindig megoldhatóak elegendően sok

A \cdot exp (- \frac{t}{τ})

A \cdot t \cdot exp (- \frac{t}{τ})

A \cdot sin (ω t - φ)

és

A \cdot exp (- \frac{t}{τ}) \cdot sin (Ω t - α)

függvény illesztésével, ha áramkörünket szinuszos váltóáramra kapcsoljuk. Az exponenciális kifejezések a bekapcsolás után elegendően hosszú idővel jelentéktelenné válnak; az áramkör stacionárius viszonyait a tiszta szinuszos tagok írják le.