Kezdőlap


Cím:	Az 1968. évi (2.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1968/november, 161 - 165. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. $30^{\circ}$ -os hajlásszögű lejtőn $m_{1} = 8$ kg tömegű, $10$ cm átmérőjű tömör henger tengelyéhez hozzá van kötve fonállal $m_{2} = 4$ kg tömegű tégla. (1. ábra.) Mekkora gyorsulással mozognak? A súrlódási együttható a tégla és a lejtő között $μ = 0, 2$ . A gördülő ellenállás és a csapágy súrlódása elhanyagolandó.

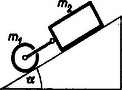1. ábra

I. megoldás. A henger alján

S

súrlódási erő működik (2. ábra).

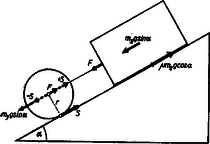2. ábra

A fonál

F

erővel húzza egymáshoz a hengert és a téglát. A henger középpontjában

m_{1} g sin α

, a tégla középpontjában

m_{2} g sin α

mozgató erő, a tégla alján

μ m_{2} g cos α

súrlódási erő működik (mert a tégla mozog). Az erők a rajz szerinti irányítások mellett pozitívok.
A tégla

a

gyorsulású egyenletesen gyorsuló mozgással mozog; Newton II. törvénye szerint:

\begin{matrix} m_{2} a = m_{2} g sin α + F - μ m_{2} g cos α . \end{matrix}

A henger középpontjában hozzáveszünk

\pm S

erőt. A henger középpontjának haladó mozgására igaz:

\begin{matrix} m_{1} a = m_{1} g sin α - F - S . \end{matrix}

I

tehetetlenségi nyomatékú henger

a / r

szöggyorsulással mozog; ez a szöggyorsulás egyenlő a forgatónyomaték és a tehetetlenségi nyomaték hányadosával:

\begin{matrix} \frac{a}{r} = \frac{S r}{I} . \end{matrix}

Három egyenletünk egyenletrendszert alkot, amelyet

a

-ra,

S

-re,

F

-re megoldva ezt kapjuk:

\begin{matrix} a = g \cdot \frac{(m_{1} + m_{2}) sin α - μ m_{2} cos α}{m_{1} + m_{2} + I / r^{2}}, & (1) \\ S = \frac{I}{r^{2}} \cdot g \cdot \frac{(m_{1} + m_{2}) sin α - μ m_{2} cos α}{m_{1} + m_{2} + I / r^{2}} & (2) \\ F = m_{2} g \cdot \frac{μ (m_{1} + I / r^{2}) cos α - I sin α / r^{2}}{m_{1} + m_{2} + I / r^{2}} & (3) \end{matrix}

Ha homogén hengerről van szó, akkor

I = m_{1} r^{2} / 2

és eredményeink:

\begin{matrix} a & = \frac{(m_{1} + m_{2}) sin α - μ m_{2} cos α}{1, 5 m_{1} + m_{2}} \cdot g, & (1') \\ S & = \frac{m_{1} g}{2} \cdot \frac{(m_{1} + m_{2}) sin α - μ m_{2} cos α}{1, 5 m_{1} + m_{2}} & (2') \\ F & = m_{2} g \cdot \frac{(1, 5 μ cos α - 0, 5 sin α) m_{1}}{1, 5 m_{1} + m_{2}} & (3') \end{matrix}

A feladatban szereplő számadatokkal:

\begin{matrix} a & = 0, 3317 g = 3, 252 {m/s}^{2}, & (1'') \\ S & = 1, 327 kp = 13, 005 newton, & (2'') \\ F & = 0, 020 kp = 0, 196 newton . & (3'') \end{matrix}

Tomasz KREGLEWSKI (Lengyelország)

II. megoldás. A szerkezet valamilyen

a

gyorsulással mozog és

t

idő alatt

a t^{2} / 2

utat tesz meg a lejtő mentén. Ezalatt a helyzeti energia csökkenése:

(m_{1} + m_{2}) g a t^{2} sin α / 2

. A haladásból származó összes mozgási energia:

(m_{1} + m_{2}) {(a t)}^{2} / 2

, a forgásból származó mozgási energia:

I ω^{2} / 2 = I v^{2} / 2 r^{2} = I {(a t)}^{2} / 2 r^{2}

(

ω

a szögsebesség,

r ω = v = a t

a kerületi sebesség). A súrlódási munka

μ m_{2} g cos α \frac{a}{2} t^{2}

. A mechanikai energiamegmaradás tétele szerint:

\begin{matrix} (m_{1} + m_{2}) g \cdot \frac{a}{2} \cdot t^{2} sin α = \frac{(m_{1} + m_{2})}{2} \cdot a^{2} t^{2} + \frac{I}{2 r^{2}} \cdot a^{2} t^{2} + μ m_{2} g cos α \cdot \frac{a}{2} \cdot t^{2} . \end{matrix}

Ennek megoldása

a

-ra az (1) alatti eredményt adja.

Mojmír SIMERSK

\overset{´}{Y}

(Csehszlovákia)

Taglalás. Vizsgáljuk meg, mikor indul el az összekötött szerkezet. Az elindulás feltétele, hogy

a > 0

legyen. A határesetben (1) alapján:

\begin{matrix} (m_{1} + m_{2}) sin α_{1} - μ m_{2} cos α_{1} = 0. \end{matrix}

Innen az elindulás határesetének feltétele:

\begin{matrix} tg α_{1} = μ \cdot \frac{m_{2}}{m_{1} + m_{2}} . \end{matrix}

A mi esetünkben

tg α_{1} = μ / 3 = 0, 0667

α_{1} = 3, 82^{\circ}

. (Külön a hengernél

α_{1} = 0^{\circ}

, külön a téglánál

α_{1} = arc  tg μ = 11, 31^{\circ}

lett volna az elindulás határhelyzete; a henger mintegy lehúzza a téglát.)
Az 1. feladatra mindeddig elmondottak csak akkor igazak, ha

F

pozitív, mert negatív

F

fonálerő nyomó igénybevételt jelentene, erre pedig a fonál nem képes. A határeset feltételét megkapjuk, ha

F

(3)

szerinti értékét

0

-val tesszük egyenlővé:

\begin{matrix} μ (m_{1} + I / r^{2}) cos α_{2} - I sin α_{2} / r^{2} = 0. \end{matrix}

Innen a fonál feszességének feltétele:

\begin{matrix} tg α_{2} = μ (1 + \frac{m_{1} r^{2}}{I}); \end{matrix}

(4)

hengernél:

\begin{matrix} tg α_{2} = 3 μ, \end{matrix}

(4')

illetve számadatainkkal:

\begin{matrix} tg α_{2} = 0, 6, α_{2} = 30, 96^{\circ} . \end{matrix}

(4'')

Feladatunkban majdnem elértük ezt a szöget, ezért olyan kicsiny a fonálerő.
Előfordulhat, hogy a henger megcsúszik. Ennek feltétele, hogy

S

elérje a lehetséges legnagyobb súrlódási erőt,

μ m_{1} g cos α_{3}

-at. (Feltesszük, hogy a hengerre és a téglára a csúszási súrlódási együttható azonos.) (2) alapján:

\begin{matrix} \frac{I}{r^{2}} \cdot g \cdot \frac{(m_{1} + m_{2}) sin α_{3} - μ m_{2} cos α_{3}}{m_{1} + m_{2} + I / r^{2}} = μ m_{1} g cos α_{3} . \end{matrix}

Innen a határeset feltétele:

\begin{matrix} tg α_{3} = μ (1 + \frac{m_{1} r^{2}}{I}) . \end{matrix}

Ez érdekes módon egyezik a fonálfeszesség (4) alatti feltételével, tehát

α_{2} = α_{3}

. E szög túllépése után megszűnik a fonálerő és a két test egymástól függetlenül mozog: a tégla csúszik, a henger forog és csúszik. (Ha a fonalat súlytalan pálcával pótolnánk, ebben nem jönne létre erő.)
Ha a lejtő meredeksége

α_{2} = α_{3}

-nál nagyobb, akkor a tégla és a henger középpontjának gyorsulása:

\begin{matrix} a = g (sin α - μ cos α), \end{matrix}

a henger alján működő súrlódási erő:

\begin{matrix} S = μ m_{1} g cos α, \end{matrix}

a forgás szöggyorsulása

β

és kerületi gyorsulása:

\begin{matrix} β r = μ \frac{m_{1} r^{2}}{I} \cdot g cos α . \end{matrix}

A 3. ábra mutatja a mozgás adatainak

α

-tól való függését feladatunk számadatai mellett.

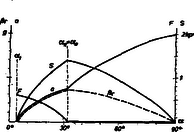3. ábra

TAKÁCS László (Magyarország)

2. feladat. Egyik pohárban

300 {c m}^{3}

0^{\circ} C

hőmérsékletű toluol, egy másik pohárban

110 {c m}^{3}

100^{\circ} C

hőmérsékletű toluol van. (Térfogatösszegük tehát

410 {c m}^{3}

.) Mennyi lesz az együttes térfogat, ha ezt a két folyadékot összeöntjük? A toluol köbös hőtágulási együtthatója

0, 001 {f o k}^{- 1}

. Minden hőveszteségtől tekintsünk el.

Megoldás. A

110 {cm}^{3}

100^{\circ}

-os toluol térfogata

0^{\circ}

-on (

β

hőkiterjedési együttható megadott számértékével visszaszámolva)

100 {cm}^{3}

. Így a tömegek aránya

3 : 1

és a keverés utáni hőmérséklet

25^{\circ} C

. A

400 {cm}^{3}

0^{\circ}

-os toluolnak

25^{\circ}

-on

410 {cm}^{3}

térfogata van. Az összeöntés által nem változott az összes térfogat. Felmerül az a gyanú, hogy ez szükségképp van így, nem véletlenség. Vizsgáljuk meg.
Ugyanazon folyadékból az egyik résznek

t_{1}

fokon

V_{1}

, a másik résznek

t_{2}

fokon

V_{2}

a térfogata. A

0^{\circ}

-ra visszaszámolt térfogatok:

V_{10} = V_{1} / (1 + β t_{1})

V_{20} = V_{2} / (1 + β t_{2})

. Ha

0^{\circ}

-on a sűrűség

d

, akkor a tömegek

m_{1} = V_{10} d

és

m_{2} = V_{20} d

. Az összekeverés utáni hőmérséklet:

\begin{matrix} t = \frac{m_{1} t_{1} + m_{2} t_{2}}{m_{1} + m_{2}} . \end{matrix}

Ezen a hőmérsékleten a térfogatok

V_{10} (1 + β t)

és

V_{20} (1 + β t)

.
Számítsuk ki a térfogatösszeget:

\begin{matrix} V_{10} (1 + β t) + V_{20} (1 + β t) = V_{10} + V_{20} + β (V_{10} + V_{20}) t = \\ = V_{10} + V_{20} + β \cdot \frac{m_{1} + m_{2}}{d} \cdot \frac{m_{1} t_{1} + m_{2} t_{2}}{m_{1} + m_{2}} = \\ = V_{10} + V_{20} + β (m_{1} t_{1} / d + m_{2} t_{2} / d) = V_{10} + β V_{10} t_{1} + V_{20} + β V_{20} t_{2} = \\ = V_{10} (1 + β t_{1}) + V_{20} (1 + β t_{2}) = V_{1} + V_{2} . \end{matrix}

Tehát a térfogatösszegnek állandónak kell maradnia. Több pohár esetében is így van, hiszen összeönthetünk először kettőt, ehhez a harmadikat és így tovább.

Peter GEORGIEV (Bulgária)

3. feladat.

\sqrt[]{2}

törésmutatójú üvegből fél henger készült. (

4

. ábra). Az üveg sík felületére

45^{\circ}

-os beesési szögben fénysugarakat bocsátunk. A fénysugarak a tengelyre merőleges metszet síkjában feküsznek. A henger palástjának mely részén lépnek ki fénysugarak?

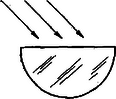4. ábra

Megoldás. Jellemezzük a fénysugár helyzetét a

φ

szöggel (5. ábra).

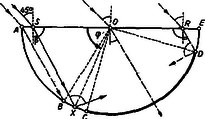5. ábra

A töréstörvény alapján:

\begin{matrix} \frac{sin 45^{\circ}}{sin β} = \sqrt[]{2}, sin β = \frac{1}{2}, β = 30^{\circ} . \end{matrix}

A törési szög az üvegben haladó valamennyi megtört fénysugárra nézve

30^{\circ}

. (A törésmutató

n = \sqrt[]{2}

.)
Azonnal látjuk, hogy

φ = 60^{\circ}

alatt geometriai okból nem érkezik fénysugár a hengerpalást belső felszínére.
A teljes visszaverődés határszöge

β_{t}

; erre nézve:

\begin{matrix} sin β_{t} = \frac{1}{n} = \sqrt[]{2}, β_{t} = 45^{\circ} . \end{matrix}

Minden fénysugár esetében

O S X ∢ = 60^{\circ}

. A teljes visszaverődés esetében

S X O ∢ > 45^{\circ}

, tehát

φ = 180^{\circ} - 60^{\circ} - 45^{\circ} = 75^{\circ}

az az érték, ameddig a palástot

B C

íven elérő fénysugarak teljesen visszaverődnek és nem lépnek ki. Amikor

φ

nagyobb lesz

75^{\circ}

-nál, kilép fénysugár a hengerpaláston.
Tovább haladva újból elérjük a teljes visszaverődés határesetét, amikor

O D R ∢

egyenlő lesz

45^{\circ}

-kal.

O R D ∢ = 120^{\circ}

, így

R O D ∢ = 180^{\circ} - 120^{\circ} - 45^{\circ} = 15^{\circ}

. Eszerint újból teljes visszaverődés kezdődik

φ = 180^{\circ} - 15^{\circ} = 165^{\circ}

-tól felfelé.
A hengerpaláston akkor lép ki fénysugár, amikor:

\begin{matrix} 75^{\circ} < φ < 165^{\circ} \end{matrix}

A kilépő sugarak

C D

ívéhez éppen

90^{\circ}

-os középponti szög tartozik.
Ki lehet mutatni, hogy a

B C

és

D E

ívhez tartozó, a paláston teljesen visszaverődő fénysugarak úgy érik el a felső sík lapot, hogy ott nem következik be teljes visszaverődés, tehát nem kell attól tartanunk, hogy ilyen teljesen visszaverődött sugarak valahol a hengerpalást egyéb részén kilépnek.

Emil MATEJEV (Bulgária)

Kísérleti feladat. Minden résztvevő három lezárt dobozt kapott, két áramkivezetéssel. Megállapítandó a doboz felnyitása nélkül, hogy milyen áramköri elemek vannak a dobozban és ezek elektromos jellemzőit meg kell mérni. Rendelkezésre áll két ,,Univo'' amper-voltmérő megadott mérési területekkel és belső ellenállásokkal, továbbá 10 voltos nagyságrendű egyenáramú, illetve 50-es frekvenciájú váltóáramú feszültségforrás. A műszerek egyenáramú mérés esetében

2 %

, váltóáramú mérés esetében

3 %

pontosságúak.

Megoldás. ,,A mérés megkezdése előtt meggyőződtem arról, hogy az egyes dobozok kapcsain nem mérhető saját feszültség.

I. doboz. Ohm törvénye alapján megmértem az ellenállást egyenárammal (

700

ohm

\pm 4 %

) és váltóárammal (

2200

ohm

\pm 6 %

). Tehát a doboz sorba kapcsolt ellenállást és induktivitást tartalmaz. Ohmos ellenállása

700

ohm. Induktív ellenállása

\sqrt[]{2200^{2} - 700^{2}} = 2070

ohm

\pm 8 %

, eszerint önindukciója

L = 2070 : 314 = 6, 6

henry

\pm 8 %

II. doboz. Az egyenáramú és váltóáramú mérés a hibahatárokon belül

3700

ohmot adott, tehát igen valószínű, hogy ekkora ohmos ellenállás van a dobozban.

III. doboz. Az egyenáramú mérés

30 000

ohm ellenállást adott. Mivel a dobozzal párhuzamos kapcsolásban használtam kb.

30 000

ohm ellenállású voltmérőt, nyilvánvaló, hogy a doboz saját ohmos ellenállása ennél sokkal nagyobb, gyakorlatilag elhanyagolható.
A váltóáramú mérés

6600

ohm

\pm 6 %

ellenállást adott. Tehát kondenzátorról van szó. Ennek kapacitása a

6600

ohm kapacitív ellenállásból számítva

C = 4, 9 μ F \pm 6 %

.''

MIHÁLY László (Magyarország)