Kezdőlap


Cím:	Testek gördülése, haladó és forgómozgás együttes fellépése II. Dinamikai jellemzés
Szerző(k):	Nagy László
Füzet:	1968/szeptember, 34 - 39. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A csúszásmentes gördülés dinamikai elemzése

Azzal az esettel foglalkozunk, melynek során a gördülő ellenállás elhanyagolható. Az előzőek értelmében a pillanatnyi forgástengely a gördülő testnek a felülettel érintkező alkotója, mely a testhez és a felülethez képest is időben változtatja helyzetét. Mivel a mozgás a pillanatnyi forgástengelyek körüli elemi forgásokból tevődik össze, ezért a pillanatnyi forgástengelyre bármely pillanatban az

M = Θ \cdot β

alapösszefüggés érvényes.

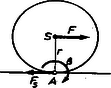1. ábra

Hasson

F

vízszintes erő a súlypontban (más esetekben értelemszerűen kell eljárni), ekkor az 1. ábra szerint

\begin{matrix} F \cdot r = Θ_{A} \cdot β, \end{matrix}

ahol

Θ_{A}

a testnek a pillanatnyi forgástengelyre vonatkozó tehetetlenségi nyomatéka. Ha ismerjük a testnek súlyponton átmenő tengelyre vonatkozó tehetetlenségi nyomatékát, akkor a vele párhuzamos,

r

távolságban levő tengelyre a tehetetlenségi nyomatékot Steiner tétele adja:

\begin{matrix} Θ_{A} = Θ_{S} + m \cdot r^{2} \end{matrix}

Behelyettesítéssel és

β \cdot t = a_{s}

figyelembe vételével^{$^{*}$}

\begin{matrix} F = \frac{Θ_{s} \cdot β}{r} + m \cdot a_{s} \end{matrix}

adódik. Tudjuk azonban azt, hogy nem pontszerű test esetén a testre ható erők eredője a test súlypontjának gyorsulását határozza meg. Jelenleg az

m g

gravitációs erő és az

F_{n}

alátámasztási erő eredője zérus, mert az összes többi szereplő erő vízszintes és a gyorsulás is vízszintes. Ezért ezek az erők a gyorsulás szempontjából figyelmen kívül hagyhatók. Így a dinamika alapegyenlete:

\begin{matrix} F - F_{s} = m \cdot a_{s} . \end{matrix}

Az előző képlettel összehasonlítva a tiszta gördüléshez szükséges súrlódási erő

\begin{matrix} F_{s} = \frac{Θ_{s} \cdot β}{r} = Θ_{s} \cdot \frac{a_{s}}{r^{2}} . \end{matrix}

Annál nagyobb súrlódási erőre van szükség, minél nagyobb gyorsulást akarunk a testen létrehozni. Ezt a súrlódási erőt vagy a nyugalmi súrlódás, vagy határesetben a tapadási súrlódás biztosítja, az

F_{s} \leq μ_{0} \cdot m \cdot g

összefüggés alapján adott gyorsulás esetén

\begin{matrix} μ_{0} > \frac{Θ_{s} \cdot a_{s}}{m \cdot g \cdot r^{2}} \end{matrix}

kell, hogy legyen. Az utóbbi egyenlőtlenség jobb oldalán levő érték* hengernél

\frac{1}{2} a_{s} / g

, gömbnél

\frac{2}{5} a_{s} / g

, abroncsnál

a_{s} / g

.
A vizsgált gördülést dinamikailag másképp is felfoghatjuk, ennek érdekében redukáljuk az. erőket a súlypontba (2. ábra).

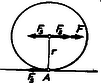2. ábra

Hasson még a testre a súlypontban egy

F_{s}

és egy

- F_{s}

erő (ezzel az erők eredőjét nem változtattuk meg). Rendezzük az erőket ezután egy a súlypontban ható

F - F_{s}

eredővé, melyről tudjuk, hogy a súlypont gyorsulását határozza meg, és egy

M = F_{s} \cdot r

forgatónyomatékú erőpárrá, melynek nyomatéka bármely tengelyre, tehát a súlyponton átmenő tengelyre is állandó. Ez a nyomaték állandó szöggyorsulást hoz létre. Az egyenletek, melyeknek egyidejűleg fenn kell állniuk, a következők

\begin{matrix} F - F_{s} & = m \cdot a_{s}, \\ F_{s} \cdot r & = Θ_{s} \cdot β \end{matrix}

Tehát a mozgás felfogható úgy, mint a súlypont egyenletesen gyorsuló haladó mozgása és a súlyponton átmenő tengely körüli egyenletesen gyorsuló forgómozgás. Ugyanúgy, mint ahogy sebességek esetében tettük, itt is látható*, hogy

β

ugyanakkora, mint a pillanatnyi forgástengely körüli szöggyorsulás, azaz a csúszásmentes gördülést jelenleg a

v_{s} = r \cdot ω

összefüggés helyett az a

a_{s} = r \cdot β

kinematikai egyenlettel tudjuk figyelembe venni. Az így nyert egyenletek természetesen az előző megoldás összefüggéseivel egyenértékűek, bármely meghatározásra váró mennyiségre ugyanezt az eredményt adják.*
Hogy a kétféle gondolkodás alkalmazásában gyakorlatra tegyünk szert, vizsgáljuk meg az

α

hajlásszögű lejtőn legördülő gömb esetét

(Θ_{s} = (2 / 5) \cdot m \cdot r_{2}) .

1. A pillanatnyi forgástengely körül a test forgómozgást végez (3. ábra).

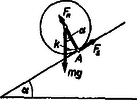3. ábra

Ebben az esetben

\begin{matrix} M_{A} = m \cdot g \cdot r \cdot sin α; \\ Θ_{A} = (2 / 5) \cdot m \cdot r^{2} + m \cdot r^{2} = (7 / 5) \cdot m \cdot r^{2}, \end{matrix}

így a szöggyorsulás

\begin{matrix} β = \frac{M_{A}}{Θ_{A}} = \frac{5 g sin α}{7 r} . \end{matrix}

A súlypont gyorsulása

\begin{matrix} a_{s} = β \cdot r = (5 / 7) \cdot g \cdot sin α . \end{matrix}

Az egyenletekben természetesen sem

F_{s}

, sem

F_{n}

nem szerepel, mivel ezek az erők

A

-n mennek keresztül, így nyomatékuk

A

-ra zérus. Ha a súrlódási erőt is ki akarjuk számítani, akkor a súlypont mozgására felírt mozgásegyenletet is fel kell használnunk. Mivel a súlypont gyorsulása, tehát a testre ható összes erő eredője és a súrlódási erő is lejtő irányú, ezért az

m g

gravitációs erő és az

F_{n}

alátámasztási erő eredője is lejtőirányú kell, hogy legyen. A jól ismert számolás alapján* ez az eredő

m g \cdot sin α

nagyságú, és a lejtőn lefelé mutat. Ugyanakkor

F_{n} = m g cos α

. Így a súlypont mozgására

\begin{matrix} m g \cdot sin α - F_{s} = m \cdot (5 / 7) g \cdot sin α, \end{matrix}

azaz

\begin{matrix} F_{s} = (2 / 7) \cdot m \cdot g \cdot sin α . \end{matrix}

A csúszásmentes gördülés feltétele

\begin{matrix} μ_{0} \geq F_{s} / F_{n} = (2 / 7) tgα. \end{matrix}

2. A súlypont gyorsuló mozgásához a súlyponton átmenő tengely körüli egyenletesen gyorsuló forgómozgás járul hozzá (4. ábra).

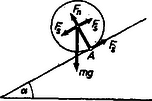4. ábra

A dinamika alaptörvényének egyenletei komponensenként (lejtőirányban és arra merőlegesen) az erőredukció után.

\begin{matrix} m \cdot g \cdot sin α - F_{s} = m \cdot a_{s}, \\ F_{n} - m \cdot g \cdot cos α = 0. \end{matrix}

A forgómozgás alapegyenlete:

\begin{matrix} F_{s} \cdot r = (2 / 5) \cdot m \cdot r^{2} \cdot β, \end{matrix}

és a csúszásmentességet biztosító kinematikai egyenlet

\begin{matrix} a_{s} = β \cdot r . \end{matrix}

Ezekből az egyenletekből a mozgás az előbbivel egyenértékűen vizsgálható.*

Gördülés csúszással

Nem tiszta gördülés jön létre például az 1. ábra esetében, ha

\begin{matrix} μ_{0} < \frac{Θ_{s} \cdot a_{s}}{m g \cdot r^{2}} . \end{matrix}

Ekkor a test csúszni fog, s a csúszási súrlódás

F_{s} = μ m g

értékét adottnak kell vennünk (

μ

a csúszási súrlódási együttható). Mivel most a testre ható összes erőt ismerjük (5. ábra), a súlypont gyorsulását meg akarjuk határozni.

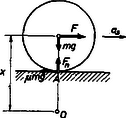5. ábra

\begin{matrix} F - μ m g = m \cdot a_{s} \end{matrix}

egyenletből:

\begin{matrix} a_{s} = \frac{F}{m} - μ g . \end{matrix}

A forgatónyomaték erőredukcióval

M = μ \cdot m \cdot g \cdot r

, tehát a szöggyorsulás

\begin{matrix} β = \frac{μ \cdot m g \cdot r}{Θ_{s}} . \end{matrix}

β

és

a_{s}

ismeretében a pillanatnyi forgástengely helyét a súlyponttól az

\begin{matrix} x = \frac{a_{s}}{β} = \frac{F / m - μ g}{\frac{μ \cdot m \cdot g \cdot r}{Θ_{s}}} \end{matrix}

összefüggés adja meg. Mivel

F > μ \cdot m \cdot g

, azért

x > 0

, vagyis a pillanatnyi forgástengely a súlypont alatt van. Ha a

\begin{matrix} μ < μ_{0} < \frac{Θ_{s} \cdot a_{s}}{m \cdot g \cdot r^{2}} \end{matrix}

összefüggést felhasználjuk,

x

-ről könnyű bebizonyítani* az

x > r

egyenlőtlenséget, vagyis a pillanatnyi forgástengely a testen kívül helyezkedik el.
A pillanatnyi forgástengelyt másképp is megkereshetjük. Ha ez a súlyponttól

x

távolságra van, mivel a tengely körül pillanatnyi forgás történik, akkor

\begin{matrix} F x - F_{s} (x - r) = (Θ_{s} + m x^{2}) β . \end{matrix}

A szöggyorsulás előbbi

β = μ m g r / Θ_{s}

értékével

x

-re a már megismert összefüggés adódik.*

Erőtani elemzés pillanatnyi forgástengely esetén

Egy dolgot az eddigiek szerint is világosan kell látnunk. A pillanatnyi forgástengely körüli elemi forgás esetén nem érvényes a forgómozgások dinamikájának az a tétele, hogy ,,tiszta'' forgómozgás esetén a testre ható erők eredője zérus, azaz a testre ható erők erőpárt alkotnak. Ez csak akkor áll fenn, ha a pillanatnyi forgástengely a gyorsuló mozgást nem végző súlyponton megy keresztül. A legutóbbi pillanatnyi forgástengely keresés esetén például

F

és

F_{s}

eredője sohasem lehet zérus (5. ábra).
A pillanatnyi forgástengely ismeretében bármely helyzetben (tehát nem az idő függvényében) elemi módszerekkel meg tudjuk határozni a súlypont gyorsulását.

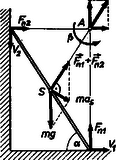6. ábra

A fal mellett súrlódásmentesen lecsúszó rudat vizsgálva újra, a 6. ábra szerint

F_{n 1}

és

F_{n 2}

átmegy a pillanatnyi forgástengelyen, ezért forgatónyomatékuk egyenként zérus. A gravitációs erő nyomatéka és a tehetetlenségi nyomaték:

\begin{matrix} M = m g \cdot (l / 2) cos α, \\ Θ_{A} = Θ_{s} + m {(\frac{l}{2})}^{2} = \frac{1}{12} m l^{2} + m {\frac{l}{4}}^{2} = \frac{1}{3} m l^{2} . \end{matrix}

A szöggyorsulás

\begin{matrix} β = {\frac{M}{Θ}}_{A} = \frac{3 g cos α}{2 l}, \end{matrix}

ezzel a súlypont gyorsulása

\begin{matrix} a_{s} = β \frac{l}{2} = \frac{3 g \cdot cos α}{4 l} . \end{matrix}

A testre ható három erő eredője

m \cdot a_{s}

, és mivel

m g

a súlypontban hat, kell, hogy

F_{n 1}

és

F_{n 2}

eredője is a súlyponton menjen keresztül. Ezért az adott helyzetben

F_{n 1}

és is

F_{n 2}

meghatározható*, s ezzel a dinamikai tárgyalás teljes.

Dinamikai jellemzés kijelölt forgástengely esetén

Vizsgáljuk meg a dinamikai tárgyalást olyan esetben, amikor kijelölt forgástengely van, de az nem megy át a súlyponton.
A vízszintesen elengedett rúd egyik végén átmenő, a rúdra merőleges tengely körül billenhet le. Határozzuk meg a súlypont gyorsulását és a tengelynek a testre gyakorolt kényszererejét a rúd egy adott helyzetében.

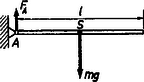7. ábra

Az egyszerűség érdekében tekintsük először a rúd vízszintes helyzetét (7. ábra).

A szöggyorsulás

\begin{matrix} β = \frac{M_{A}}{Θ_{A}} = \frac{3 g}{2 l}, \end{matrix}

a súlypont gyorsulása

\begin{matrix} a_{s} = \frac{l}{2} β = \frac{3}{4} g . \end{matrix}

A testre ható erők eredője Newton II. törvényéből

\begin{matrix} m g - F_{A} = m a_{s}, \end{matrix}

amiből

F_{A} = \frac{m g}{4}

adódik. Ha tehát az elengedés előtt a test a másik végen is alá volt támasztva, az

F_{A}

kényszererő az elengedés pillanatában az

m g / 2

értékről felére csökken. Ezt az erőcsökkenést mindenki érezheti, akinek társa egy gerenda másik végét elengedi.

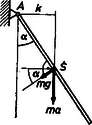8. ábra

Egy tetszőleges, a függőlegessel

α

szöget bezáró helyzetben (8. ábra)

\begin{matrix} M_{A} = m g \cdot \frac{l}{2} \cdot sin α . \end{matrix}

A szöggyorsulás

\begin{matrix} β = \frac{M_{A}}{Θ_{A}} = \frac{3 \cdot g \cdot sin α}{2 l}, \end{matrix}

és a súlypont érintőirányú (tangenciális) gyorsulása:

\begin{matrix} a_{s} = \frac{β \cdot l}{2} = \frac{3}{4} g sin α . \end{matrix}

A testre ható erők eredője, mely az érintőirányú gyorsulást létrehozza

\begin{matrix} F = m \cdot a_{s} = \frac{3}{4} m g sin α, \end{matrix}

mely erő a vízszintessel a szöget zár be. Az

m g

és

m \cdot a_{s}

ismeretében az

F

eredőkhöz hozzájáruló

F'_{A}

kényszererő meghatározható. Ha ehhez hozzávesszük még azt az erőt, mely az

A

pontban hat és iránya a súlyponton megy keresztül, amely erő a pillanatnyi centripetális gyorsulást biztosítja (látni fogjuk, hogy a súlypont sebességét a helyzet függvényében szintén ki tudjuk számítani elemi módszerekkel), akkor a centripetális erő és

F'_{A}

eredője a kívánt

F_{A}

csaperőt adja.

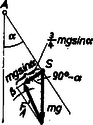9. ábra

A 9. ábra szerint*

\begin{matrix} F'_{A} = \frac{m g}{4} \sqrt[]{1 + 15 cos^{2} α} . \end{matrix}

Az egész problémát természetesen úgy is meg lehet oldani, hogy az erőket a súlypontba redukáljuk (hasonlóan a 4. ábrához). Ekkor belátható, hogy

F'_{A} x

forgatónyomatékú erőpár a súlypont körül éppen az előbbi szöggyorsulást hozza létre (

x

F'_{A}

hatásvonalának a súlyponttól való távolsága).

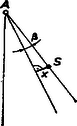10. ábra

Az ábra szerint a

β

-val jelzett szögre*

tgβ=\frac{1}{4}tg α

, továbbá a 10. ábra szerint*

\begin{matrix} x = \frac{l}{2} sin β = \frac{l}{2} \frac{tg α}{\sqrt[]{16 + {tg}^{2} α}}, \end{matrix}

ezzel a kérdéses erőpár nyomatéka

\begin{matrix} M_{s} = F'_{A} \cdot x . \end{matrix}

Ebből és a

β = M_{s} / Θ_{s}

, egyenletből

\begin{matrix} β = \frac{3 g \cdot sin α}{2 l} \end{matrix}

adódik.* Innen a feladat további elemzése már ismert.
A feladat világosan mutatja és összefoglalóul ezt kell hangsúlyoznunk, hogy ha a forgómozgás alapegyenletét a forgástengelyre írjuk fel, megkapjuk a szöggyorsulást és ebből a súlypont gyorsulását. A testre ható összes erő hatását azonban csak a súlypont mozgására vonatkozó dinamikai alapegyenlet adja meg. A másik lehetőség az, hogy az erőket a súlypontba redukálva felírjuk a dinamika alapegyenletét és a súlyponton átmenő tengelyre a forgómozgás alapegyenletét. Ekkor

a_{s}

és

β

között kapcsolatot az teremt, hogy van a testnek egy olyan pontja (ill. egyenese) ‐ ez a forgástengely ‐ melynek gyorsulása zéró.

^{$^{*}$}A következőkben is a csillaggal jelölt számításokat az olvasónak célszerű elvégeznie.