Cím:	Testek gördülése, haladó és forgómozgás együttes fellépése I.
Szerző(k):	Nagy László
Füzet:	1968/május, 225 - 228. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Kinematikai jellemzés   Testek gördülését szokás úgy tárgyalni, mint a súlypont haladó mozgásának és a súlyponton átmenő tengely körüli forgásnak együttes fellépését. Többek között ennek a szemléletnek a jogosságát vizsgáljuk mind kinematikai és dinamikai szempontból, mind egyszerűbb esetek energetikai elemzésével. Közben néhány olyan ismeretet is szerzünk, mely egyéb feladatok megoldása szempontjából is fontos. A szövegben csillaggal jelöltük meg azokra a számolásokra való utalásokat, melyeket szeretnénk, ha az olvasó saját maga végezne el. Csak síkbeli eseteket vizsgálunk, ami azt jelenti, hogy a test bármely pontjának sebessége merőleges a forgástengelyre. Eszerint például gördülő henger esetén elegendő valamely, a henger tengelyére merőleges sík pontjainak kinematikai viszonyait vizsgálnunk.   A pillanatnyi forgástengely   Egy test csúszásmentes gördülése azt jelenti, hogy egy adott felülettel, például egy síkkal érintkező pontjainak (az 1. ábrán $A$ pont) a felülethez viszonyított sebessége zérus. Henger esetén ezek a pontok a rajz síkjára merőleges alkotót adnak. Általában mindazon pontok által alkotott egyenest, melyeknek pillanatnyi sebessége zérus, pillanatnyi forgástengelynek nevezzük. A pillanatnyi forgástengely lehet a testen belül és a testen kívül is. A következőkben a pillanatnyi forgástengelynek a dinamikai és az energetikai elemzésnél is döntő szerepe lesz. 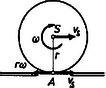    1. ábra   Az 1. ábrán látható csúszásmentes gördülést a következőképp állíthatjuk elő. Adjunk a testnek $v_s$ vízszintes sebességet, és ugyanakkor a $v_s$ sebességre merőlegesen álló szimmetriatengelye körül forgassuk meg akkora szögsebességgel, hogy az $A$ pontnak a haladó mozgásból származó $v_s$ és a forgómozgásból származó $r\cdot \omega$ kerületi sebessége egyenlő nagyságú és ellentétes irányú legyen. Ekkor az $A$ pont sebessége a vektori (jelenleg algebrai) összegezés folytán zérus és így betöltheti a pillanatnyi forgástengely szerepét. Eszerint a csúszásmentes gördülés feltétele: 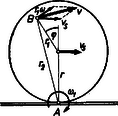$v_s=r\cdot \omega$.     2. ábra   A gondolatmenetből kitűnik, hogyan kell bármely pont pillanatnyi sebességét meghatározni. Legyen a gördülő test egy pontja a 2. ábrán jelölt $B$ pont, melynek a szimmetriatengelytől való távolsága $r_1$. Pillanatnyi sebességét az ábrán látható szerkesztés adja. Ugyanakkor a pont sebessége úgy is meghatározható, mint a pillanatnyi forgástengely körüli $r_2$ sugárral történő forgás kerületi sebessége. A kérdés csupán az, hogy mekkora a pillanatnyi forgástengely körüli forgás szögsebessége. Legyen ez ${\omega }_1$. A 2. ábra trigonometriai összefüggéseinek elemzésével általánosságban bizonyítható$*$, hogy ${\omega }_1=\omega$. Mint egyszerű esetet, vizsgáljuk meg a súlypont mozgását, melynek ismerjük $v_s$ sebességét. Ha ezt a pillanatnyi forgástengely körüli forgásból származtatjuk, akkor $v_s=r\cdot {\omega }_1$. Az előzőleg megállapított összefüggéssel összevetve $\omega ={\omega }_1$. Mielőtt ezen problémák taglalásában továbbhaladnánk, vizsgáljuk meg konkrét példán, hogyan kell a pillanatnyi forgástengely helyzetét és a szögsebességet megállapítani. A 3. ábrán látható rúd fal mellett csúszik le. 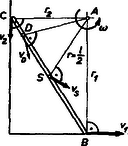    3. ábra   Bármely adott pillanatban ismerjük két végpontja sebességének irányát. Ha ezeket a sebességeket forgásból származtatjuk, akkor a pillanatnyi forgástengelyt a sebességekre merőleges egyeneseken kell keresnünk, mégpedig azok metszéspontján megy át ($A$ pont), s a szögsebesség előjelét egyértelműen meghatározza egy pont sebességének értelme. Egy tetszőleges $D$ pont sebességének iránya ás értelme ebből már adódik. A szögsebesség nagyságát kinematikai viszonyokból akkor tudjuk meghatározni, ha ismerjük a test valamely pontja sebességének nagyságát is. Ha például a $B$ pont sebessége $v_1$, akkor $\omega =v_1/r_1$. Az $\omega$ ismeretében a geometriai viszonyokból bármely pont sebességének nagysága is adódik, például a súlypont sebessége: $\begin{array}{c}{\displaystyle v_s=\omega \cdot r=\frac{v_1}{r_1}\cdot \frac{l}{2}\mathrm{.}}\end{array}$ Párhuzamos tengelyű forgások összetétele Vizsgáljuk meg, milyen jelentést adhatunk annak az esetnek, amikor egy testen két párhuzamos forgástengelyt jelölünk ki ${\omega }_1$ és ${\omega }_2$ szögsebességekkel (4. ábra).     4. ábra   Legyen a két tengely távolsága $d$. Ha az egyszerűség kedvéért a tengelyek síkjában levő $B$ pont sebességét megvizsgáljuk, mely a kijelölt tengelytől $r_1$ és $r_2$ távolságra van, akkor e pont mindkét forgásból származóan is sebességgel rendelkezik, s tényleges sebessége ezen sebességek eredője. $\begin{array}{c}{\displaystyle v_B=v_1-v_2=r_1{\omega }_1-r_2{\omega }_2\mathrm{.}}\end{array}$ Ezt az összefüggést az $r_2=r_1-d$ kapcsolat felhasználásával a további két alakban is felírhatjuk${}^{*}$: ${\displaystyle \begin{array}{c}\hfill {\displaystyle v_B=r_1\left({\omega }_1-{\omega }_2\right)+{\omega }_{2}d\mathrm{,}}\hfill \\ \hfill {\displaystyle v_B=r_2\left({\omega }_1-{\omega }_2\right)+{\omega }_{1}d\mathrm{.}}\hfill \end{array}}$ Mivel $r_1$ és $r_2$ változó lehet attól függően, hogy a test mely pontjának sebességét vizsgáljuk, ugyanakkor bármely pont esetén ${\omega }_1\cdot d$ és ${\omega }_2\cdot d$ adott, ezért mindkét összefüggés mutatja, hogy olyan mozgás jön létre, mely egy ${\omega }_1-{\omega }_2$ szögsebességű forgás és egy haladó mozgás összetétele. 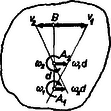    5. ábra   A haladó mozgást megadó rész éppen annak a tengelynek a sebessége, melyre az ${\omega }_1-{\omega }_2$ szögsebességű forgást vonatkoztatjuk. Például az $r_1\left({\omega }_1-{\omega }_2\right)$ az $A_1$ tengely körüli forgásból származó kerületi sebesség és ${\omega }_2\cdot d$ az $A_1$ pontnak az $A_2$ tengely körüli forgásból származó kerületi sebessége. Az előzőek szerint ebben az esetben is létezik pillanatnyi forgástengely, melynek pillanatnyi sebessége $0$, ezért $B$ pont sebessége e tengely körüli forgásból $\begin{array}{c}{\displaystyle v_B=r\left({\omega }_1-{\omega }_2\right)}\end{array}$ összefüggéssel számítható, ahol $r$ a pillanatnyi forgástengelynek a $B$ ponttól való távolsága. A számítást elvégezve${}^{*}$ (a $v_B$-re kapott két értéket összehasonlítva) az adódik, hogy a pillanatnyi forgástengely az $A_1$ ponttól $\begin{array}{c}{\displaystyle r-r_1=\frac{{\omega }_2}{{\omega }_1-{\omega }_2}\cdot d\mathrm{,}}\end{array}$ az $A_2$ ponttól $\begin{array}{c}{\displaystyle r-r_2=\frac{{\omega }_1}{{\omega }_1-{\omega }_2}\cdot d\text{távolságra van.}}\end{array}$ A feltételezés szerint (más esetekben értelemszerűen kell eljárni) ${\omega }_1>0$ és ${\omega }_2>0$ (mert előjelesen vettük figyelembe), továbbá ${\omega }_1>{\omega }_2$, ezért az $\begin{array}{c}{\displaystyle \frac{r-r_1}{r-r_2}=\frac{{\omega }_2}{{\omega }_1}}\end{array}$ összefüggés felhasználásával megállapítható${}^{*}$, hogy $r>r_1>r_2$. Ez nem is lehet másképp, mert az $A_2$ sebessége az $A_1$ körüli forgásból ${\omega }_1\cdot d$, továbbá $A_2$ és $A_1$ sebessége egyező értelmű. Ezért a pillanatnyi forgástengely jelenleg az $A_1$ és $A_2$ pontokat összekötő szakaszon kívül, $A_1$ oldalán van, mégpedig ott, mely pontra az előző összefüggés értelmében ${\omega }_{1}x={\omega }_2\left(d+x\right)$. Itt $x$ a pillanatnyi forgástengelynek az $A_1$-től való távolsága $\left(x=r-r_1;d+x=r-r_2\right)$.   A forgástengely-redukció A testek gördülése szempontjából bennünket különösen az az eset érdekel, amikor $|{\omega }_1|=|{\omega }_2|=\omega$, de a szögsebességek ellentétes előjelűek. Ekkor az eddigi egyenletek így módosulnak: $v_B=\omega \cdot d$ (bármely $B$ pontra), $x$ pedig nem véges${}^{*}$ (szokásos szóhasználat szerint a pillanatnyi forgástengely a végtelenben van). Az így előadódó esetet forgáspárnak nevezzük, és bármely pontra jelentését egy $\omega \cdot d$ nagyságú, a két tengely síkjára merőleges irányú haladó sebesség adja meg. A forgáspár módot ad arra, hogy úgynevezett forgástengely-redukciót hajtsunk végre, mely tiszta gördülés esetén a következő. Legyen a pillanatnyi forgástengely az $A$ pontban, és a szögsebesség $\omega$. Adjunk a mozgáshoz a súlyponti tengelyen átmenő $+\omega$ és $-\omega$ szögsebességű forgásokat, ezzel a test mozgásának hű leírását nem változtatjuk meg, mert e két forgásból bármely pont eredő sebessége $0$ (6. ábr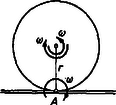a).     6. ábra   Az így előálló, most már három forgást egy forgáspárrá és egy súlyponti tengely körüli forgássá összevonva a forgáspárból $v_s=\omega \cdot r$ sebesség adódik, s bármely pont sebességét ezen haladó és a súlyponti tengelyen átmenő $\omega$ szögsebességből származó kerületi sebesség eredője adja. Visszajutottunk ezzel a gördülésre tett megállapításainkhoz. 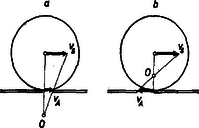    7. ábra   Ha nem tiszta gördülés esete áll fenn, hanem a testnek nyugvó felülettel érintkező pontja is sebességgel rendelkezik, akkor a sebesség irányától függően a 7a ábra szerint a pillanatnyi forgástengelyt a felület oldalán, a 7b ábra szerint a test oldalán kell keresnünk. Járművek kerekeinél mindkét eset előfordul.