Kezdőlap


Cím:	1967. évi Eötvös Loránd Fizikaverseny
Füzet:	1968/február, 81 - 85. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1967. október 21-én rendezte fizikai versenyét az 1967. évben érettségizettek számára. A versenyzők 5 órát dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

1. Ferde hajítással

X = 45 m

messze és

Y = 20 m

magasan levő célpontot kell eltalálni úgy, hogy az elhajított tárgy közben egy

x_{0} = 20 m

messze levő,

y_{0} = 15 m

magas akadály felett repül át. Milyen feltételnek tegyen eleget a kezdősebesség és az elhajlási szög, hogy ez sikerüljön ?

Megoldás. Keressük a pálya függvényét (1. ábra).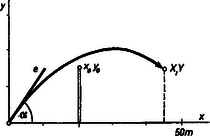

1. ábra

A ferde hajítás ismert törvénye szerint az elhajított tárgy koordinátái:

\begin{matrix} x = c cos α \cdot t, \\ y = c sin α \cdot t - \frac{g}{2} t^{2} . \end{matrix}

t

kiküszöbölésével kapjuk a pálya függvényét:

\begin{matrix} y = tg α \cdot x - \frac{g}{2 c^{2} cos^{2} α} \cdot x^{2} . \end{matrix}

Annak feltétele, hogy eltaláljuk az

X, Y

koordinátájú pontot, az, hogy

X, Y

kielégítse a fenti függvénykapcsolatot:

\begin{matrix} Y = tg α \cdot X - \frac{g}{2 c^{2} cos^{2} α} \cdot X^{2} . \end{matrix}

Ez feltételt szab meg

c

indítási sebességre és

α

indítási szögre, ez a feltétel:

\begin{matrix} c = \sqrt[]{\frac{g X^{2}}{2 cos^{2} α (X tg α - Y)}} . \end{matrix}

(1)

X, Y

pont eltalálásának ezt a feltételét grafikusan ábrázolhatjuk, ha feltüntetjük az

α

c

koordinátarendszerben azokat a pontokat, amelyek (1) feltételnek megfelelnek. A görbét,

g = 10 {m/s}^{2}

érték felhasználása mellett a 2. ábra tünteti fel folytonos vonallal.

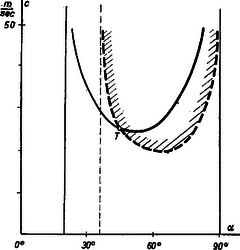2. ábra

Ez a görbe a

18, 7^{\circ}

-nál és

90^{\circ}

-nál rajzolt függőlegesek között helyezkedik el; általában adott sebesség mellett két szög esetében teszi lehetővé a cél eltalálását, kivéve az

54, 2^{\circ}

-nál és

24, 9 m/s

-nál levő minimumot.
Hasonlóan írhatjuk fel annak feltételét, hogy a lövedék eltalálja az akadály felső szélén levő,

x_{0}, y_{0}

koordinátájú pontot:

\begin{matrix} c = \sqrt[]{\frac{g x_{0}^{2}}{2 cos^{2} α (x_{0} tg α - y_{0})}} . \end{matrix}

(2)

E feltételt a 2. ábrán a szaggatott vonal tünteti fel; amely

36, 9^{\circ}

és

90^{\circ}

között helyezkedik el és minimuma

65, 6^{\circ}

-nál,

20 m/s

-nál van.
Az (1) és (2) feltételeket jelentő görbék metszéspontja

T

-ben van,

47, 3^{\circ}

-nál és

25, 5 m/s

-nál. Ha ezekkel az adatokkal végezzük el a hajítást, akkor az elhajított tárgy érinti az akadály felső szélét és eltalálja a célpontot. De az akadály felső szélét nem kell eltalálni, a tárgy elrepülhet felette, ezért feladatunk csak azt kívánja hogy

c

és

α

a 2. ábra vonalkázott görbéje felett legyenek. De az (1) feltétel betartása is kötelező, hogy eltaláljuk a célpontot. Ezért a feladat megoldása:

c

sebesség és

α

szög úgy választandó, hogy az (1) feltételnek tegyenek eleget, de

c

25,5 m/s

-nál és

α

47, 3^{\circ}

-nál nagyobb legyen, vagyis a

c

és

α

adatokat jelentő pontok a 2. ábra vastagított görberészén feküdjenek.

120 cm

hosszú csillagászati távcső tárgylencséje

100 cm

fókusztávolságú és

84 mm

átmérőjű gyűjtőlencse, szemlencséje

20 cm

fókusztávolságú és

12 mm

átmérőjű gyűjtőlencse. Mekkora az égboltból látható terület szögátmérője ?

Megoldás. A lencsék fókuszai egybeesnek. Először tekintsük a tengellyel párhuzamosan beeső, párhuzamos sugárnyalábot (3. ábra felső rajza).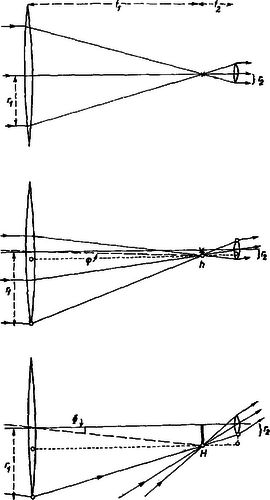

3. ábra

Ha a kilépő nyaláb teljesen megtölti a szemlencse területét, akkor a tárgylencsén

30

mm rádiuszú kör területén át esik be. Ha a beeső nyaláb sugarai egymás között párhuzamosak maradnak, de a nyaláb ferde szögben esik be a tengelyhez képest, akkor a fókuszsíkban fekvő találkozási pont kikerül a tengelyből. Egy bizonyos

φ

szög esetében a tárgylencse alsó szélén bemenő sugár a szemlencse felső szélén távozik (3. ábra középső rajza). Ez az a legferdébb nyaláb, amelynek sugarai még hiánytalanul átjutnak a távcsövön. Az ábrán köröcskékkel vannak megjelölve hasonló háromszögek csúcspontjai; ezekből a háromszögekből:

\begin{matrix} \frac{h + r_{2}}{f_{2}} = \frac{r_{1} - h}{f_{1}} . \end{matrix}

Itt

h

jelenti a közbeeső kép nagyságát. Innen:

\begin{matrix} h = \frac{f_{2} r_{1} - f_{1} r_{2}}{f_{1} + f_{2}} . \end{matrix}

A látószög (fele) radiánban:

\begin{matrix} φ = \frac{h}{f_{1}} = \frac{f_{2} r_{1} - f_{1} r_{2}}{f_{1} (f_{1} + f_{2})} . \end{matrix}

(3)

Számadatainkkal

φ = 0, 002 rad = 0, 114^{\circ} = 6, 84'

, illetve

2 φ = 0, 004 rad = 0, 228^{\circ} = 13, 68'

.
Ha a beérkező nyaláb tengellyel alkotott hajlásszöge még nagyobb lesz, akkor a szemlencsén kilépő, illetve kilépésre képes nyalábból mindig kevesebb tud bejutni a tárgylencse területén át. Ha a hajlásszög

Φ

értéket éri el, akkor a tárgylencse alsó szélén át bejutó sugár a szemlencse alsó széle felé halad (3. ábra alsó rajza). Ennél nagyobb hajlásszög mellett egyetlen sugár sem képes a távcsövön keresztüljutni.

H

a közbeeső kép nagyságát jelenti. A köröcskékkel megjelölt hasonló háromszögekből:

\begin{matrix} \frac{H - r_{2}}{f_{2}} = \frac{r_{1} - H}{f_{1}} \end{matrix}

innen:

\begin{matrix} H = \frac{f_{2} r_{1} + f_{1} r_{2}}{f_{1} + f_{2}} . \end{matrix}

A látószög (fele) radiánban:

\begin{matrix} Φ = \frac{H}{f_{1}} = \frac{f_{2} r_{1} + f_{1} r_{2}}{f_{1} (f_{1} + f_{2})} . \end{matrix}

(4)

Számadatainkkal

Φ = 0, 012 rad = 0, 6875^{\circ} = 41, 25'

, illetve

2 Φ = 0, 024 rad = 1, 375^{\circ} = 1^{\circ} 22, 5'

.
Tehát a feladat megoldása a következő. Amíg az érkező nyaláb hajlásszöge kisebb, mint a (3) által megadott

φ

-érték, addig a látómező változatlan fényességű. Ezt körülveszi a (4) által megadott

Φ

-ig egy körgyűrű, amelynek területén a fényerősség folyamatosan csökken. A

Φ

által megszabott körön kívül semmit sem látni. A valóságban a fókuszpontok találkozási helyén elhelyezett körgyűrű alakú rekesszel tartják távol azokat a sugarakat, amelyek már nem adnak megfelelő világosságú képet. Ha a rekesz a gyújtópontok találkozási síkjában áll, akkor szélét élesen látjuk.

3. Vasmagot két sokmenetű tekercseléssel látunk el, amelyek menetszáma egyenlő, de menetiránya ellentétes (4. ábra). A tekercseket egy-egy

R

ohmos ellenállással sorba kapcsoljuk, azután az egyiket

U = 100 volt

állandó egyenfeszültségre kapcsoljuk. Hosszabb idő múlva

K

kapcsoló zárásával a másik ágat is rákapcsoljuk az

U

feszültségre. Közvetlenül

K

bekapcsolása után (néhány ezred-másodperc múlva) mekkora mindegyik ág áramerőssége ?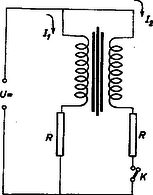

4. ábra

Megoldás. Állapodjunk meg abban, hogy a 4. ábrán feltüntetett áramirányokat tekintjük pozitívoknak. Az 5. ábra a két áramerősség és a vasmag mágneses fluxusát tünteti fel mint az idő függvényét.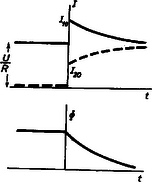

5. ábra

K

kapcsoló bekapcsolása előtti időben az első áramerősség

I_{1} = U / R

(folytonos vonal), a második

I_{2} = 0

. A bekapcsolás után igen hosszú idő múlva

I_{1} = U / R

és

I_{2} = U / R

. A kapcsoló bekapcsolása után közvetlenül az áramerősségek

I_{10}

és

I_{20}

. Ezeket keressük.
A tekercsekben folyó áram a vasmagban mágneses fluxust hoz létre, amely arányos az áramerősséggel:

Φ = k I

. Mágneses fluxusnak nevezzük a vasmagban található összes mágneses indukcióvonal számát. A kapcsoló üzemeltetéséig a vasmagot csak az első áram mágnesezi, és ezért

Φ = k I_{1} = k \cdot \frac{U}{R}

. A kapcsolás után igen hosszú idő múlva a második áram erőssége is

U / R

, de ez az áram a vasmagot ellentétesen mágnesezi, ezért igen hosszú idővel a kapcsolás megtörténte után a fluxus nulla (5. ábra alsó rajza).
A kapcsolás pillanatában folyó

I_{10}

és

I_{20}

áramok ellentétes irányúak, ezért ekkor a fluxus:

k I_{10} - k I_{20}

. Az önindukció jelenségének az a lényege, hogy a mágneses fluxus hirtelen nem ugorhat egy véges értékkel, ezért a kapcsolás előtt és közvetlenül utána a fluxusnak egyenlőnek kell lennie:

\begin{matrix} k \cdot \frac{U}{R} = k I_{10} - k I_{20} . \end{matrix}

Innen egyenletet kapunk az áramerősségek különbségére:

\begin{matrix} I_{10} - I_{20} = \frac{U}{R} . \end{matrix}

(5)

A kapcsolás után a fluxus folyamatosan csökkenni kezd, hiszen hosszú idő múlva értéke nulla. A fluxus csökkenése a tekercsek közös vasmagjában feszültséget indukál mindegyik tekercsben, amelynek nagysága mindegyik tekercsben

L k \cdot d Φ / d t = U_{i}

és irányítása olyan, hogy a fluxus csökkenésének ellene szegül. Ez az indukált feszültség hozzájárul az eredeti feszültséghez, de az ellentétes menetirányok folytán különböző előjellel. Ohm törvénye szerint:

\begin{matrix} U + U_{i} = R I_{10}, \\ U - U_{i} = R I_{20} . \end{matrix}

Ezeket összegezve

2 U = R (I_{10} + I_{20})

, tehát egyenletet kaptunk az áramok összegére:

\begin{matrix} I_{10} + I_{20} = \frac{2 U}{R} . \end{matrix}

(6)

Az (5)-ből és (6)-ból álló egyenletrendszert megoldjuk

I_{10}

és

I_{20}

ra:

\begin{matrix} I_{10} & = \frac{3}{2} \cdot \frac{U}{R}, \\ I_{20} & = \frac{1}{2} \cdot \frac{U}{R} . \end{matrix}

Ez a feladat megoldása. Az indukált feszültségre azt kapjuk, hogy

U_{i} = U / 2

. Az áramok függését az időtől az 5. ábra felső rajza tünteti fel.

A verseny eredménye. A bíráló bizottság az első díjat nem adta ki. A második és harmadik díjat összevonva, egyenlő arányban megosztva hárman kapták meg: Kádas Sándor (a budapesti tudományegyetem fizikus hallgatója, tavaly a budapesti József Attila gimnáziumban Honfi Lászlóné tanítványa), Szalay Sándor (a debreceni tudományegyetem fizikus hallgatója, tavaly a debreceni egyetemi gyakorló gimnáziumban Trón Lászlóné tanítványa), Szűcs Pál (a budapesti tudományegyetem fizikus hallgatója, tavaly a budapesti Fazekas Mihály gimnáziumban Kőváry Károly tanítványa). A versenyen részt vevő gimnáziumi tanulók közül kitüntető jutalmat kapott Diósi Lajos, a budapesti Apáczai Csere János gimnázium IV. osztályában Csernák Emil tanítványa.