Kezdőlap


Cím:	Kérdezz - felelek!
Szerző(k):	Major János
Füzet:	1968/január, 33 - 36. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kérdés: A 702. feladat megoldásánál szükségünk volt az eredő forgatónyomatékra. Nem látjuk világosan, hogyan kell értelmezni ezt a fogalmat. (Több megoldó).

Felelet¹. Foglalkozzunk a feladat megoldása előtt azzal, hogy pontosan mit értünk eredő erőn, illetve forgatónyomatékon.
A vektor geometriai definíciója: irányított egyenes szakasz megadott műveleti szabályokkal. Ezek a műveleti szabályok (l. Dózsa Márton cikkét: K. M. L. 33. kötet 159. lap):
1. Két vektor azonos, ha egymásba párhuzamos eltolással átvihető.
2. Két vektor összegét a paralelogramma módszerrel kaphatjuk meg: a második vektort úgy toljuk el önmagával párhuzamosan, hogy kezdőpontja egybeessen az első vektor végpontjával. Ekkor az első vektor kezdőpontjától a második vektor végpontjáig húzott egyenes szakasz definíció szerint a két vektor összege.
3. Valós számmal való szorzás (jelöljük a valós számot

α

-val): a vektor hosszát

α

-szorosára változtatjuk, ha

α \geq 0,

, és

(- α)

-szorosára, ha

α < 0

, de ekkor a vektor irányát ellentétesre kell változtatni.
4. Két vektor skaláris szorzata szám: (a művelet szokásos jele

a \cdot b

vagy ab) a két vektor hosszának és a közbezárt szög koszinuszának szorzata

(ab = a \cdot b \cdot cos φ)

.
5. Két vektor vektoriális szorzata vektor, mely merőleges a két vektor által kifeszített síkra (a művelet szokásos jelölése a

\times

b, az a, b, a

\times

b vektorok (ilyen sorrendben) jobb rendszert alkotnak; hossza a két vektor hosszának és a közbezárt szög szinuszának szorzata

(| a \times b | = | a | \cdot | b | sin φ)

.
Az elmozduláson kívül vektorra fizikai példa a sebesség, gyorsulás, erő, elektromos térerősség és még egy sor fizikai mennyiség.
Eddig nem beszéltünk támadási pontról. Azért, hogy ezt a fogalmat bevezethessük, foglalkoznunk kell a merev test egyensúlyának problémájával. Ismerjük Newton II. Törvényét:

m a = P

, ahol P a tömegpontra ható erő, a a tömegpont gyorsulása és

m

a tömege. A merev test egyensúlyának feltételét úgy vezethetjük le, hogy a merev testet sok tömegpontból állónak tételezzük fel. Például a merev test atomjait külön tömegpontoknak tekintjük. Jelöljük a merev test

i

-edik tömegpontjára ható külső (pl. gravitációs) erőt

P_{i}

-vel, a

j

-edik tömegpontnak az

i

-edikre ható erejét

F_{i j}

-vel (ezek az erők, az ún. belső erők tartják össze a testeket, és Newton III. törvénye szerint

F_{i j} = - F_{j i}

, valamint feltételezhetjük, hogy

F_{i j}

a két atomot összekötő egyenessel párhuzamos (centrális erő). Így fel tudjuk írni az (

m_{i}

tömegű,

a_{i}

gyorsulású)

i

-edik atom mozgásegyenletét:

\begin{matrix} m_{i} a_{i} = P_{i} + \sum_{j}^{} F_{i j}, \end{matrix}

ahol az összegzés az összes többi atomra kiterjed. Ezt az egyenletet a merev test összes tömegpontjára felírhatjuk. Most adjuk össze az összes ilyen egyenletet:

\begin{matrix} \sum_{i}^{} m_{i} a_{i} = \sum_{i}^{} P_{i} + \sum_{i}^{} \sum_{j}^{} F_{i j} . \end{matrix}

Az egyenlet bal oldala éppen a súlypont gyorsulása szorozva az egész test tömegével: a jobb oldal első tagja

P = \sum_{i} P_{i}

, a testre ható összes külső erő összege; második tagja, melyben minden

F_{i j}

mellett a megfelelő

F_{j i} = - F_{i j}

is szerepel, nulla.
Így tehát a merev test egyensúlyának első feltétele (egyensúly esetén a gyorsulások nullák):

\begin{matrix} \sum_{i}^{} P_{i} = 0, \end{matrix}

vagyis a testre ható külső erők összege nulla.
Az egyensúly második feltételét úgy kapjuk meg, hogy az

i

-edik tömegpont mozgásegyenletét vektoriálisan megszorozzuk

r_{i}

-vel, a tömegpont helyvektorával (az origótól a tömegpontig húzott vektorral):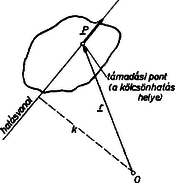

\begin{matrix} m_{i} r_{i} \times a_{i} = r_{i} \times P_{i} + \sum_{j}^{} r_{i} \times F_{i j} . \end{matrix}

Ismét összegezzünk (mint az előbb)

i

-re:

\begin{matrix} \sum_{i}^{} m_{i} r_{i} \times a_{i} = \sum_{i}^{} r_{i} \times P_{i} + \sum_{i}^{} \sum_{j}^{} r_{i} \times F_{i j} . \end{matrix}

A bal oldal a test impulzusmomentumának nevezett fizikai mennyiség időbeli változását fejezi ki, esetünkben ez a tag nulla (egyensúly); a jobb oldal második tagja szintén nulla (bizonyítása az előzőekhez hasonlóan történik, felhasználva a belső

F_{i j}

erők centrális voltát), az egyensúly feltétele tehát

\begin{matrix} \sum_{i}^{} r_{i} \times P_{i} = 0. \end{matrix}

Az összeget úgy kell kiszámítani, hogy a testre ható erőket vektoriálisan megszorozzuk annak a helynek a helyvektorával, amelyik helyen az ,,erő hat'', és ezen vektorokat össze kell adni. A testek kölcsönhatását nemcsak az erő jellemzi (pl. mekkora és milyen irányú a kötélerő), hanem azt is meg kell mondani, hogy a két test kölcsönhatásának hol van a helye (pl. hol van a testre rákötve a kötél). Ezek után az erőnek a testre gyakorolt hatását a következő adatokkal jellemezhetjük: milyen nagyságú és irányú a hatás (erő, P); hol van a kölcsönhatás (támadási pont, helyvektora r). A támadási pont tehát nem az erő jellemzője, hanem az erővel együtt jellemzi a kölcsönhatást. Az erő forgatónyomatékán az

r \times P

vektoriális szorzatot értjük (1. ábra).

1. ábra

Visszatérhetünk alapproblémánkra: a

\sum_{i} r_{i} \times P_{i}

összeg nem más, mint a testre ható külső erők forgatónyomatékának összege. Így az egyensúly második feltétele:

\begin{matrix} \sum_{k}^{} M_{k} = 0. \end{matrix}

(Az összegben a testre ható valamennyi erő forgatónyomatéka szerepel.)
Ezt a feltételt egyszerűbben is fel lehet írni, ha a testre ható erők támadási pontjai (a kölcsönhatás helyei) egy síkban vannak, és az erők ezen síkkal párhuzamosak (a középiskolában előforduló legtöbb feladat ilyen). A vektoriális szorzat definíciója szerint ui. az összes forgatónyomaték vektor merőleges lesz erre a síkra, vagyis egymással párhuzamosak lesznek. Párhuzamos vektorok összeadása különösen egyszerű: a vektorok abszolut értékének (nagyságának) algebrai összege lesz az eredő abszolut értéke, figyelembe véve az előjelet, vagyis hogy a síkra merőleges vektor ,,lefelé'' vagy ,,felfelé'' mutat-e (ahogy mondani szokták: a pozitív irányba forgató erő nyomatéka pozitív és a negatív irányba forgatóé negatív, vagy éppen fordítva). Az egyensúly feltétele ,,egy síkban ható'' erők esetén:

\begin{matrix} \sum_{k}^{} M_{k} = 0. \end{matrix}

M_{k}

forgatónyomatékot a vektoriális szorzat fenti definíciójának megfelelően úgy kell kiszámítani, hogy párhuzamos egyenest rajzolunk a támadási ponton keresztül az erővel (hatásvonal), majd az origónak és ezen egyenesnek a (merőleges) távolságát (az erő karját) megszorozzuk az erő nagyságával (1. ábra).

Összefoglalva: a merev test egyensúlyának feltétele: a testre ható erők vektor‐összege nulla és a testre ható erő forgatónyomatékainak algebrai összege nulla, ha a testre csak egy síkban hatnak erők, a fenti értelemben. A továbbiakban csak egy síkban ható erőkkel fogunk foglalkozni.

Eddig nem beszéltünk a vonatkoztatási pont ‐ origó helyéről. Könnyen bebizonyítható, hogyha egy merev testre az egyensúly első feltétele teljesül és a forgatónyomatékok algebrai összege a tér valamely pontját origónak tekintve nulla, akkor biztosan nulla a tér tetszőleges más pontját tekintve origónak. Így az egyensúlyi feltételek felírásánál teljesen mindegy, hogy a tér melyik pontját választjuk vonatkoztatási pontnak. Egy másik pontot választva nem kapunk az eddigiektől független egyenletet.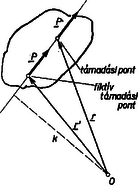

2. ábra

Láttuk tehát, hogy a merev test egyensúlyának feltételében nem szerepel a kölcsönhatás helye (az r helyvektor), csak a hatásvonalnak az origótól mért távolsága (az erő karja). Ha a testre ható P erő támadási pontját a hatásvonal mentén eltoljuk, de az erőt nem változtatjuk meg (2. ábra) (pl. a testre kötött kötelet a test egy megfelelő helyzetű másik pontjára kötjük át, és továbbra is ugyanolyan nagyságú és irányú erővel húzzuk, mint eddig), az egyensúly feltételei sem változnak meg. Az erő változatlan marad (az első feltételben csak az erő szerepel); a második feltételben az erő forgatónyomatéka szerepel, ám ez sem változik, mivel az erő és az erő karja is változatlan marad.

Az eddigiek alapján világos, hogy az egyensúly első feltételének felírásakor két erő helyett a vektorösszegüket is beírhatjuk, de ezt nem tudjuk megtenni a második feltételnél, mivel ebben szerepel a kölcsönhatás helye, a támadási pont is. A középiskolában tanult erőösszegzési eljárások azonban megadnak egy fiktív támadási pontot (helyvektora

r'

) (3.ábra), amely ugyan nem kölcsönhatási hely, de ha a két kölcsönhatást ezen fiktív támadási pontú eredő erővel

(P = P_{1} + P_{2})

helyettesítjük, ezen fiktív kölcsönhatás minden szempontból helyettesíti a két eredeti kölcsönhatást.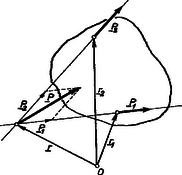

3. ábra

Ez az eredő kölcsönhatás nem egy igazi kölcsönhatás, ami onnan is látszik, hogy a támadási pontja nincs feltétlenül a testen. Tehát a fiktív kölcsönhatásban szereplő erő a két erő vektorösszege, és a fiktív kölcsönhatásban szereplő erők forgatónyomatéka egyenlő a két kölcsönhatásban szereplő erő forgatónyomatékának összegével a tér bármelyik pontját választva origóul.
Egyetlen probléma a fiktív támadási pont helyének meghatározása. A 702. feladatban annak a bizonyítása volt a feladat, hogy a középiskolában megismert módszerek helyesek a fenti szempontból. Így két nem párhuzamos, ,,egy síkban fekvő'' erő eredőjének fiktív támadási pontja a fentebb pontosan definiált hatásvonalak metszéspontja; párhuzamos erőkre pedig az ismert kissé bonyolultabb szerkesztési eljárás által megadott pont.
Végül vizsgáljuk meg kicsit részletesebben az erőpárt! Ha egy merev test egyik pontja

(r_{1})

egy P erő támadási pontja és egy másik pontja

(r_{2})

egy

- P

erőé, akkor a merev testre erőpár hat (4. ábra).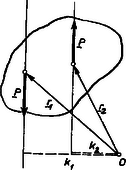

4. ábra

Az erőpár eredője:

\begin{matrix} P + (- P) = 0, \end{matrix}

azonban az eredő forgatónyomaték

k_{1}

hez a P-hez tartozó,

k_{2}

- P

-hez tartozó erőkar)

\begin{matrix} M = P k_{1} - P k_{2} = P (k_{1} - k_{2}) \end{matrix}

nem nulla, ha a két hatásvonal nem azonos. Tehát a merev testre ható két ilyen hatást nem helyettesíthetünk egyetlen (fiktív támadási pontú) erőhatással, mert a nulla nagyságú erő (a két erő eredője) forgatónyomatéka mindig nulla. Erőpár esetében nem beszélhetünk egyetlen eredő (fiktív) kölcsönhatásról, amely minden szempontból (a forgatónyomatékok szempontjából is) helyettesítené a két eredeti kölcsönhatást. Az egyensúly első feltételének felírásakor (ebben nem szerepel forgatónyomaték) az erőpár helyett mindig beírhatjuk az eredő erőt, azaz nullát. (A második feltételnél ezt természetesen nem tehetjük meg, mivel nincs fiktív [eredő] támadási pont.)

Első olvasáskor a cikkben szereplő levezetések kihagyhatók.
A cikket kollektív feldolgozásra ajánljuk középiskolai fizika szakköröknek. A szerző szívesen válaszol az esetleges problémákat, észrevételeket tartalmazó levelekre, melyeket a szerkesztőség címére lehet küldeni.

¹ A feladatot I. ugyanezen szám 46. oldalán.