Kezdőlap


Cím:	Az inverzióról
Szerző(k):	Surányi János , Tusnády Gábor
Füzet:	1968/november, 97 - 101. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1598. feladat II. megoldása¹ egy geometriai transzformációt használt fel, ami ‐ az ott szereplő számadatoktól függetlenül ‐ a következőképpen írható le:
Adott a síkon egy $C$ pont és egy $r$ távolság. Minden a $C$ -től különböző $R$ ponthoz a $C R$ félegyenesnek azt a $P$ pontját rendeljük hozzá, amelyre

\begin{matrix} C P \cdot C R = r^{2} . \end{matrix}

C

-nek nincs képe és nem is képe egy pontnak sem.
Világos, hogy ennél a leképezésnél fordítva is,

P

képe

R

, és hogy a

C

középpontú,

r

sugarú

k

kör pontjai egybeesnek a képükkel, a kör belsejében levő pontok képe a körön kívül van és viszont. Ezt a leképezést a

k

körre vonatkozó inverziónak vagy tükrözésnek szokás nevezni. Ismerkedjünk meg vele kicsit közelebbről.
A definíció szerint a

C

-ből induló félegyenesek (

C

-t nem számítva hozzájuk) az önmaguk képei, de csak egy-egy olyan pontjuk van, amely a saját képe; a

C

középpontú körök egy ugyanilyen körbe mennek át (de közülük csak

k

megy át önmagába).
A továbbiakban gyakran használjuk fel a következő segédtételt:
Ha az

R_{1}

R_{2}

pontok képe

P_{1}

P_{2}

, és az

R_{1} R_{2}

egyenes nem megy át

C

-n, akkor a

C P_{1} P_{2}

és a

C R_{2} R_{1}

háromszög hasonló (1. ábra).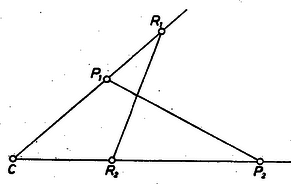

1. ábra

Valóban,

C P_{1} \cdot {C R}_{1} = r^{2} = C P_{2} \cdot {C R}_{2}

, amiből a következő arányok egyenlőségét kapjuk:

\begin{matrix} \frac{C P_{1}}{C P_{2}} = \frac{C R_{2}}{C R_{1}}, \end{matrix}

továbbá a két háromszög

C

-nél levő szöge közös. Ebből következik a segédtétel állítása. A két háromszög megadott körüljárási iránya ellentétes. (Ez magyarázza a tükrözés elnevezést is.)
Megmutatjuk, hogy
a) minden egyenes képe, amelyik nem megy át

C

-n, egy

C

-n átmenő kör²,
b) minden kör képe, amelyik nem megy át

C

-n, újra kör, amelyik nem megy át

C

-n.
a) Várható, hogy az állításban szereplő kör

C

-ből induló átmérőjének másik végpontja a

C

-ből az egyenesre bocsátott merőleges

T

talppontjának

S

inverz képe lesz (2. ábra).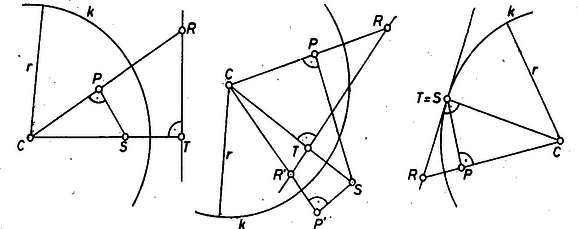

2. ábra

Megmutatjuk, hogy valóban az egyenes bármely,

T

-től különböző

R

pontjának

P

inverz képéből

C S

derékszögben látszik, tehát a

C S

átmérőjű körön van, és a kör minden,

C

-től különböző pontja az egyenes egy pontjának képe.
A

C P S

és

C T R

háromszögek a segédtétel szerint hasonlók, s mivel az előbbi

T

-nél derékszögű, így

C P S ∢ = 90^{\circ}

, amint állítottuk.
Megfordítva, ha

P

C S

átmérőjű kör tetszés szerinti,

C

-től különböző pontja, akkor,

R

-rel jelölve

C P

metszéspontját az egyenessel,

R

inverz képe egyrészt a

C R

félegyenesen van, másrészt a

C S

átmérőjű körön, tehát csak a

P

pont lehet.
A b) állítás bizonyításához is egy várható átmérőről mutatjuk meg, hogy az a kör minden pontjának a képéből derékszögben látszik. Ez a várható átmérő a

C

-től legtávolabbi

R_{1}

és a hozzá legközelebbi

R_{2}

pont

P_{1}

és

P_{2}

képét összekötő szakasz. Mind a négy pont egy egyenesen, az adott kör és

k

centrálisának az egyenesén van. Legyen az adott kör egy további pontja

R_{3}

, képe

P_{3}

(3. 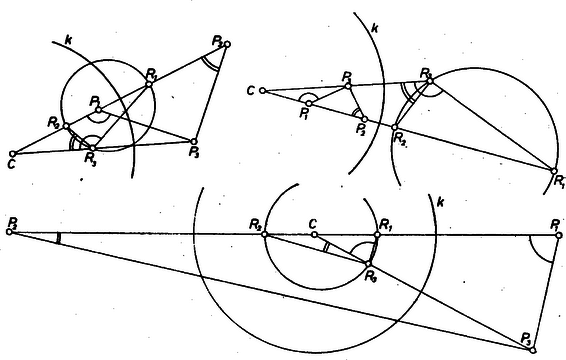ábra).

3. ábra

A segédtétel szerint a

C P_{1} P_{3}

és

C R_{3} R_{1}

, továbbá

C P_{2} P_{3}

és

C R_{3} R_{2}

háromszög hasonló, így

\begin{matrix} C P_{1} P_{3} ∢ = C R_{3} R_{1} ∢ és C P_{2} P_{3} ∢ = C R_{3} R_{2} ∢ . \end{matrix}

R_{1}

és

R_{2}

ugyanazon a

C

-ből induló félegyenesen van, akkor a bal oldali két szög a

P_{1} P_{2} P_{3}

háromszög

P_{1}

-nél levő külső szöge, ill.

P_{2}

-nél levő belső szöge, így

\begin{matrix} P_{1} P_{3} P_{2} ∢ = C P_{1} P_{3} ∢ - C P_{2} P_{3} ∢ = C R_{3} R_{1} ∢ - C R_{3} R_{2} ∢ = R_{2} R_{3} R_{1} ∢ = 90^{\circ}, \end{matrix}

mivel

R_{1} R_{2}

az adott kör egy átmérője.
Ha

R_{1}

és

R_{2}

között fekszik

C

, akkor egyszersmind

P_{1}

és

P_{2}

közt is fekszik, így a bal oldali szögek a

P_{1} P_{3} P_{2}

háromszög belső szögei, ezért

\begin{matrix} C P_{1} P_{3} ∢ + C P_{2} P_{3} ∢ = C R_{3} R_{1} ∢ + C R_{3} R_{2} ∢ = R_{1} R_{3} R_{2} ∢ = 90^{\circ}, \end{matrix}

P_{3}

tehát valóban a

P_{1} P_{2}

átmérőjű körön van.
Legyen most

P

ennek a körnek tetszés szerinti pontja. A

P C

egyenes vagy metszi az

R_{1} R_{2}

átmérőjű kört is, a

P_{1} P_{2}

átmérőjű kört is, vagy mind a kettőt érinti, hiszen minden az előbbivel közös pont képe az utóbbival közös pont, ez, vagy ezek egyike pedig (ha két ilyen pont van)

P

, tehát

P

valóban egy az adott körön levő pont képe.
Görbékre is fennáll, amit pontokra mondtunk, hogy ha egyikük egy másiknak a képe, akkor az utóbbi is az előbbinek a képe.
Az eddig belátottakat összefoglalhatjuk úgy, hogy az inverzió az egyenesekből és körökből álló halmazt önmagába viszi át, vagyis minden egyenest és kört egyenesbe vagy körbe visz át.
Az inverzió egy további hasznos tulajdonsága, hogy szögtartó. Természetesen ahhoz, hogy egy szög képéről mint egy újabb szögről beszélhessünk, értelmezni kell közös végpontú körívek szögét. Ezen a közös végpontban az ívekhez húzott érintő félegyenesek szögét értjük.
A szög ilyen értelmezése mellett egy szög és a képe egyenlő nagyságú. Legyen

R

egy tetszőleges pont, melyre

0 < C R \neq r

, és

e

egy tetszőleges,

R

-végpontú,

C

-n nem átmenő félegyenes. A

C R

szakasz

R

-en túli meghosszabbítása legyen a

g

félegyenes, végül az

R

pont inverzét jelöljük

P

-vel, a

P

R

pontokon átmenő,

e

-t érintő kört

k_{1}

-gyel. A

k_{1}

kör két pontban metszi

k

-t, hiszen

P

és

R

egyike

k

-nak belső pontja, a másik

k

-n kívül van,

k_{1}

inverze is átmegy e metszéspontokon és a

P

R

pontokon,

k_{1}

-nek tehát az inverzével

4

közös pontja van, így

k_{1}

-et az inverzió önmagába viszi át (4. ábra).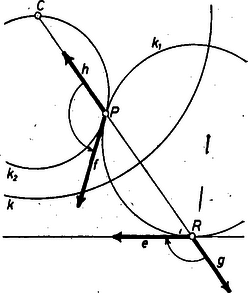

4. ábra

Legyen az

e

g

félegyeneseknek a

P R

szakasz felező merőlegesére vonatkozó tükörképe

f

h

. Ekkor a

g

e

félegyenesek szöge egyenlő nagyságú, és ellentétes irányú, mint a

h

f

félegyenesek szöge. Az

e

egyenesnek

k_{1}

-gyel csak egy közös pontja van,

R

, így

e

inverzének, a

k_{2}

körnek is csak egy közös pontja van vele,

k_{1}

és

k_{2}

tehát érintik egymást

P

-ben; emiatt

k_{1}

-nek

P

-beli érintője, az

f

félegyenes,

k_{2}

-t is érinti: az

e

g

félegyenesek szögét tehát az inverzió is az

f

h

félegyenesek szögébe viszi át, így állításunkat a speciálisan választott

e

g

szögre már bebizonyítottuk.
Ha az

R

pontból tetszőleges két félegyenes indul, mondjuk

e_{1}

és

e_{2}

, akkor az

e_{1}

-et

e_{2}

-be vivő forgatás előállítható az

e_{1}

-et

g

-be, majd a

g

-t

e_{2}

-be vivő forgatások egymás után való végrehajtásával, ez utóbbi két szög inverze a fentiek alapján velük egyenlő nagyságú, de ellentétes irányítású, ugyanez igaz tehát az összegükre is.
Végül megjegyezzük, hogy ha

R

k

körön van, akkor invertáljunk először a

C

középpontú,

r' < r

sugarú

k'

körre, majd a kapott képet

r^{2} : r'^{2}

arányban a

C

centrumból megnagyítva előállíthatjuk a

k

-ra vonatkozó inverzet. A

k'

-re való invertálás a fentiek alapján az

R

-csúcsú szögek irányítását ellentétesre változtatja, de e szögek nagyságát nem változtatja meg, a centrális hasonlóság a szögek nagyságát is, irányítását is megtartja, a

k

-ra való invertálás tehát ebben az esetben is megváltoztatja a szögek irányítását, de a nagyságukat változatlanul hagyja. Állításunk bizonyítását befejeztük.
Végül megmutatjuk, hogyan alkalmazhatók az elmondottak az 1542. feladat³ megoldására. E feladat első részében lényegében azt kellett megmutatnunk, hogy tetszőleges

A B C

háromszögben, melynek talpponti háromszöge

A' B' C'

, az

A

és

M

pontok harmonikusan választják el a

P

A'

pontokat, ahol

M

a magasságpont, és

P

A A'

B' C'

egyenesek metszéspontja. Ez a kifejezés azt jelenti, hogy

\begin{matrix} \frac{A P}{P M} : \frac{A A'}{A' M} = - 1, \end{matrix}

ha az egyes szakaszok hosszát előjelesen vesszük, vagyis az

A A'

egyenest tetszőlegesen irányítjuk, és az ezzel az irányítással megegyező irányítású szakaszok hosszát pozitívnak, az ellentétes irányításúakét pedig negatívnak tekintjük. (A mondott feladatban az irányítástól eltekintettünk.)
Először megmutatjuk, hogy tetszőleges

R

pont, melyre

0 < C R \neq r

, és az

R

inverze,

P

harmonikusan választja el

k

-nak az

R P

egyenesen levő

A

B

pontjait. Válasszuk az

R C

félegyenes irányát pozitívnak, és legyen

A

C R

félegyenesen, ekkor valóban

\begin{matrix} \frac{R A}{A P} : \frac{R B}{B P} = \frac{R C - r}{r - P C} : \frac{R C + r}{- r - P C} = - \frac{(R C - r) (P C + r)}{(r - P C) (r + R C)} = \\ - \frac{R C \cdot P C - r \cdot P C + r \cdot R C - r^{2}}{r^{2} - r \cdot P C + r \cdot R C - R C \cdot P C} = - 1. \end{matrix}

Invertáljuk az

A B C

háromszög

k_{1}

Feuerbach-körét az

A M

szakasz feletti

k

Thalész-körre. A

B'

C'

pontok mindkét körön rajta vannak,

k_{1}

átmegy az inverzió

O

centrumán,

k_{1}

inverze tehát a

B' C'

egyenes. Az

A'

pont inverzét az

O A'

egyenes metszi ki

B' C'

-ből,

A'

inverze tehát

P

, így feladatunk állítása előrebocsátott megjegyzésünkből következik.
Feladatunk második részében többek között a

k

kört határoztuk meg az

M

pont és

B C

B' C'

szakaszok

D

, ill.

D'

felezőpontja alapján. A fentiekből következik, hogy

D

-nek

k

-ra vonatkozó inverze

D'

. Feladatunknak ez a része tehát úgyis fogalmazható, hogy adott az inverzió alapkörének egyetlen pontja,

M

és egy további

D

pont,

D'

képével együtt. Legyenek a

D D'

egyenes

k

-val alkotott metszéspontjai

U

és

V

. Ekkor

D

D'

harmonikusan választja el az

U

V

pontokat. Emiatt a

D D'

feletti

k_{2}

Thalész-körre invertálva

U

-t, éppen a

V

pontot kapjuk,

k

-nak

k_{2}

-re vonatkozó inverze tehát önmaga. Az

M

pont

k_{2}

-re vonatkozó inverze legyen

M'

, ez is rajta van

k

-n. Tehát

k

középpontját az

M M'

szakasz felező merőlegese metszi ki a

D D'

egyenesből. Ha

M

D D'

szakasz felező merőlegesén van, akkor

M M'

felező merőlegese párhuzamos

D D'

-vel,

k

-nak

O

középpontja nem jön létre. Ebben az esetben az inverzió helyébe a

D D'

felező merőlegesére való tükrözés lép.

¹Lásd ezen számban, 136. o.

²Az említett feladatmegoldásban ez bizonyítva van $k$ -t metsző egyenesre.

³Lásd ezen számban, 102. o.