Kezdőlap


Cím:	Az 1169. gyakorlat megoldása vektorok segítségével
Szerző(k):	Tusnády Gábor
Füzet:	1968/október, 49 - 51. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vektorok segítségével az elemi matematika számolást igénylő feladatait is egyszerűen megoldhatjuk. Jól szemlélteti ezt a megállapítást az 1169. gyakorlat¹ alábbi megoldása.
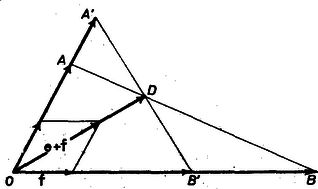
Legyen a harmonikus közép megszerkesztéséhez használt szög csúcsa $0$ , a szárakra felmért $a$ , $b$ szakaszok végpontja $A$ , ill. $B$ . Vegyünk fel az $0$ -ból $A$ -ba, ill. $B$ -be mutató egységvektorokat, legyenek ezek e, ill. f. E vektorok választása miatt az $a = \vec{O A}$ , $b = \vec{O B}$ vektorok előállíthatók $a = a e$ , $b = b f$ alakban, ahol $a$ , $b$ épp az $O A$ , $O B$ szakaszok előírt hossza. Mivel az e, f vektorok hossza egyenlő, a $g=e+f$ vektor szerkesztéséhez használt paralelogramma rombusz, g állása tehát megadja az $A O B$ szög felezőjének az állását. Messe az $A B$ egyenes ezt a szögfelezőt $D$ -ben, első lépésként a $d = \vec{O D}$ vektort állítjuk elő az e, f vektorok segítségével.

Mivel

D

rajta van az

A B

egyenesen,

\vec{O D} = \vec{O A} + λ \bar{A B}

, ahol

λ

alkalmasan választott skalár; azaz

\begin{matrix} d = a + λ ((b-a) = (1 - λ) a + λ b = (1 - λ) a e + λ b f . \end{matrix}

(1)

Mivel

D

a szögfelezőn is rajta van,

\vec{O D} = μ g

, ahol

μ

ugyancsak alkalmasan választott szám; azaz

\begin{matrix} d = μ g = μ (e + f) = μ e + μ f . \end{matrix}

(2)

A d vektorra tehát két előállítást is kaptunk, ezekben

λ

és

μ

ismeretlen. Meghatározásukhoz azt használjuk fel, hogy a d kívánt előállítása egyértelmű, tehát a kétfajta előállításban szereplő együtthatók rendre egyenlőek:

\begin{matrix} (1 - λ) a & = μ, & (3) \\ λ b & = μ . \end{matrix}

Ennek az egyenletrendszernek a megoldása adja

λ

μ

értékeit:

\begin{matrix} λ = \frac{a}{a + b}; μ = \frac{a b}{a + b} . \end{matrix}

(4)

A d vektor keresett előállítása tehát:

\begin{matrix} d = \frac{a b}{a + b} (e + f) . \end{matrix}

(5)

Szerkesztésünk következő lépésében az

O D

egyenesre a

D

pontban emelt merőlegessel metszettük a szög szárait. Legyenek a metszéspontok rendre az

A'

B'

pontok, ekkor

A

B

előállításához hasonlóan

a' = \vec{O A'} = h e

b' = \vec{O B'} = h f

, ahol

h

O A'

O B'

szakaszok hossza. Feladatunk a

h

meghatározása. Azt használjuk fel, hogy

D

A' B'

szakasz felezőpontja. Emiatt

\begin{matrix} d = \frac{1}{2} (a' + b') = \frac{h}{2} (e + f), \end{matrix}

(6)

így a d vektor egy újabb előállítását kaptuk, melynek meg kell egyeznie a korábbi, (5) alatti előállítással, tehát

\begin{matrix} h = \frac{2 a b}{a + b}, \end{matrix}

(7)

amint azt bizonyítanunk kellett.

Megoldásunkkal kapcsolatban megjegyezzük, hogy az (1) alatti összefüggés alapján

\vec{A D} = λ (b - a)

\vec{D B} = (1 - λ) (b - a)

, az

\vec{A D}

\vec{D B}

vektorok hossza tehát úgy aránylik egymáshoz, mint

λ : (1 - λ)

. Ebből (4) alapján kapjuk, hogy

\begin{matrix} A D : D B = \frac{a}{a + b} : \frac{b}{a + b} = a' : b, \end{matrix}

(8)

tehát a szögfelezőre vonatkozó ismert tételnek is egy újabb levezetését kaptuk. Ezt a tételt felhasználva az (5) alatti előállítást egyszerűbben is megkaphattuk volna a következő segédtétel alapján:

O

pontból az

A B

egyenes egy tetszőleges

C

pontjába mutató

c = \bar{O C}

vektor előállítható

\begin{matrix} c = \frac{α a + β b}{α + β} \end{matrix}

(9)

alakban, ahol

\begin{matrix} α : β = A C : C B \end{matrix}

(10)

(ez utóbbi arányban az

A C

C B

szakaszok hosszát előjelesen értjük: ha

A C

C B

iránya megegyezik, akkor előjelük egyforma, ha

A C

C B

ellentétes irányú, akkor a két szakasz hossza ellentétes előjelű).
Valóban, a c vektor által meghatározott

C

pontra

\begin{matrix} \vec{A C} = c - a = \frac{α a + β b}{α + β} - a = \frac{β}{α + β} (b - a) = \frac{β}{α + β} \vec{A B}, \end{matrix}

tehát

\vec{A C}

és

\vec{A B}

állása megegyezik, így

C

A B

egyenesen van. Hasonló módon kapjuk, hogy

\begin{matrix} \vec{C B} = \frac{α}{α + β} \vec{A B}, \end{matrix}

tehát a (9) alatti vektor által meghatározott

C

pontra érvényes (10).
Megoldásunk alapján az

A B O

háromszög szögfelezőjének a hosszát is kiszámíthatjuk. A

g = e + f

vektor szerkesztése alapján

\begin{matrix} | g | = 2 cos \frac{ω}{2}, \end{matrix}

ahol

ω = A O B ∢

. Így (5) alapján

\begin{matrix} O D = \frac{2 a b}{a + b} cos \frac{ω}{2} . \end{matrix}

¹Lásd ezen számban 70. o.