Cím: 1967. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1968/május, 193 - 202. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Egy egész számokból álló halmaz tartalmazza minden elemének kétszeresét és bármely két elemének összegét. A halmaz elemei között van pozitív és negatív is. Bizonyítsuk be, hogy a halmaz bármely két elemének különbsége a halmazhoz tartozik.

 
A feladat egy elem kétszereséről és két elem összegéről szól. Szólhatott volna ehelyett két nem feltétlenül különböző elem összegéről, megoldásaink azonban az eredeti szöveghez igazodnak.
 
I. megoldás. Először azt bizonyítjuk be, hogy ha c a halmaznak egy eleme és n természetes szám, akkor nc is a halmazhoz tartozik. Ezt n-re vonatkozó teljes indukcióval végezzük. Minthogy maga c és a feladat feltevése szerint 2c is a halmazhoz tartozik, elég belátnunk, hagy ha n>1 és nc a halmazban van, akkor (n+1)c is a halmaz eleme. Ez a feladat feltevéséből valóban következik, hiszen (n+1)c=nc+c, tehát a halmaz két elemének összegével egyenlő.
Legyen a>0 a halmaz legkisebb pozitív eleme, b<0 pedig a halmaz legnagyobb (azaz legkisebb abszolút értékű) negatív eleme. Minthogy a+b a halmazhoz tartozik, és rá
b<a+b<a,
viszont sem a-nál kisebb pozitív, sem b-nél nagyobb negatív szám nem lehet, azért csak 0-val lehet egyenlő. Eszerint 0 a halmaz eleme és b=-a. Ebből következik, hogy a minden egész számú többszöröse a halmazhoz tartozik, hiszen ez az na, 0, nb számok mindegyikére igaz, akármekkora is az n természetes szám.
Azt állítjuk, hogy a egész számú többszörösein kívül nincs a halmaznak más eleme. Tegyük fel ezzel ellentétben, hogy van a halmazban olyan x elem, amely a két szomszédos egész számú többszöröse, qa és (q+1)a között van. Ez az elem
x=qa+r(0<r<a)
alakban volna írható. Ebből azonban az következnék, hogy
r=x+(-q)a
is a halmazhoz tartozik, hiszen a halmaz két elemének összege. Ez azonban 0<r<a miatt ellentmond a megválasztásának, s így állításunk helyességét igazolja.
A feladat állításának helyessége most már következik abból, hogy a két egész számú többszörösének különbsége a-nak ugyancsak egész számú többszöröse.
 
II. megoldás. Felhasználjuk az első megoldás első bekezdésének eredményét. Bebizonyítjuk, hogy ha a a halmaz eleme, akkor -a is a halmazhoz tartozik.
Feltehetjük, hogy a≠0. Legyen b a halmaznak egy a-val ellentétes előjelű eleme. Eszerint
|b|a+|a|b=0,-a=[|b|-1]a+|a|b.


Ha |b|=1, akkor a jobboldal első tagja 0. Eszerint -a vagy b természetes számszorosa, vagy a és b természetes számszorosának összege, tehát mindenképpen a halmaz eleme.
Eszerint a halmaz két elemének különbsége, azaz egy elemének és egy másik elem (-1)-szeresének összege szintén a halmazhoz tartozik.
 
Megjegyzés. Második megoldásunkból csekély módosítással következik, hogy a feladat állítása akkor is helyes, ha benne egész számokból álló halmaz helyett racionális számokból álló halmazról van szó.
Ehhez csak azt kell meggondolnunk, hogy az első megoldás első bekezdése változatlanul helytálló marad, s hogy az ellentétes előjelű a, b racionális számokhoz találhatók olyan m, n természetes számok, amelyekre ma+nb=0. Ebből ugyanúgy következtethetünk tovább, ahogyan a második megoldásban tettük.
 
Második feladat. Egy konvex sokszöget egymást nem metsző átlók háromszögekre bontanak fel. A sokszög minden csúcsa páratlan sok ilyen háromszög csúcsa. Bizonyítsuk be, hogy a sokszög oldalszáma 3-mal osztható.
 
A feladatban konvex sokszög szerepel, de ez a megszorítás nyilván lényegtelen, a következőkben nem is támaszkodunk rá. Ilyen megszorítás nélkül azonban zavarhatná a megoldót az a kérdés, vajon felbontható-e minden sokszög egymást nem metsző átlókkal háromszögekre. Ez így van, de ennek bizonyítása nem könnyű.
Lényegtelenül módosul a feladat, ha egymást nem metsző átlókkal való felbontás helyett az n-szöget olyan háromszöghalmaz egyesítéseként állítjuk elő, amelyben minden háromszög minden csúcsa az n-szög csúcsai közül való, s amelyben nincs két egymásra boruló háromszög. Ez az átszövegezés csak annyit változtat, hogy így a feladat az n=3 esetben sem veszti értelmét, mert a háromszöghalmaz egyetlen elemből, magából a háromszögből is állhat. Eszerint ebben az esetben a feladat követelése és állítása is teljesül.
 
I. megoldás. Minden a felbontásban szereplő átló a sokszöget két sokszögre vágja fel. Tekintsük az így keletkező részsokszögek oldalszámának minimumát. Azt állítjuk, hogy ez a minimum 3, hogy tehát szerepel olyan átló, amely sokszögünkből háromszöget vág le. Ha ugyanis a minimum k>3 volna és pl. az A1Ak átló által levágott A1A2...Ak-1Ak sokszög valósítaná meg, akkor kellene, hogy e k-szög egy AiAj átlója is szerepeljen a felbontásban, hiszen háromszögekre való felbontásról van szó. Mivel az AiAj átló által levágott AiAi+1...Aj sokszög oldalszáma k-nál kisebb, k valóban nem lehet minimum.
A vizsgált részsokszögek között van 3-nál nagyobb oldalszámú is, mert különben egy átló a sokszöget két háromszögre bontaná fel, s ennek végpontjaiban a feladat követelésével ellentétben 2 háromszög találkoznék.
A vizsgált részsokszögek között nincs négyszög, mert ezt egy a felbontásban szereplő átlónak két háromszögre kellene felbontania, és így ennek az átlónak egyik végpontjában 2 háromszög találkoznék.
Ezek szerint a vizsgált részsokszögek oldalszámai között van 3-nál nagyobb, s ezek között a 3-nál nagyobb oldalszámok közül a legkisebbnek az értéke legalább 5. Legyen pl. az A1Ak átló által levágott A1A2...Ak-1Ak ilyen legkisebb oldalszámú, de háromszögtől különböző részsokszög. Beláttuk már, hogy 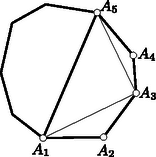k≥5.
 
 

1. ábra
 

Minthogy a felbontás a most említett részsokszöget is háromszögekre bontja fel, felbontásában egy A1AiAk, háromszög is fellép. k minimum-tulajdonsága miatt sem A1Ai, sem AiAk nem vághat le 3-nál nagyobb oldalszámú (és természetesen k-nál kisebb oldalszámú) sokszöget, ezért i≤3 és k-i+1≤3. Ezek az egyenlőtlenségek a fenti k≥5 eredménnyel együtt
0≤k-5≤i-3≤0
alakban írhatók, s innen k=5 és i=3 adódik.
Ezzel beláttuk, hogy sokszögünk felbontásában fellép olyan átló, amely ötszöget vág le, s hogy ezt az ötszöget a felbontó átlók három olyan háromszögre vágják fel, amelyek közül az ötszöget levágó átló végpontjaiban kettő-kettő találkozik (1. ábra). Hagyjuk el eredeti sokszögünkből ezt az ötszöget. Ezáltal a sokszög oldalszáma 3-mal csökken, a megmaradó sokszög átlókkal való felbontása viszont változatlanul eleget tesz a feladat követelményének, hiszen az egy csúcsba futó háromszögek száma csak két csúcsnál ad új értéket, s ott 2-vel csökkent.
Eszerint eljárásunkat a kapott sokszögre újból alkalmazhatjuk, ezt folytatva a sokszög oldalszámát minden lépésben 3-mal csökkenthetjük mindaddig, amíg a maradó sokszögben még van átló, amíg tehát háromszöghöz nem jutunk. Ezért az eredeti sokszög oldalszáma valóban osztható 3-mal.
Megoldásunkból az is kiolvasható, hogy ha n osztható 3-mal, akkor a konvex n-szög felbontható a feladat követelményét kielégítő módon.
 
II. megoldás. A bizonyítást n-re vonatkozó teljes indukcióval végezzük el. A feladat szövege után említettek szerint az állítás az n=3 esetben helyes. Elegendő tehát azt bizonyítanunk, hogy ha a feladat állítása egy n>3 értéknél kisebb oldalszámú sokszögekre helyes, akkor n-szögekre is helyes.
Ezt a bizonyítást egy megjegyzéssel készítjük elő. Azt állítjuk, hogy ha egy sokszöget egymást nem metsző átlókkal háromszögekre bontunk fel, és a sokszög csúcsairól egynek kivételével tudjuk, hogy az páratlan sok háromszögnek a csúcsa, akkor ez minden csúcsra igaz. Ennek igazolása végett arra hivatkozunk, hogy minden átlónak két vége van, tehát az átlóvégek száma páros. Minthogy a kivételes csúcstól eltekintve minden csúcsról tudjuk, hogy páratlan sok háromszög ér oda, tehát ott páros sok (esetleg 0) átlóvég helyezkedik el, a kivételes csúcsra is páros sok átlóvég marad, s így az is páratlan sok háromszög csúcsa.
A teljes indukciós bizonyításra térve tekintsünk egy a feladat követelményét kielégítő módon felbontott, n>3 oldalú sokszöget, s ennek egy a felbontásában fellépő AB átlóját. Minthogy az A csúcsban ettől az átlótól eltekintve páratlan sok átló vége helyezkedik el, az AB átló egyik oldalán ezeknek az átlóvégeknek a száma páros. Ezen az oldalon az AB átló n-szögünkből egy S1 sokszöget vág le. Az n-szög felbontása S1-et is háromszögekre bontja fel. Erről a felbontásról megállapíthatjuk, hogy minden B-től különböző csúcsnál páros sok átlóvég helyezkedik el. Az előre bocsátott megjegyzés szerint tehát ez B-re is teljesül, azaz S1 felbontása eleget tesz a feladat követelményének.
Az AB átlóihoz az S1-gyel átellenes oldalon a felbontás egy ABC háromszöge támaszkodik (2. ábra).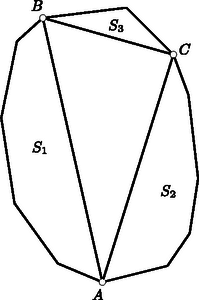
 
 

2. ábra
 

E háromszög AC, BC oldalai a háromszöggel átellenes oldalon n-szögünkből az S2 és S3 sokszöget vágják le. Az n-szöget eszerint az ABC háromszögre és az S1, S2, S3 sokszögekre bontottuk fel.
Minthogy az n-szöget felbontó átlók A-nál elhelyezkedő végei közül S1 belsejében páros sok van és kettő az ABC háromszög oldalának vége, S2 belsejében is páros sok helyezkedik el. Ugyanezt a B csúcsról és az S3-ban elhelyezkedő átlóvégekről is elmondhatjuk. Az előre bocsátott megjegyzés szerint tehát S2 és S3 felbontása is eleget tesz a feladat követelményének.
Mivel S1, S2 és S3 oldalszáma n-nél kisebb, indukciós feltevésünk szerint mindegyiknek az oldalszáma osztható 3-mal. Ezeknek az oldalszámoknak az összege azonban n+3, hiszen az ABC háromszög oldalai lépnek fel többletként. Így tehát n is osztható 3-mal.
 
III. megoldás. Először bebizonyítjuk, mégpedig teljes indukcióval, hogy egy sokszög egymást nem metsző átlókkal háromszögekre való felbontásakor a háromszögek két színnel kiszínezhetők úgy, hogy egyszínű háromszögeknek ne legyen közös oldala. Ez egyetlen háromszögre semmitmondóan igaz. Legyen tehát n>3, és tegyük fel, hogy az állítás n-nél kisebb oldalszámú sokszögekre igaz. Az egyik átló az n-szöget két sokszögre vágja fel. Minthogy ezek oldalszáma n-nél kisebb, indukciós feltevésünk szerint mindkettő a kívánt módon kiszínezhető a két színnel. Az egyikben a színeket esetleg felcserélve azt is elérhetjük, hogy a kettévágó átlóhoz a két sokszögben más-más színű háromszög támaszkodjék. Ilyen módon az n-szögnek a követelményünket kielégítő kiszínezéséhez jutottunk el.
Ha az n-szög felbontása eleget tesz feladatunk követelményének, akkor a háromszögek említett kiszínezésekor az n-szög oldalaihoz mindenütt ugyanolyan színű háromszög támaszkodik. Ezt elegendő két szomszédos oldalra belátnunk, s ezekre abból következik, hogy találkozási pontjukba páratlan sok háromszög ér el, s mivel ezek felváltva más-más színűek, a két szélső, tehát a sokszög említett két oldalára támaszkodó, ugyanolyan színű. A 3. ábra ilyen színezést mutat be.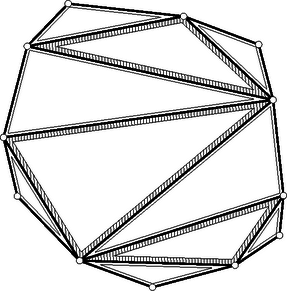
 

 

3. ábra
 

Az egyik színt a világos, a másikat a sötét keretezés szemlélteti. Ábránkban a sokszög határára mindenütt világos keretű háromszög támaszkodik.
Ha v világos és s sötét keretű háromszög szerepel, akkor ezeknek összesen 3v világosan és 3s sőtéten keretezett oldaluk van. Legyen a sokszög minden oldala világosan keretezett. Átlói két oldalról más-más keretet kaptak. Ezért a világosan keretezett oldalak számából a sötéten keretezettekét levonva a sokszög oldalszámát kapjuk meg:
n=3v-3s,
n tehát valóban 3-mal osztható.
 

Megjegyzések. 1. Második megoldásunk mintájára könnyű bebizonyítani a feladat állításának következő általánosítását: Egy konvex sokszöget egymást nem metsző átlók k-szögekre bontanak fel. A konvex sokszög minden csúcsa páratlan sok ilyen k-szög csúcsa. A sokszög oldalszáma ekkor
k[1+m(k-2)]
alakú, ahol m természetes szám. A bizonyítást az olvasóra hagyjuk.
2. Ugyancsak feladatként említjük meg Gallai Tibornak azt az eredményét, amely harmadik megoldásunk mintájára könnyen igazolható, s amely a következőképpen szól: Ha egy konvex sokszöget egymást nem metsző átlókkal háromszögekre bontunk fel, akkor az a páros sok csúcs, amelyben páros sok háromszög találkozik, a sokszög határvonalát töröttvonalakra bontja fel. Ha e töröttvonalak oldalszámait sorra váltakozó előjelekkel ellátva összeadjuk, 3-mal osztható eredményhez jutunk.
 
 

4. ábra
 

A 4. ábra sokszögénél a szóban forgó csúcsokat körökkel jelöltük meg. Ha a legalsó ilyen csúcstól pozitív forgásirányban haladunk, akkor váltakozó előjelekkel képzett összegként 6-2+1-2 adódik, ami valóban 3-mal osztható. Eredeti feladatunk a most közölt eredménynek azt a határesetét tartalmazza, amikor 0 azoknak a csúcsoknak a száma, ahol páros sok háromszög találkozik.
 
Harmadik feladat. Bizonyítsuk be, hogy a konvex négyszögek közül csak a parallelogrammáknak van meg az a tulajdonságuk, hogy mind a négy csúcs esetében ugyanakkora összeget kapunk, ha a csúcsnak a rajta át nem haladó oldalegyenesektől való távolságait összeadjuk.
 
I. megoldás. Segédtételként fel fogjuk használni, hogy egy konvex szögtartomány két pontjának a száregyenesektől való távolságait összeadva akkor és csak akkor kapunk ugyanakkora összeget, ha a két pont összekötő egyenese a szögfelezőre merőleges.
Tekintsük ennek bizonyítása végett az AOB konvex szögtartományban elhelyezkedő P pontot. Messe a P pontból a szögfelezőre bocsátott merőleges a szárakat az A, B pontokban (5. ábra).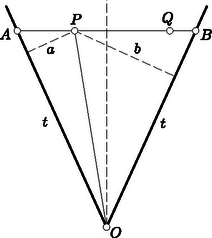
 
 

5. ábra
 

Legyen OA=OB=t és a P pontnak az OA, OB egyenesektől való távolsága a és b. Minthogy az AOBΔ területe az AOPΔ és BOPΔ területének összege, e terület kétszerese at+bt=(a+b)t. Eszerint a
(P,AOB∢)=a+b
távolságösszeg az AB szakasz minden pontjára ugyanakkora, és akkora, mint az A pont távolsága az OB egyenestől. Minthogy azonban az OA szár minden pontja az OB egyenestől más-más távolságra van, a P és Q pontok akkor és csak akkor adnak ugyanakkora távolságösszeget, ha belőlük a szögfelezőre merőlegest bocsátva az OA szárnak ugyanahhoz a pontjához jutunk, ha tehát a PQ egyenes a szögfelezőre merőleges.
A bizonyításra térve feltesszük, hogy a feladat követelménye a konvex ABCD négyszögre teljesül. A bizonyítást kisérő 6. ábra szándékosan torz, hiszen éppen azt kell bizonyítanunk, hogy csak paralelogramma adhatja a helyes ábrát, és ilyen ábra annak felhasználására csábítana, amit bizonyítani akarunk.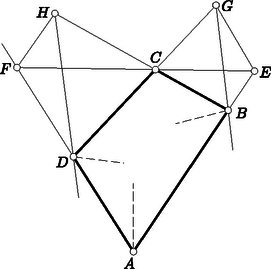
 
 

6. ábra
 

A C ponton át a BAD∢ felezőjére merőlegest bocsátunk. Messe ez az AB, AD szárakat az E, F pontokban. Az E ponton át AD-vel párhuzamost húzunk, s ez a DC egyenest G-ben metszi. Hasonlóan legyen H a BC egyenes és az F-en át AB-vel húzott párhuzamos metszéspontja. A CBEΔ és CHFΔ, valamint ugyanígy a CGEΔ és CDFΔ hasonló, mert oldalaik páronként egy egyenesen vannak, illetőleg párhuzamosak. Ebből következik, hogy a CBEG és CHFD négyszögek is hasonlók, hogy ezért CBG∢=CHD∢, hogy tehát a BG és DH egyenesek párhuzamosak.
Segédtételünk szerint (C,DAB∢)=(E,DAB∢), a párhuzamosság miatt (E,DAB∢)=(G,ADC∢), a feladat feltevése szerint pedig (C,DAB∢)=(B,ADC∢). Ezekből (G,ADC∢)=(B,ADC∢) következik, tehát segédtételünk szerint az is, hogy a GB egyenes az ADC∢ felezőjére merőleges. Ugyanígy következik, hogy HD merőleges az ABC∢ felezőjére. Minthogy azonban a most említett egyenesek párhuzamosak, az ABC∢ és ADC∢ felezői is párhuzamosak. Ha tehát a DCB∢-et egy ezekkel a szögfelezőkkel párhuzamos egyenesre tükrözzük, szárai a DAB∢ száraival párhuzamos helyzetbe jutnak. Ezért e szögek egyenlők, azaz az ABCD négyszögben A-nál és C-nél egyenlő szögek vannak. Ugyanígy adódik, hogy a négyszög másik két szemközti szöge is egyenlő, tehát a négyszög paralelogramma.
A paralelogrammának valóban megvan a feladatban leírt tulajdonsága, mert bármely csúcsból indulunk is ki, mindig a két magasság összegéhez jutunk. (Ez a megoldás Pogáts Ferenctől és Herczeg Jánostól való.)
 
II. megoldás. Felhasználjuk azt, hogy ha egy konvex φ szög egyik szárára a csúcstól felmérjük a t távolságot, a végpont a másik szár egyenesétől tsinφ távolságra van.
A négyszög betűzését úgy választjuk meg, hogy az AB és DC félegyenesek és ugyanígy a CB és DA félegyenesek messék egymást vagy párhuzamosak legyenek (7. ábra).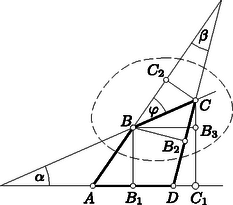
 

 

7. ábra
 

Legyen β és α e félegyenespárok hajlásszöge, párhuzamosság esetén tehát α=0 és β=0 is lehetséges. Legyen továbbá ABC∢=π-φ s így BCD∢=β+φ.
Jelölje C1 és C2 a C pont vetületét az AD, AB egyeneseken, B1, B2 és B3 pedig a B pont vetületét az AD, CD és CC1 egyeneseken. Ha a feladat követelménye a B és C csúcsokra teljesül, akkor
CC1+CC2=BB1+BB2.
Minthogy CC1-BB1=CB3,
CB3+CC2=BB2,
amit e megoldás első bekezdése alapján
BCsinα+BCsin(π-φ)=BCsin(β+φ)
alakban írhatunk, hiszen az itt fellépő távolságokhoz úgy jutunk, hogy a CBB3∢=α,ABC∢=π-φ és BCD∢=β+φ szög egyik szárára felmérjük a BC szakaszt, s a kapott végpontnak a másik szár egyenesétől való távolságát tekintjük.
Utolsó egyenletünkből BC-vel osztva
sinα+sinφ=sinβcosφ+cosβsinφ
adódik. Ehhez hasonlóan, a feladat követelményének az A, B csúcsokra való teljesülésére építve azt kapjuk, hogy
sinβ+sinφ=sinαcosφ+cosαsinφ.
Utolsó két egyenletünket összeadva
(sinα+sinβ)(1-cosφ)+(2-cosα-cosβ)sinφ=0.
Itt 0<φ<π miatt mindkét tag második tényezője pozitív, első tényezőik viszont nem-negatívak. Az egyenlőség tehát csak úgy állhat fenn, ha
sinα+sinβ=0,cosα+cosβ=2.
Mivel 0≤α<π és 0≤β<π, mindkét eredményünkből α=β=0 következik, ami éppen azt jelenti, hogy az ABCD négyszög parallelogramma.
 
Megjegyzés. Ez a megoldás valamivel egyszerűbbé válik, ha a jelölést úgy választjuk meg, hogy sinα≥sinβ is teljesüljön. Ekkor elég az előző bekezdés alsó egyenletére építenünk, mert ez
(sinα-sinβ)+sinβ(1-cosφ)+(1-cosβ)sinφ=0
alakban írható. Itt egyik tag sem lehet negatív, és összegük 1-cosφ és sinφ pozitivitása miatt csak akkor lehet 0, ha
sinα=sinβ,sinβ=0,cosβ=1,
amiből α=β=0 következik.
 
III. megoldás. Abból a megállapításból indulunk ki, hogy ha egy négyszög eleget tesz a feladat követelményének, akkor az olyan másik négyszög is eleget tesz, amelynek oldalai az első négyszög oldalaival rendre párhuzamosak. Ez közvetlenül kiolvasható abból, hogy második megoldásunk a követelmény teljesülését szögek közötti összefüggésekkel fejezte ki. Nem kell azonban ehhez szögfüggvényekre sem hivatkoznunk. Elegendő annak megállapítása, hogy a 7. ábra szaggatott vonallal körülkerített részét a BC szakasz és a négy oldalirány már meghatározza. Ha tehát egy rendre párhuzamos oldalakkal bíró másik négyszögből indulunk ki, az előbbihez hasonló ábrarészhez jutunk. Eszerint a feladat követelményének a B, C pontokra való teljesülését biztosító CB3+CC2=BB2 összefüggés megfelelője a másik négyszögre is teljesül. Ezért ez a négyszög is kielégíti a feladat követelményét, hiszen a B, C csúcsok szerepét itt bármely két csúcs átveheti.
A feladat követélményét kielégítő négyszög egyik oldalegyenesét párhuzamosan eltolva elérhetjük, hogy az új konvex ABCD négyszög két szomszédos oldala egyenlő legyen, pl. AB=CB (8. 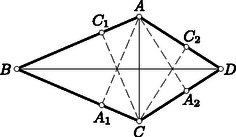ábra).
 
 

8. ábra
 

Jelölje A1, A2 és C1, C2 az A és C pont vetületét a CB, CD és AB, AD egyeneseken. Minthogy fenti megállapításunk szerint a feladat követelménye az új négyszögre is teljesül,
AA1+AA2=CC1+CC2,
tehát az ABCΔ egyenlő szárúságából következő AA1=CC1 miatt
AA2=CC2.
Ezért a derékszögű ACA2Δ és CAC2Δ egybevágó, s így ACA2∢=CAC2∢. Az ABCΔ alapján nyugvó szögek egyenlőségét is figyelembe véve azt kapjuk, hogy az új négyszögben A-nál és C-nél elhelyezkedő szögek egyenlők, s ezért ez az eredeti négyszög megfelelő szögeire is áll. Ugyanígy adódik a másik két szemközti szög egyenlősége, tehát az is, hogy paralelogrammáról van szó. (Ez a megoldás Böröczki Károlytól való.)
 
IV. megoldás. A feladat mit sem változik, ha benne nem a csúcsnak a rajta át nem haladó oldalegyenesektől való távolságait adjuk össze, hanem mind a négy oldalegyenestől való távolság összegéről szólunk, hiszen a csúcson áthaladó oldalegyenestől való távolság 0. A feladatot most ebben az alakban tekintjük, és megoldásához a vektorokra vonatkozó alapismereteket is felhasználunk.
Legyen n egy félsík határegyenesére merőleges, a félsík belseje felé mutató egységvektor. Legyen A és B a félsík két pontja, a és b pedig e pontok távolsága a határegyenestől (9. ábra).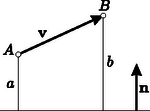
 

9. ábra
 

Felhasználjuk, hogy e távolságok különbsége, azaz az A-ból B-be vezető v vektor n-nel párhuzamos összetevőjének előjeles hossza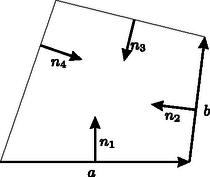
b-a=vn.
Legyenek n1, n2, n3, n4 a feladat követelményeit kielégítő négyszög oldalaira merőleges, a négyszög belseje felé mutató egységvektorok, továbbá a és b a négyszög két egymáshoz csatlakozó oldalvektora (10. ábra).
 

10. ábra
 

Minthogy 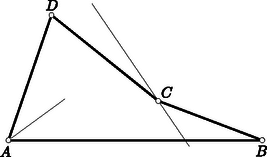a két végpontjára a négy oldalegyenestől való távolság összege ugyanakkora, e két összeg különbsége, azaz a megfelelő távolságok különbségeinek összege 0. A fentiek szerint tehát
an1+an2+an3+an4=a (n1+n2+n3+n4)=0.
A b vektorra ugyanígy
b (n1+n2+n3+n4)=0
adódik. Eszerint n1+n2+n3+n4 merőleges az egymással nem párhuzamos a, b vektorok mindegyikére, ami csak úgy lehetséges, ha
n1+n2+n3+n4=0.
Ha tehát e négy vektort egymáshoz fűzzük, zárt négyszöget kapunk. E négyszög mindegyik oldala egységnyi, tehát rombusz és szemközti oldalai párhuzamosak. Ezért az eredeti négyszög rájuk merőleges szemközti oldalai is párhuzamosak, és e négyszög valóban paralelogramma.
 
Megjegyzések. 1. A feladat konvex négyszögről szólt. Megmutatjuk, hogy ez a megszorítás felesleges, mert konkáv négyszögre a feladat követelménye nem teljesülhet. Legyen az ABCD négyszögben a C csúcsnál konkáv szög. A C csúcson át a DAB∢ felezőjére merőlegest állítunk. Ez a négyszögnek legalább egy csúcsát, pl. a B csúcsot elválasztja az A csúcstól (11. ábra), hiszen a konkáv szög nem helyezkedhetik el a merőleges egyenesnek egy oldalán.
 

 

11. ábra
 

Ezért az első megoldás segédtétele szerint az ott használt jelöléssel (C,DAB∢)<(B,DAB∢). Minthogy itt a jobboldalon a B pontnak az AD egyenestől való távolsága áll, s ez kisebb, mint a B pontnak az AD, CD egyenesektől való távolságainak összege, a feladat követelménye a B és C csúcsokra valóban nem teljesülhet.
A feladat követelése konkáv négyszögekre akkor sem teljesülhet, ha az oldalegyenesektől való távolságokat előjellel látjuk el, negatívnak mondva a távolságot, ha a pont az oldalegyenesnek a másik oldalán van, mint amerről a négyszög az oldalra támaszkodik. Negyedik megoldásunk ezt is bebizonyítja.
2. A második és negyedik megoldás mutatja, hagy a feladat állításának helyességét már az is biztosítja, ha csak három csúcsra követeljük meg a távolságösszegek egyenlőségét. Ha ez az összeg három csúcsra egyenlő, akkor eszerint a negyedik csúcsra is ugyanakkora.
A legutóbbi mondat megállapítása messzemenően általánosítható. Negyedik megoldásunk mintájára könnyen belátható, hogy ha a síkban véges sok egyenest adunk meg, mindegyiknél megszabva, hogy melyik oldalán elhelyezkedő pontokra mondjuk a pontnak az egyenestől való távolságát pozitívnak és melyikre negatívnak, ha továbbá a sík három nem egy egyenesen levő pontjára az egyenesektől való távolságok összege ugyanakkora, akkor a sík minden pontja ugyanekkora távolságösszeget ad. Ez többek között azt is jelenti, hogy ha egy konvex n-szög esetében három csúcsra az oldalegyenesektől való távolságok összege ugyanakkora, akkor ugyanekkora minden csúcsra, sőt az n-szög minden pontjára is. A negyedik megoldás alapján könnyen belátható, hogy egy konvex n-szögnek akkor van meg a most említett tulajdonsága, ha oldalai egy egységoldalú konvex n-szög oldalaira rendre merőlegesek.