Cím: Egy számelrendezés szomszédos számpárjainak különbségeiről. Megjegyzések az 1147. gyakorlathoz
Szerző(k):  Bakos Tibor ,  Nemetz Tibor ,  Tusnády Gábor 
Füzet: 1968/május, 202 - 204. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek
Hivatkozás(ok):Feladatok: 1967/október: 1147. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzések az 1147. gyakorlathoz1

 

Gondoljuk, hogy előttünk fekszik az 1‐18 egész számok összes lehetséges elrendezése az 1147. gyakorlat úthálózatának pontjain, továbbá hogy minden egyes elrendezés mellett fel van tüntetve a szomszédos számpárjai közti különbségek legkisebbike, d, valamint legnagyobbikuk, D. Kérdezzük, mi a talált összes d értékek legnagyobbika, d*, és mi a talált D értékek legkisebbike: D*.
Bebizonyítjuk, hogy mindkét keresett érték 6-tal egyenlő, mégpedig úgy, hogy egyrészt külön-külön belátjuk a d*<7, illetőleg D*>5 egyenlőtlenséget, másrészt példát adunk olyan elrendezésre, melyben d=6, illetőleg D=6. Az előbbire már az 1147. gyakorlat megoldása tartalmaz példákat, az utóbbira példa az 1. ábra.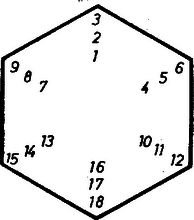
 

 

1. ábra
 

I. Tegyük fel, hogy van olyan X elrendezés, melyben egyetlen különbség sem kisebb 7-nél: d≥7. Egy ilyen elrendezésben egy n számmal szomszédos pontokon nem állhatnak az n-6-tól n+6-ig terjedő egész számok. Nem minden n esetében tartozik a kizárt 13 szám mindegyike az elrendezendő számok közé, azonban az a=8,9,10 és 11 számok mindegyike valóban legalább 13 számot zár ki, és legföljebb 5 számot enged meg szomszédjaként. Először ezek helyzetével foglalkozunk, ezeket B típusú számoknak nevezzük, a náluk kisebbeket A-, a nagyobbakat pedig C-típusúaknak.
Állítjuk, hogy bármelyik B-típusú számtól mindegyik másik B-számhoz a hálózat páros számú útszakaszát tartalmazó útvonalon jutunk át. Szemléletesebben mondhatjuk ki ezt annak az észrevételnek a felhasználásával, hogy a csomópontok kiszínezhetők két színnel úgy, hogy minden útszakasz két végpontja különböző színű.2 Állításunk ekkor azt mondja, hogy az X elrendezésben mind a négy B-szám ugyanolyan színű ponton áll, hiszen páros számú útszakaszból álló, nem zárt útvonal végpontjai megegyező színű pontok. (A 2. ábra a) és b) része azt mutatja, hogy a kis körút, ill. a középső körút 0 jelű pontjából kiindulva 1,2,..., útszakasz megtételével mely ponthoz érünk el; egy a nagy körúton kijelölt csomópontból való kiindulás megfelelő ábrája úgy adódik a-ból, hogy felcseréljük a sugárutak végpontjainak adatait.)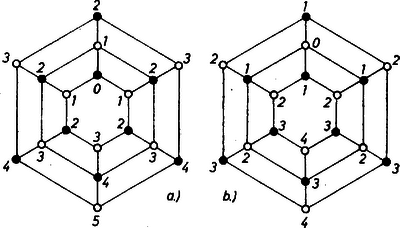
 

 

2. ábra
 

Amennyiben vegyesen világos és sötét ponton állnak a B-számok, eloszlásuk a két színre vagy 2:2 vagy 3:1. Ezek kizárása végett gondoljunk a B-számokkal szomszédos pontok betöltésére. Két ugyanolyan színű pontnak együttvéve legalább 5 szomszédja van ‐ hiszen egy pont 4, ill. 3 másikkal szomszédos aszerint, hogy a középső vagy valamelyik szélső körút megy át rajta ‐, továbbá közös szomszédaik száma legföljebb 2, ti. amikor pontosan az egyik a középső körúton áll. Így 2:2 eloszlás esetén a négy B-számnak együttvéve legalább 10 szomszédja lenne. Másrészt az A-típusú számok közül az a legnagyobb, ami még felléphet legalább egy B-szám mellett, a 11-7=4, a C-típusú számok közül pedig a legkisebb ilyen a 8+7=15. Így B-szám szomszédjaként szóba sem jöhet más szám, mint az 1, 2, 3, 4 (A0-típus) és 15, 16, 17, 18 (C0-típus). Ennyi pedig kevés a mondott 10 pont betöltéséhez.
Hasonlóan a 3:1 eloszlás esetén a három egyszínű pontnak együttvéve legalább 6 szomszédja van, a másik színűnek legalább 3, együtt ismét több, mint ahány A0- és C0-típusú szám van.
Ezek alapján mondhatjuk, hogy mindegyik B-szám pl. világos ponton áll. Megmutatjuk, hogy a 9 sötét pont nem tölthető be a d≥7 követelmény megtartásával. A sötét pontokban nyilván vegyesen állnak A- és C-típusú számok, valamelyik típus mindenesetre többségben van, hiszen a pontok száma páratlan. Mondhatjuk, hogy pl. C-szám van több (ugyanis minden számunk helyére az őt 19-re kiegészítő számot írva újra megfelelő elrendezést kapunk, és abban minden egyes A-, B-, C-típusú szám helyén rendre egy C-, B-, A-típusú szám áll), így a sötét ponton álló A-számok száma legföljebb 4.
Tekintsük e számok második szomszédait (amelyek persze szintén sötét ponton állnak). Minden pont legalább 5 másikkal áll másod-szomszédságban (2. ábrák), ezért minden sötét ponton álló A-számnak van legalább két C-típusú másodszomszédja. Különbségük legalább 14, mert közös szomszédjuk csak az A-típusúnál nagyobb és a C-típusúnál kisebb szám lehet; ezért csak A0-típusú szám szerepelhet sötét ponton, de közülük a 4-es sem, mert az ezt legalább 14-gyel meghaladó számok közül csak egy szerepelhet, a 18-as.
Emiatt legfeljebb három A0-típusú szám állhat sötét ponton, s legalább három C-típusú, náluk legalább 14-gyel nagyobb másodszomszédjuk van, így pedig a 3-as sem léphet fel. Ugyanígy a 2-es, végül az 1-es sem, így valóban nem tölthető be a 9 sötét pont, hiszen C-típusú szám csak 7 van, és valóban nem lehetséges X elrendezés.
II. Egy olyan Y elrendezésben, melyben D≤5, az 1, 2, 17, 18 számok egyike sem állhat a középső körúton. Ehhez belátjuk, hogy az 1, 18, az 1, 17, a 2, 18 és a 2, 17 számpárok egyikének tagjai sem állhatnak egymástól 4 útszakasznyinál kisebb távolságban. Az első három párban a különbség legalább 16, viszont 3 útszakaszon a legnagyobb megengedett különbséggel is ‐ mondjuk így: feszítetten is ‐ csak 3⋅5=15 különbség alakulhat ki. 2 és 17 pedig azért nem állhat 3 útszakasznyi távolságban, mert bármely pontból bármely olyan másikba, amely tőle 3 útszakasznyira van, mindig vezet két, közös közbülső pontot nem tartalmazó útvonal (2. ábrák), és nem állhat mindkét útvonal mentén a feszített 2, 7, 12, 17 számsorozat.
Mármost a középső körút pontjaitól csak 2‐2 másik pont van legalább 4 útszakasznyi távolságra, és ennyi az alábbiak szerint kevés a mondott 4 szám elrendezésére. Ha pl. az 1-es számot a 3. ábra B pontjába írjuk be ‐ jelképesen 1=B ‐, akkor 17 és 18 számára csak a K, M pontok jönnek szóba, így pedig a 2-es szintén csak B-ben állhatna, mert K-tól C, B, F és T vannak legalább 4 útszakasznyira, M-től pedig A, B, D és R, és e két felsorolásban csak B közös. Hasonlóan adódik állításunka 2-es, 17-es és 18-as s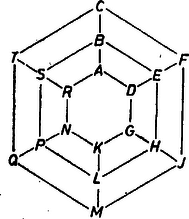zámra.
 

 

3. ábra
 

Ezek szerint, az ábra betöltését az 1-essel kezdve, lényegében csak 1=A jön szóba, és ekkor 17 és 18 számára J, M és Q közül kettő választandó. A J, Q pár nem választható, mert az előbbiekhez hasonlóan 2=A-ra vezet; az M, Q párból egyértelműen 2=D, az M, J pár pedig mellőzhető, mert tükörképe az utóbbinak a CM tengelyre nézve.
A 2, 17 számpárra fent mondottak érvényesek az 1, 16 párra is, ezért a 16-os csak L-ben vagy J-ben állhat. Folytassuk az 1=A, 2=D, 16=J elhelyezést. A H‐D különbség nem lehet feszítetten 2⋅5=10, azaz H≠12, mert D-ből H-ba E-n át is, G-n át is eljuthatunk, s nem lehet E=G=7. Így H-D≤9, és J-D=14 miatt J-H=5, azaz H=11, továbbá az E, G pontokba csak 6 és 7 irható. Ugyanígy J-E≤9 miatt E-D=5, ezért E=7, így pedig G=6, végül F=12.
A 2=D, 16=L kiindulás hasonlóan adja egymás után egyértelműen a H=11, G=7, E=6, E=12 elhelyezést. Mindig érvényes, hogy ha az n és n+14 számok távolsága 3 útszakasz, akkor a 14 egységnyi növekedés a köztük vezető két, közös közbülső pont nélküli útvonal egyikén az n, n+4, n+9, n+14 számokon megy végbe, másikukon pedig az n, n+5, n+10, n+14 számokon át, mert az egyetlen még gondolható n, n+5, n+9, n+14 sorozat amazok mindegyikét lehetetlenné, teszi. (A fenti két példán kívül a két végpont úgy is állhatna még egymáshoz képest, mint pl. A és K.)
Most már könnyen adódik, hogy a 3-as szám nem helyezhető el. Ugyanis egyrészt a 3, 18 pár távolsága is legalább 4 útszakasz, másrészt az iméntiek szerint a 3, 17 távolság is legalább 4. Ha ugyanis 3 és 17 távolsága 3, akkor a köztük levő két útvonal egyikén 3, 7, 12, 17 áll, holott a 12-est vagy F-be, vagy K-ba írtuk, és ezek egyike sem szomszédos sem M-mel, sem Q-val, ahol a 17-es állhat. Mármost M-től és Q-tól legalább 4 útszakasznyira A, B, D, R, ill. D, A, E, G van, tehát a 3-as részére csak a foglalt A és D felelne meg.
1Lásd ezen számban, 215. o.

2Lényegében véve ezt használta ki az 1147. gyakorlatban látott a) és b) elrendezés, a számokat,,kicsikre'' és,,nagyokra'' kettéosztva.