Cím: Munkadiagramok
Szerző(k):  Wehner, R. 
Füzet: 1967/április, 177 - 181. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fizikai fogalmakat, törvényeket megfogalmazni és megérteni általában kétféle módon lehet: vagy a betűszámtan vagy a geometria nyelvén. Az elsővel képletbe tömörítjük a különböző fizikai mennyiségek közötti összefüggéseket, míg a másodikkal grafikonokban, diagramokban tesszük szemléletessé a fizikai mennyiségek kapcsolatait. Mind a két módszerre szükség van. Az elsőt az elvontabb gondolkodásúak használják inkább az elméleti vizsgálódásnál, míg a diagramok módszere inkább a fizika technikai vonatkozásainál játszik nagy szerepet.
Középfokú fizikai tanulmányoknál mindkettőre szükség van. Kell az elvontabb képlet, de szükséges a szemléletes diagram is. Gondoljunk csak rá, milyen segítséget nyújt az erővel való számolásnál, ha azt irányított egyenes darabbal (vektorral) ábrázoljuk, vagy mennyire megkönnyíti a váltakozó áramok tulajdonságainak megértését a sinus-görbével való ábrázolás.
A következőkben egyetlen fizikai mennyiség, a munka grafikus ábrázolásán, diagramján keresztül szeretnénk bemutatni a fizika különböző területeiről vett példákon, hogyan lehet szemléletes módon eredményt elérni olyan esetekben is, amikor a képletekkel dolgozó módszer esetleg magasabb matematikai ismeretet tételez fel.
A következők figyelmes áttanulmányozása talán azt is eredményezni fogja, hogy észrevesszük, miszerint a munka és energia nagysága nemcsak erő és út szorzatából határozható meg, hanem ugyanehhez vezet a teljesítmény és idő, a nyomás és térfogat, elektromos töltés és feszültség, áramerősség, feszültség és idő szorzata is. Így a munka fogalmának átfogóbb megértéséhez is eljutunk.

 


Mechanika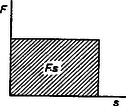
 

 
 
1. ábra
 

Az elmozdulás irányában ható, állandó erő munkájának diagramja könnyen elkészíthető, hiszen ha a derékszögű koordinátarendszer ordinátájára felmérjük alkalmas mértékben az erőt (F), az abszcisszára pedig az utat (s), akkor nyilván a munkát (W) az F⋅s nagyságú téglalap területe adja (l. 1. ábra). Ábrázoljuk most a csigákkal kapcsolatos következő feladatot. Egy G=600p súlyú terhet h=10cm magasba akarunk felemelni állócsigával, majd mozgó csigával, 4-tagú és végül 6-tagú csigasorral.
A kísérletek tanúsága szerint a szükséges felvonó erő és az általa megtett út (felhasznált fonalhossz) rendre a következő:
 

Álló csigánál: F=G;  s=h;
mozgó csigánál: F=G/2; s=2h;
4 -tagú csigasornál: F=G/4; s=4h;
6-tagú csigasornál: F=G/6, s=6h.
 


Ha ezt felrajzoljuk grafikonokban, látjuk, hogy a végzett munka minden esetben ugyanakkora (2. ábra).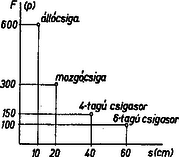
 
 
2. ábra
 

Lehetséges kombináltabb feladat is. A munkadiagram ilyenkor még inkább segít. Tekintsük a következő feladatot.
Egy kőműves n darab kisméretű téglából, melyek súlya egyenként ΔG, falat rak oly módon, hogy azokat egymásra helyezi. Mekkora munkát végez H magasságú fal elkészítése közben?
 
 
3. ábra
 

Nyilván a magasság, melyet minden tégla felemelésénél el kell érni, h=0-tól h=H-ig növekszik. Ennek megfelelően az egyes téglák felemelésével járó munka W=ΔG⋅0-tól W=ΔG⋅H értékig nő. Vigyük fel most e részmunkákat egy munkadiagramra (3. ábra). Így keskeny derékszögű csíkok összegeként jelentkező lépcsőzetes vonallal határolt ,,háromszög'' -idomot kapunk, melynek területe W≈G⋅H/2, ahol G az egész fal súlya, ami sok tégla esetén jóval nagyobb, mint az egyes téglák súlya, s így a közelítés is jó. A kapott eredményünk azonos azzal, mintha az egész G súlyú falat a súlypont H/2 magasságáig emeltük volna (4. ábra).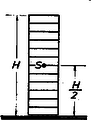
 
 
4. ábra
 

Lehetséges az is, hogy az erő a munkavégzés közben nem marad állandó. Példa erre a megnyújtott spirálrugó esete. A kísérletek szerint a nyújtó erő (F) mindig arányos a rugó megnyúlásával (s), vagyis F=k⋅s. Tehát az erő grafikonja egy, az origón átmenő egyenes, melynek irányszögét a k együttható határozza meg.
Ha F erő s megnyúlást hoz létre, akkor az általa végzett munka az erőt ábrázoló egyenes alatti háromszög területe (5. ábra), vagyis W=F⋅s/2, vagy, mivel F=k⋅s, azért W=k⋅s2/2.
Észrevehetjük, hogy ekkora a potenciális energia is, mely a megnyúlt rugóban munkavégzésre készenlétben áll; sőt az is látható, hogy minél kisebb a k értéke, vagyis minél lágyabb a rugó, annál kisebb munkára van szükség ugyanakkora megnyújtás létrehozásához.
 


Hőtan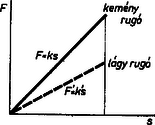
 
A hőtanban különös jelentőségük van a munkadiagramoknak a gőzgépek és robbanómotorok munkavégzésének és teljesítményének vizsgálatával és kiszámításával kapcsolatban.
 
 
5. ábra
 

Nézzük például a teljes nyomású, sűrítő nélküli gőzgép munkadiagramját. A q keresztmetszetű hengerben mozgó dugattyúra p nyomású gőz hat és elmozdítja s lökethosszon. Mivel a mozgató erő F=p⋅q, azért a gőz által végzett munka W=F⋅s=p⋅q⋅s=p⋅V, ahol V a lökettérfogat: Ha V-t literben, p-t at-ban mérjük, a W-t 10kpm-ben kapjuk.
Ha figyelembe vesszük, hogy a dugattyúra kívülről p1=1at nyomás hat, akkor a hasznos munka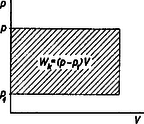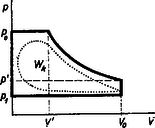
Wh=(p-p1)⋅V.
A diagram tehát az ábrán látható téglalap területe (6. ábra). Ha tudjuk, hogy egy másodpercben mennyi a dugattyú löketszáma, akkor kiszámítható a gőzgép teljesítménye.
 
 
6. ábra
 
 
7. ábra
 

Expanziós gőzgépeknél csak bizonyos lökettérfogatig (V') áramlik a p nyomású gőz a hengerbe, s azután jó közelítésben a Boyle-Mariotte törvény szerint kitágul, és nyomása leesik egy bizonyos p' értékre, majd kiáramlik. A munkadiagram tehát, figyelembe véve a külső nyomást is, a 7. ábrán látható. (p'-t az említett törvény segítségével állapíthatjuk meg, mert hiszen p'⋅V0=p0⋅V'.)
A görbe által körülzárt terület nagysága adja meg tehát a gőz munkáját egy löket alatt. Természetesen eltekintettünk minden veszteségtől. Így az ideális munkát kaptuk. A valóságban a munka kisebb ennél. (A pontozott vonal által körülzárt terület.) A reális diagramot egy szerkezet, az indikátor segítségével maga a gőzgép rajzolja fel, s a terület kiszámítását integráló gépek végzik. Az így kapott munka az ún. indikált munka.
 


Elektromosságtan
 
Hogy váltakozó áramok esetén a különböző típusú ellenállások (ohmos, induktív, kapacitív) jelenlétekor az áram munkadiagramját hogyan kell felhasználni a hatásos, látszólagos és meddő teljesítmény megértetésére, azt a gimnáziumi tankönyv kimerítően tárgyalja, ezért mellőzzük. Két elektromosságtani példa azonban hozzásegíthet bennünket az elektrodinamikai térszemlélet megértéséhez, mely szerint az elektromos és mágneses energiát maga az elektromágneses tér hordozza.
Először keressük egy kondenzátor feltöltésével járó munkát. Nyilván a töltési folyamatnál a töltőáram munkája változik át az elektromos tér energiájává. Az is világos viszont, hogy a W munkát nem adja meg egyszerűen a W=Q⋅U0 egyenlet, melyben Q a folyamatosan felvitt összes töltés és U0 a kondenzátor végső feszültsége, hiszen a kondenzátor U feszültsége nem állandó a töltés folyamán, hanem 0-tól U0-ig nő.
Gondoljuk azonban, hogy a Q töltést olyan kis ΔQ adagokban visszük át a kondenzátorra, hogy az U feszültség az átmenet alatt állandónak legyen tekinthető. (Gyakorlatban is véghez vihető ez, ha igen kicsi golyó segítségével visszük át a töltést az egyik kondenzátorról a másikra.)
Az első ΔQ töltés felvitele nem igényel energiát, mert nincs még taszító erő. De minél több töltésadagot viszünk át a kondenzátorra, annál nagyobb lesz a feszültség és így a ΔQ átviteléhez szükséges ΔQ⋅U munka is. Az egyes részmunkák (Wn=ΔQ⋅U) a Q-U diagramon keskeny téglalapokként jelentkeznek, melyek együtt egy ,,lépcsőzetes'' háromszög területét adják, mint azt a falazási példában is láttuk (8. ábra).
 
 
8. ábra
 

Mivel tudjuk, hogy a kondenzátoron a mindenkori feszültség arányos a rajta levő töltéssel (U=k⋅Q), ahol k csak a kondenzátort jellemző állandó, mely a kapacitással k=1/C kapcsolatban van, azért a diagramból leolvasható a kondenzátornak Q töltéssel U0 feszültségre való feltöltésekor végzett munka:
W=Q⋅U0/2=C⋅U02/2.
Ez az az energia, mely a kondenzátor elektromos terében felhalmozódik és tárolódik, s mely a kisütéskor felhasználható.
A következő példa annak a mágneses energiának a kiszámítása, mely egy tekercsben raktározódik fel, amikor rajta áram fut keresztül.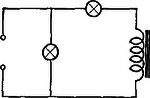
 
 
9. ábra
 

Ismeretes az a kísérlet, melyben egy vasmagos tekerccsel sorba kapcsolt izzólámpa később gyullad meg, mint egy, csak ohmos ellenállással sorba kapcsolt izzó (9. ábra). A második esetben a lámpán és az ellenálláson az elektromos energia azonnal meleggé és fénnyé alakul. Az elsőben ellenben az elektromos energia egy része előbb nyilván a tekercs mágneses terének felépítésére fordítódik. Egy sok menetes, zárt vasmagú (nagy L induktivitású) tekercsben erős mágneses tér épül fel, sok energia tárolódik s így kialakulása is hosszabban tart. A lámpa csak akkor gyullad fel, ha a tér már több energiát nem vesz fel. Ezután ebben a kapcsolásban is az áram munkája egészen hőenergiává változik. A mágneses tér fenntartásához nem szükséges energia. Ha az áram a tekercsben megszakad, a mágneses tér nem maradhat fenn, összeomlik. Energiája ismét elektromos energiává alakul. A tér igen rövid idő alatt eltűnik, miközben a tekercsben igen nagy feszültség lép fel. Az energiamegmaradás elve természetesen érvényben marad: amennyi energiát felvett a tér kialakulásakor, annyit fog visszaadni a megszűntekor. A tekercs is elektromos energiatároló, mint a kondenzátor, de nem sztatikus, hanem dinamikus.
A tárolt energia nagysága is kiszámítható a munkadiagram segítségével.
Ismeretes, hogy az L induktivitású tekercsben az önindukciós áram feszültsége
UL=-L⋅ΔIΔt,
ahol ΔI a Δt időre eső áramerősség-változás.
Növekvő áramerősségnél a tekercsben jelentkező indukált feszültség ellentétes a tekercsre kapcsolt U feszültséggel. Így a tekercsáram nagysága, ha R az ohmos ellenállás,
I=U-L⋅ΔIΔtR.

A következőkben az áramforrás által Δt idő alatt leadott U⋅I⋅Δt energiára lesz szükségünk. Megkapjuk ezt, ha az előbbi egyenletet I⋅Δt-vel szorozzuk és rendezzük: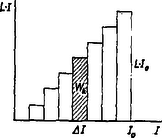
U⋅I⋅Δt=R⋅I2⋅Δt+I⋅LΔI.
Ez egy energiamérleg. Balról a betáplált energia (az áramforrás áramának munkája), mely jobbról két alakban jelenik meg. Az első nyilván a Δt idő alatt keletkezett hő, a másik a keresett energia, mely a tekercs mágneses terének létrehozásához szükséges. Az I⋅L⋅ΔI tag nyilván akkor nem zérus, ha ΔI≠0, vagyis míg az áramerősség változik.
 
 
10. ábra
 

A teljes mágneses térenergiát akkor kapjuk meg, ha összegezzük az egyes Δt időszakok alatt a mágneses tér részére leadott energiaértékeket. Tudjuk, hogy I⋅L⋅ΔI munka-jellegű, tehát összege munkadiagram, mely keskeny téglalap alakú sávokból tevődik össze (10. ábra). A diagram ismét ,,lépcsőzetes'' háromszög, s így a teljes tárolt energia
Wm=L⋅I02/2,
ahol I0 az áram állandó erőssége, mely az áramkörben a mágneses tér kialakulása után folyik.
Természetesen mindkét elektromosságtani példánkban, mivel áramok munkájáról van szó, mind a ΔQ, mind a ΔI tetszés szerinti kicsinynek vehető s így a kapott eredmény egészen pontos.
Természetesen a bemutatott példák csak igen egyszerűek voltak, a technikában sokkal bonyolultabb problémákkal lehet találkozni. De a gondolatmenet mindig ugyanez: elkészítjük a munkadiagramot és területméréssel megállapítjuk a munkát.
 
 Prof. Dr. R. Wehner, (Güstrow)