Első pillanatban talán meglepő, ha a sport fizikai alapjairól tesznek említést. A közhiedelem szerint csak a biológia áll szoros kapcsolatban a sportmozgásokkal. A nagy sportteljesítmények mögött biológiai vonatkozásokat sejtünk. A sportélettan szerepe a teljesítmények fokozása területén tagadhatatlan ugyan, de előtérbe kerülnek azok a fizikai alapokon nyugvó elméleti és kísérleti módszerek is, amelyek segítségével a további fejlődés biztosítható.
Tekintsük át a mechanika azon fejezeteit, ahol viszonylag egyszerű számítással nyomon tudjuk követni, magyarázni tudjuk a sport kialakult vagy fejlődésben levő módszereit.

x=v02g⋅sin2α;x akkor maximális, ha $\text{sin}2\alpha =1;$ $\alpha ={45}^{\circ }$.
A sportban előforduló hajítások (dobások, ugrások) az előbbinél általánosabbak, mert a test (sportszer) indítása és érkezése nem egy szinten történik.
Jelöljük $T$-vel a becsapódás vízszintes síkja és az indítási pont közti távolságot (1. ábra) és ebben az általános esetben határozzuk meg a vízszintes elmozdulást.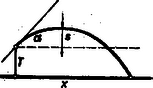

 

 

1. ábra

 

Az emelkedés ideje

$\begin{array}{c}{\displaystyle t_1=\frac{v_0\text{sin}\alpha }{g}\mathrm{,}}\end{array}$

az emelkedés

$\begin{array}{c}{\displaystyle s_1=\frac{v_0^2\text{sin}{}^2\alpha }{2g}\mathrm{.}}\end{array}$

Az esés

$\begin{array}{c}{\displaystyle s_2=s_1+T=\frac{g}{2}{t}_2^2\mathrm{,}}\end{array}$

amiből helyettesítés és átrendezés után

$\begin{array}{c}{\displaystyle t_2=\frac{\sqrt[]{v_0^2\text{sin}{}^2\alpha +2gT}}{g}\mathrm{.}}\end{array}$

Mivel $x=v_0\text{cos}\alpha \cdot \left(t_1+t_2\right)$, helyettesítés után

$\begin{array}{c}{\displaystyle x=v_0\text{cos}\alpha \cdot \left(\frac{v_0\text{sin}\alpha }{g}+\frac{\sqrt[]{v_0^2\text{sin}{}^2\alpha +2gT}}{g}\right)}\end{array}$

($1\text{'}$)

adódik.
Algebrai és trigonometriai átalakítások után

$\begin{array}{c}{\displaystyle x=\frac{v_0^2}{2g}\left(\text{sin}2\alpha +\sqrt[]{\text{sin}{}^{2}2\alpha +\frac{8gT\text{cos}{}^2\alpha }{v}}\right)}\end{array}$

(1)

összefüggéshez jutunk. ($T=0$ esetén az ismert $x=\frac{v_0^2}{g}\text{sin}2\alpha$ alakot kapjuk.)
Ezek után megvizsgálhatjuk a kérdést, hogy befolyásolhatja-e és ha igen, hogyan befolyásolja a dobás távolságát az indítás magassága?
Az I. sz. táblázat a súlylökés, ill. kalapácsvetés távolságának $T$-től, az indítás magasságától való függését mutatja be: súlylökésnél $12\text{m/s}$, kalapácsvetésnél $25\text{m/s}$ kezdősebesség mellett ($\alpha ={45}^{\circ }\mathrm{,}g=9\mathrm{,}8{\text{m/s}}^2$).

$\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\multicolumn{3}{c}{{\displaystyle \text{<span style="font-style: italic;">I. sz. táblázat</span>}}}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>T</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math> <span style="font-weight: normal;font-style: normal;">(súlylökés; m)</span> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math> <span style="font-weight: normal;font-style: normal;">(kalapácsvetés; m)</span> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mn>,</mn><mn>9</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>16</mn><mn>,</mn><mn>40</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>65</mn><mn>,</mn><mn>62</mn></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>1</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>16</mn><mn>,</mn><mn>58</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>65</mn><mn>,</mn><mn>79</mn></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>3</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>16</mn><mn>,</mn><mn>72</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>65</mn><mn>,</mn><mn>99</mn></math> }}\hfill \end{array}}}\end{array}$

A magasabb(ról) dobó tehát tekintélyes mértékben előnyben van alacsonyabb társával szemben!
Már említettük, hogy ferde hajítás esetén $\alpha ={45}^{\circ }$-os szög esetén jut a test legmesszebbre. Kérdés, hogy $T$ magasságról indítva is ${45}^{\circ }$-e az optimális szög?
Az (1) összefüggés alapján számolva nehézkesen tudnánk azt a szöget meghatározni, amely mellett az $x$ maximális. Egyszerűbb úton kapunk választ kérdésünkre, ha azon összefüggések alapján számolunk, amelyek Vermes Miklós: ,,A burkológörbékről'' c. cikkében találhatók.^{${}^{*}$}
Ezek: $y=\left(-T\right)=F-\frac{1}{4F}{x}^2$ és $\text{tg}\alpha =\frac{2F}{x}\left(\text{ahol}F=\frac{v_0^2}{2g}\right)$.
Fenti összefüggések a maximális távolságot $\left(x\right)$ és az optimális szöget $\left(\alpha \right)$ szolgáltatják.
Számítással könnyen meggyőződhetünk arról, hogy $v_0=12\text{m/s}\mathrm{,}$ $T=2\mathrm{,}3\text{m}$ esetén $x_{\text{max}}=16\mathrm{,}84\text{m}$, ha $\alpha =41\mathrm{,}{1}^{\circ }$, míg változatlan $T$, de $v_0=25\text{m/s}$ esetén $x_{\text{max}}=66\mathrm{,}03\text{m}$, ha $\alpha ={44}^{\circ }\left(g=9\mathrm{,}8\text{m/s}\right)$.
A ${45}^{\circ }$-tól való szögeltérés jelentős ($3\mathrm{,}{9}^{\circ }$, ill. $1^{\circ }$), a távolságnövekedés az előbbi táblázat (I. sz.) alapján 12 cm, ill. 4 cm, versenyeken a sportoló helyezését erősen befolyásoló tényező lehet!
A nagyobb magasságról való indítás, mint láttuk, előnyös a dobásoknál, kérdés, előnyös-e, ha a sportoló tömege nagyobb?
Ezt a kérdést vizsgáljuk meg annak a gerelyhajítónak az esetében, aki úgy dob, hogy
a) lábait szilárdan rögzíti a földön a dobás pillanatában,
b) a dobás pillanatában mindkét lábával elhagyja a földet, felugrik, hogy ,,ne törje meg'' a dobás lendületét.
Legyen mindkét esetben $T=2\mathrm{,}31\text{m}$, $g=9\mathrm{,}8{\text{m/s}}^2$, $\alpha ={45}^{\circ }$ (utóbbi az egyszerűbb számítás kedvéért; a valóságban ‐ anatómiai okokból ‐ gerelyhajításnál ${40}^{\circ }$‐${42}^{\circ }$ a kidobás szöge), akkor
$a)$ $v_0=26\text{m/s}$ esetén $x=71\mathrm{,}20\mathrm{,}\text{m}$,
$b)$ ha a felugrás pillanatában a gerelyhajító sebessége $8\text{m/s}$ és a gerely sebességét ezután fokozza karjának ugyanakkora erőkifejtésével, mint $a)$ esetben, akkor a földhöz viszonyított kidobási sebesség a mozgásmennyiség megmaradásának törvénye értelmében kisebb lesz, mint $a)$ esetben.
Legyen az össztömeg $m=80\text{kg}$, a gerely tömege $m\text{'}=0\mathrm{,}8\text{kg}$ és $v_1$ a hátralökődés sebessége:

$\begin{array}{c}{\displaystyle m\text{'}\left(26-8\right)\text{m/s}=\left(m-m\text{'}\right)\cdot v_1\mathrm{,}}\end{array}$

$\begin{array}{c}{\displaystyle v{\text{'}}_0=26-v_1\text{alapján}}\end{array}$

$\begin{array}{c}{\displaystyle v{\text{'}}_0=25\mathrm{,}82\text{m/s}\mathrm{,}x\text{'}=70\mathrm{,}23\text{m}\mathrm{.}}\end{array}$

A csökkenés (97 cm) jelentős. Természetesen, ha a sportoló tömege nagyobb lenne, mint példánkban, a dobási sebesség és távolság sem csökkenne ekkora mértékben! Ha tehát a sportoló felugrik dobás közben, kevésbé hátrányos, ha nagyobb a tömege.
Helytelen tehát, mert károsan befolyásolja a sporteredményt, ha a sportoló felugrik dobás közben. Ha szilárdan megveti a lábát a földön, nem csökken a kidobás sebessége. Kidobás közben azonban (különösen súlylökésnél) elkerülhetetlen a törzs bizonyos mértékű káros mozgása még ebben az esetben is, így némi előnyt jelent (kevésbé hátrányos), ha nagyobb a sportoló tömege.
Milyen fizikai tényezők befolyásolhatják még a dobás eredményét? Mivel a felsorolásuk is hosszadalmas lenne, ragadjunk ki néhány olyat közülük, ahol befolyásoló voltuk számítással könnyen igazolható.
Az atlétikai versenyszabályok szerint a dobópálya 1:1000 arányban lejthet. Ez, egy várhatóan $66\text{m}$ hosszú dobásnál $6\mathrm{,}6\text{cm}$ ,,süllyedést'' jelent. $g=9\mathrm{,}8{\text{m/s}}^2$, $\alpha ={45}^{\circ }$, $v_0=25\text{m/s}$ és $T=\left(2\mathrm{,}3+0\mathrm{,}065\right)\text{m}$ mellett $x=66\mathrm{,}04\text{m}$.
Az I. sz. táblázattal összehasonlítva kitűnik, hogy a szabály adta lehetőség 5 cm növekedést jelenthet. Ez a versenyszabály tehát előnyt jelenthet csúcseredmények hitelesítésénél.
Előnytelen viszont a dobószámoknál az, hogy a dobásoknak (a gerelyhajítás kivételével) adott átmérőjű (súlylökésnél $2\mathrm{,}13\text{m}$) körből kell történnie. Ezzel korlátozott a gyorsítás útja $\left(s\right)$ és ezzel a kidobás sebessége $\left(v\right)$ adott gyorsító erő mellett.
P. O'Brien amerikai súlylökő ,,sportújítása'' az volt, hogy háttal állt a kidobás irányának s így a gyorsítás útját $s$-ről $s\text{'}$-re növelte meg. Ha a ható erőt a kidobás folyamán állandónak tételezzük fel, az egyenletesen változó mozgás törvényeinek felhasználásával

$\begin{array}{c}{\displaystyle s=\frac{v^2}{2a}\text{és}s\text{'}=\frac{v{\text{'}}^2}{2a}\text{alapján}v{\text{'}}^2=v^2\frac{s\text{'}}{s}\mathrm{.}}\end{array}$

Alkalmazzuk most nyert összefüggésünket arra az esetre, amikor $s=2\mathrm{,}1\text{m}$, $s\text{'}=2\mathrm{,}4\text{m}$, $v=12\text{m/s}\mathrm{,}$ $\alpha ={45}^{\circ }$, $T=2\mathrm{,}3\text{m}$. Az I. sz. táblázat alapján $x=16\mathrm{,}72\text{m}$, míg (1) alapján számolva $x\text{'}=18\mathrm{,}85\text{m}$; az újítás ebben az esetben $2\mathrm{,}13\text{m}$ többletet jelent!
Ismeretes, hogy a Föld különböző pontjain más-más a nehézségi gyorsulás értéke.
A 0. szélességi fokon (Egyenlítő)$g=9\mathrm{,}78{\text{m/s}}^2\mathrm{,}$
a 60. szélességi fokon   $g=9\mathrm{,}82{\text{m/s}}^2$.

$\alpha ={45}^{\circ }$, $T=2\mathrm{,}3\text{m}$, $v_0=25\text{m/s}$ mellett (kalapácsvetés) $x_{0\left(B\right)}=66\mathrm{,}12\text{m}$, $x_{60.}=65\mathrm{,}86\text{m}$.
A $g$ értékének ilyen változása tehát $26\text{cm}$-t jelent. Ez azt jelenti, hogy kedvező pályalejtés és földrajzi fekvés (Egyenlítő) esetében $26\text{cm}+5\text{cm}=31\text{cm}$ növekedés adódhat azonos képesség mellett! Ez elgondolkoztató és egyszer talán azt eredményezi, hogy a csúcseredményeket is éppúgy ,,redukálják'', mint pl. a barométerállást.
A magasság nemcsak a dobásoknál előnyös, hanem a labdajátékoknál is. Ezek közül a teniszjáték adogatását emeljük ki. A 2. ábra a teniszpálya alakját és méreteit mutatja. Az ún, adogatás úgy történhet, hogy az adogató játékos az 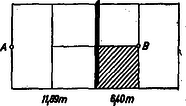$A$ pontról a labdát a $0\mathrm{,}915\text{m}$ magas háló fölött ellenfele térfelének bevonalkázott részére juttatja. Az egyszerűbb számítás miatt csak azokat az adogatásokat vesszük figyelembe, melyeknél a labda az $AB$ egyenesszakasz megfelelő pontjaira jut. Lényegében így is ugyanarra az eredményre jutunk, mint az általánosabb esetben.

 

 

2. ábra

 

Hasonlítsuk össze, hogy egy $2\mathrm{,}6$ és egy $2\mathrm{,}9\text{m}$ magasról ütő játékos közül melyik és milyen arányban van előnyösebb helyzetben?
A szakemberek (edzők és játékosok) szerint a ,,jó'' szög alatt indított, $v_0=30-40\text{m/s}$ sebességű adogatás szinte foghatatlan. (Nagyon nehéz szabályosan visszaütni.) Egy-egy teniszmérkőzés kimenetelét sokszor ezek az ún. ,,ász'' adogatások döntik el.
A számítások részletezése helyett inkább a gondolatmenetét adjuk meg. Az adott kezdősebesség mellett olyan szögben kell indítani a labdát, hogy
a) túljusson a hálón (felette haladjon),
b) a vízszintes elmozdulás $\left(x\right)$ ne legyen több, mint $AB$. (Megállapodtunk, hogy egyszerűség kedvéért csak ezeket az ütéseket tárgyaljuk.)
A számításokat a már említett ,,A burkológörbékről'' c. cikk

$\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{2F\pm \sqrt[]{4F^2-4Fy-x^2}}{x}}\end{array}$

összefüggése alapján végezhetjük el, ahol $\alpha$ a kérdéses szög,

$-y$ pedig

${\displaystyle \begin{array}{cc}\hfill {\displaystyle x}& {\displaystyle =18\mathrm{,}29\text{m}\text{esetén}2\mathrm{,}6\text{m}\mathrm{,}\text{ill.}2\mathrm{,}9\text{m}\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =11\mathrm{,}89\text{m}\text{esetén}2\mathrm{,}6\text{m}-0\mathrm{,}915\text{m}\text{ill.}}\hfill \end{array}}$

$2\mathrm{,}9\text{m}-0\mathrm{,}915\text{m}\left(-y=R\right)\mathrm{.}$
A számítás eredményét az alábbi, II. sz. táblázat tartalmazza.

$\phantom{111111}$ II. sz. táblázat

${\displaystyle \begin{array}{ccccc}\hfill {\displaystyle }\hfill & \multicolumn{2}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>v</mi></mrow><mrow><mn>0</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>30</mn></math> m/s}}}& \multicolumn{2}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>v</mi></mrow><mrow><mn>0</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>40</mn></math> m/s}}}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>T</mi></math>(m)}}\hfill & \multicolumn{1}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>6</mn></math>}}}& \multicolumn{1}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>9</mn></math>}}}& \multicolumn{1}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>6</mn></math>}}}& \multicolumn{1}{c}{{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>9</mn></math>}}}\\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn><mn>,</mn><mrow><msup><mrow><mn>41</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>3</mn><mn>,</mn><mrow><msup><mrow><mn>35</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn><mn>,</mn><mrow><msup><mrow><mn>00</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn><mn>,</mn><mrow><msup><mrow><mn>62</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>4</mn><mn>,</mn><mrow><msup><mrow><mn>38</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn><mn>,</mn><mrow><msup><mrow><mn>76</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn><mn>,</mn><mrow><msup><mrow><mn>76</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>7</mn><mn>,</mn><mrow><msup><mrow><mn>19</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}\\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mn>,</mn><mrow><msup><mrow><mn>97</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mrow><msup><mrow><mn>41</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mrow><msup><mrow><mn>76</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mn>,</mn><mrow><msup><mrow><mn>57</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math> }}\end{array}}$

$*$^{${}^{*}$}
Mit olvashatunk ki a táblázatból?
1. Ilyen nagy kezdősebességnél a szög negatív, a labda tehát indításának pillanatától kezdve közeledik a talajhoz.
2. A kezdősebesség növelésekor a szög abszolút értéke növekszik (pl. $2\mathrm{,}{41}^{\circ }$ és $5\mathrm{,}{00}^{\circ }$), a labda pályája egyre jobban megközelíti az egyenest.
3. A magasabbról ütő játékos előnyben van, mert nála nagyobb annak a két szögértéknek a különbsége, amelynél az adogatás még szabályos (pl. $2\mathrm{,}{41}^{\circ }$ az $1\mathrm{,}{97}^{\circ }$-kal szemben), ilyen módon valószínűbb, hogy jól adogat, mint alacsonyabbtól ütő társa (3. ábra).

 

 

3. ábra

 

4. A kezdősebesség növelése azt eredményezi, hogy csökken $|{\alpha }_1|$ és $|{\alpha }_2|$ különbsége, az adogatás végrehajtásánál tehát egyre erősebben kell koncentrálni.
Nem tartalmazza a táblázat a negatív ${\alpha }_1$, ${\alpha }_2$ pozitív megfelelőit. Ezek sportszempontból érdektelenek, ,,nincsenek értelmezve'', mert az igen meredek röppálya befutásához olyan tetemes idő szükséges, hogy azalatt az ellenfél jól fel tud készülni a labda védhetetlen visszaütéséhez.
Ugrásnál a versenyző súlypontja mozog parabola pályán. Távolugrásnál a nekifutás $\left(v_1\right)$ és az elrugaszkodás $\left(v_2\right)$ sebessége az, amire mérések alapján könnyebb következtetni (4. ábra). A szög is másodrendű kérdés.

 

 

4. ábra

 

A távolugró karja, lába bonyolult mozgást végez ugrás közben, a súlypontja azonban biztosan parabolapályát ír le. Mivel az elrugaszkodás közel nyújtott, a talajtérés behajlított lábakkal történik, itt is fellép egy $T$ szintkülönbség. Vegyük ezt számításainkban $1\text{m}-0\mathrm{,}5\text{m}=0\mathrm{,}5\text{m}$-nek.
Először azonban a vízszintes elmozdulást szeretnénk az új követelményeknek megfelelően meghatározni. Ha $\left(1\text{'}\right)$-ben

${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle v_0\cdot \text{cos}\alpha \text{helyére}{v}_1-\text{et}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle v_0\cdot \text{sin}\alpha \text{helyére}{v}_2-\text{t írunk}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle x=v_1\cdot \frac{v_2+\sqrt[]{v_2^2+2gT}}{g}}\hfill & \text{(<mn>2</mn>)}\end{array}}$

összefüggéshez jutunk, mely csak az ismert sebességértékeket tartalmazza, a szöget nem.
Alkalmazásakor ismét nem elégszünk meg csupán ugrások távolságának meghatározásával.
A tapasztalat azt mutatja, hogy a nekifutás sebességének fokozásával (ami az ugrás távolságát növeli) az elrugaszkodás sebessége csökken. (Ez viszont az ugrás távolságát csökkenti.) Ilyenformán lehetséges, hogy a nekifutás sebességét egy bizonyos határon túl nem érdemes, sőt hátrányos fokozni!
Ha feltesszük azt, hogy egy távolugró esetében adott szakaszon a kérdéses sebességek kapcsolata lineáris (5. ábra), ez a határ számítással könnyen meghatározható (2) alapján.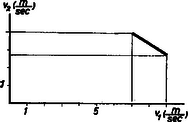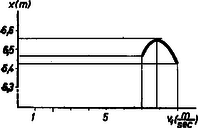

 

 

5. ábra

 

 

6. ábra

 

A számítások eredményét a 6. ábráról olvashatjuk le. Jól látszik, hogy a nekifutás sebességének fokozásával elérkezünk egy határhoz, amelyen túl az ugrás távolsága csökken.

 

Súlypont

 

A távolugrás egyszerű tárgyalását a súlypont szabályos mozgása tette lehetővé. Ismerkedjünk meg részletesebben is az emberi test súlypontjának helyzeteivel.
Mérések alapján megállapították, hogy az emberi test súlyának $7\mathrm{,}1\%$-át a fej, $42\mathrm{,}7\%$-át a törzs, $18\mathrm{,}7\%$-át a láb és $6\mathrm{,}4\%$-át a kar alkotja. (Ha a $100\%$-ot ellenőrizni akarjuk, ne feledjük el, hogy az embernek két karja és két lába van.)
Ezek alapján, valamint a testrészek méreteinek ismeretéből az adódik, hogy egy kb. $180\text{cm}$ magas ember súlypontja $1\text{m}$ magasan van. (Távolugrásnál már történt erre utalás.) Ha tehát egy $80\text{kp}$ súlyú sportoló a $2\mathrm{,}1\text{m}$ magasan levő akadályt (léc) úgy ugorja át, hogy eközben súlypontját is $2\mathrm{,}1\text{m}$ magasra emeli, nem $80\cdot 2\mathrm{,}1\text{mkp}$, hanem csak $80\cdot 1\mathrm{,}1\text{mkp}$ munkát végez.
A test súlypontja magasugrásnál is parabolapályán mozog. Helytelenül gondolkozik tehát az az ugró, aki, hogy súlypontját ,,magasabbra'' vigye, a levegőben felfelé rúg. Vigye pl. a $14\text{kg}$-os láb súlypontját $30\text{cm}$-rel feljebb a $74\text{kg}$-os ugró. A mozgásmennyiség megmaradásának törvénye értelmében

$\begin{array}{c}{\displaystyle x=\frac{14\text{kg}\cdot 0\mathrm{,}3\text{m}}{\left(74-14\right)\text{kg}}=7\text{cm}\mathrm{.}\text{Ennyit süllyed a test!}}\end{array}$

A nekifutás és az elugrás tehát meghatározza a test súlypontjának emelkedését. Ha egyre magasabban elhelyezett akadály fölött akarunk áthaladni, arra kell törekednünk, hogy
a) a súlypont magasságváltozása minél nagyobb legyen,
b) a test súlypontja elrugaszkodáskor minél magasabban legyen,
c) a test az akadály felett olyan alakú legyen, hogy a súlypont az akadályhoz viszonyítva minél mélyebben helyezkedjen el.
Az a)-ban meghatározott követelményre a ,,Hatásfok'' c. részben visszatérünk.
b) A 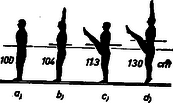$100\text{cm}$ magasan levő súlypont az alapállásban ($7a$. ábra) levő emberre vonatkozik. A kar ($7b$.), a láb ($7c$.), valamint azok együttes lendítésével ($7d$.) a súlypont tetemesen emelkedhet. Ez azt jelenti, hogy az ugró $30\text{cm}$-el fokozhatja az átugrott magasságot, ha végtagjait még a talajon igyekszik magasabbra lendíteni.

 

 

7. ábra

 

c) Ha az ugró az akadály fölött nyújtott testhelyzetben van, súlypontja az akadály fölé, ha $\Delta$ alakban van, az akadály alá jut. Azonos nekifutás és elrugaszkodás, tehát azonos súlypontemelkedés esetén ez azt jelenti, hogy $\Delta$ alakú testtartással az ugró magasabb akadály felett is áthaladhat. (A különbség mérések és számítások szerint a már említett nyújtott és $\Delta$ alakban tört testtartásnál $11\text{cm}$!)

 

Súlypont és munkavégzés

 

Sportolás közben erőkifejtés történik meghatározott úton, a sportoló munkát végez. Mivel az ehhez szükséges energia nem áll rendelkezésre korlátlan mennyiségben és tetszőleges ütemben, a sportolónak arra kell törekednie, hogy mozdulatai aránylag minél kevesebb energiát igényeljenek.
Ha futunk vagy gyalogolunk, energiát vesztünk. Ennek egy részét a súrlódás, a közegellenállás legyőzésére fordítjuk, más részét pedig a test súlypontjának állandó emelésére (8. ábra).

 

 

8. ábra

 

Ha a gyalogló versenyző mozgását figyeljük, azt tapasztaljuk, hogy gyors, de apró léptekkel halad. Ez utóbbi első pillanatra érthetetlennek tűnik, hiszen ha hosszabbakat lépne, még gyorsabban haladna.
Lehetséges azonban, hogy az utóbbi esetben súlypontja, éppen a hosszabb lépés következtében, olyan mértékben süllyed, hogy az emelésekor végzett munka nagyobb, mint a rövid lépések alatt végzett munka. A gyaloglóversenyek távja $20-50\text{km}$, a nagyobb munkavégzés idő előtt felemésztené a versenyző energiáját, s az a távot nem tudná végiggyalogolni.
Haladjon tehát a gyalogló $2h$ hosszúságú pályán úgy, hogy azt $p$ lépésben teszi meg, a lépéshossz $2h/p$, ha $q$ lépésben teszi meg, a lépéshossz $2h/q$.

 

 

9. ábra

 

Tételezzük fel, hogy a 9. ábra első esetének megfelelően mindkét láb, második esetének megfelelően a test súlyát viselő láb teljesen nyújtott, a lábak hossza pedig 1-1 m.
Akkor Pythagoras tételének felhasználásával
a) esetben a súlypont szintváltozása $1-\f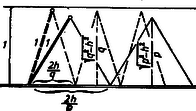rac{\sqrt[]{p^2-h^2}}{p}$ (10. ábra), a teljes munkavégzés $G\cdot \left(1-\frac{\sqrt[]{p^2-h^2}}{p}\right)\cdot p$, míg b) esetben $1-\frac{\sqrt[]{q^2-h^2}}{q}$, ill.

$G\cdot \left(1-\frac{\sqrt[]{q^2-h^2}}{q}\right)\cdot q$. Mindkét esetben $G$ a gyalogló súlya.
Ha $0<p<q$, akkor könnyen bizonyítható, hogy

$G\cdot \left(1-\frac{\sqrt[]{p^2-h^2}}{p}\right)\cdot p>G\cdot \left(1-\frac{\sqrt[]{q^2-h^2}}{q}\right)\cdot q$ és ez a rövidebb lépések ésszerűségét igazolja.

 

 

10. ábra

 

Sífutásnál a távolság szintén tekintélyes (10‐50 km), és így a különböző akadályozó erők ellen tetemes munkavégzés szükséges. A sífutó előrejutását főként karjai erejével segíti elő, a síbotok felhasználásával.
Ha a sífutó versenyző a nem egészen sík, hanem kisebb emelkedőkkel és lejtőkkel tarkított pályán lábaival is segíteni tudja az előrejutást, előnybe kerül csupán karjait igénybe vevő társaival szemben.
Meredek pályán a sílécekkel való lépegetéssel könnyen megvalósítható ez a segítés, kérdés, az enyhe emelkedésű és lejtésű pályán sikló versenyzőnek van-e módja lábai energiáját hasznosítani? (A lépegetés itt hátrányt jelentene!)
Induljunk ki abból a helyzetből, amikor a sífutó egy kis emelkedés tetejéről kezdősebesség nélkül csúszik le a völgybe. Fel tud-e a völgyből siklani egy, az indulás helyével egy szintben levő dombra, ha kezével nem segít? A természetes válasz: nem, mert menet közben pl. a hó és síléc csúszó súrlódása miatt veszít mozgási energiájából, tehát nem juthat fel az eredeti magassággal egy szintre.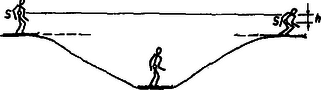

 

 

11. ábra

 

És mégis feljuthat! Ha a domb tetejéről állva siklik le, de a vele egy szintben levő magasságra már guggoló helyzetben ér, a súlypont mélyebbre kerül, mint kiinduláskor (11. ábra), a kettő közötti szintkülönbségből adódó helyzeti energia a súrlódási munkával egyenlő lehet.
Ha a csúszó súrlódási együttható $\mu$, a sportoló tömege $m$, a két testhelyzet súlypontjának szintkülönbsége $h$, akkor az ilyen módon befutható távolság $\left(s\right)$ a következőképpen számítható:

$\begin{array}{c}{\displaystyle P_s=\mu \cdot mg\mathrm{,}{L}_s=\mu \cdot mg\cdot s\mathrm{,}{L}_s=L=mg\cdot h\mathrm{,}}\end{array}$

$s=\frac{h}{\mu }$ a tömegtől, nehézségi gyorsulástól független. $\mu =0\mathrm{,}05$, $h=(1-0\mathrm{,}3\text{m}$ esetén $s=15\text{m}$.
A munkavégzés akkor történik, amikor a guggoló helyzetű versenyző feláll az emelkedés tetején, és most már magasabban elhelyezkedő súlypontja miatt nagyobb helyzeti energiával rendelkezve, újabb távolság befutására képes.

 

 Sümegi László

---

^{${}^{*}$}Középiskolai Matematikai Lapok 1960. évi decemberi sz. 225. old.

^{${}^{*}$}${\alpha }_1$ értelemszerűen $T=2\mathrm{,}6\text{m}-0\mathrm{,}915\text{m}$, ill. $2\mathrm{,}9\text{m}-0\mathrm{,}915\text{m}$ értékek alapján adódott.