Cím: Az 1967. évi Arany Dániel matematikai tanulóversenyek
Füzet: 1967/szeptember, 4 - 8. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Bolyai János Matematikai Társulat a szokásos Arany Dániel tanulóversenyeket ez évben is a Művelődésügyi Minisztérium támogatásával rendezte. Az I. fordulók március 1-én, a II. fordulók május 3-án voltak, mindkétszer 4 órai munkaidővel. Az eddigi szokástól eltérően ebben az évben az I. fordulóból mindkét korcsoport versenyzői 15‐15 feladat közül tetszés szerint választott feladatok megoldása alapján juthattak be a II. fordulóba. Minden egyes versenyző sokszorosítva kézbe kapta a 15 feladat szövegét, valamint azt, hogy az egyes feladatok teljes megoldásával hány pont érhető el. A II. fordulókban a szokás szerint ezidén is 3‐3 feladat volt kitűzve, külön-külön az általános tantervű osztályok versenyzői, illetőleg a szakosított tantervű matematikai osztályok versenyzői részére. A szakosított tantervű matematika‐fizika osztályok tanulói az általános tantervű osztályok versenyében vettek részt, azonban a három feladat közül egyik helyett külön feladatot kellett kidolgozniuk.
A Versenybizottság az I. forduló alapján a II. fordulóra a kezdők korcsoportjában 198, a haladók korcsoportjában 155 versenyzőt hívott be, közülük 49, illetőleg 36 volt valamelyik szakosított tantervű matematikai osztály tanulója.
A versenyek tételei a következők voltak.

 
I. forduló, kezdők részére.
1. Legyen ,,a'' valós szám. Milyen y valós számokra teljesül a következő egyenlőség?
aa+y+ya-yya+y-aa-y=-1.

 
2. Egy vizsgán a tanuló az első 20 kérdésből 15-re helyes választ adott. A további kérdések egyharmadára is helyesen válaszolt. Minden kérdésre azonos pontszámot kapott a tanuló, és így 50%-os eredményt ért el. Hány kérdés volt a vizsgán?
 
3. Árrendezés alkalmával egy cikk ára 40%-kal emelkedett, majd árleszállítás következtében 40%-kal lett olcsóbb. Azóta az ára 126 Ft. Hány Ft volt az eredeti ára?
 
4. Egy derékszögű háromszög átfogóján fekvő külső szögek úgy aránylanak egymáshoz, mint 9:11. Mekkorák a háromszög szögei?
 
5. Egy körbe írt nyolcszög csúcsai rendre A, B, C, D, E, F, G, H. Bizonyítsuk be, hogy az A, C, E és G csúcsoknál levő szögek összege ugyanannyi, mint a további csúcsoknál levő szögek összege.
 
6. Az 1. ábra alapján határozzuk meg az α szög nagyságát, ha tudjuk, hogy AB¯=AC¯ és AD¯=AE¯.
 

 
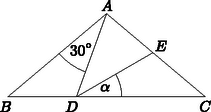1. ábra

 
7. Adott egy háromszögnek egyik csúcsa, a súlypontja és a körülírt kör középpontja. Szerkesszük meg a háromszöget.
 
8. Pista megmagyarázta Józsinak, hogy ha négy egész szám összege páratlan, akkor szorzatuk biztosan páros. Igaz-e ez akkor is, ha öt vagy hat egész számról van szó?
 
9. Melyik az a szám, amelyet hozzáadva 20-hoz, 50-hez és 100-hoz, olyan három számot kapunk, amely közül az első úgy aránylik a másodikhoz, mint a második a harmadikhoz?
 
10. Legyen sc a háromszög c oldalához tartozó súlyvonal és γ a c oldallal szemközti szög. Bizonyítsuk be, hogy γ kisebb, egyenlő, ill. nagyobb 90∘-nál aszerint, hogy sc nagyobb, egyenlő, ill. kisebb, mint c/2.
 
11. A 2. ábrán O a kör középpontja, és a BC¯ szakasz hossza megegyezik a kör sugarával. Milyen határok között változik az α és β szög aránya, ha az AB húrt változtatjuk?
 

 
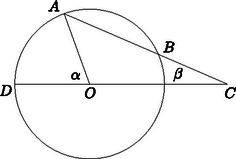2. ábra

 
12. Egy nyári üdülés folyamán 7-szer esett az eső délelőtt vagy délután. Ha délután esett, akkor délelőtt nem esett. Összesen 5 esőtlen délután és 6 esőtlen délelőtt volt. Hány napig tartott az üdülés?
 
13. Milyen pozitív x számokra lesz 2xn>x+1, és milyenekre 2xn<x+1?
 
14. Egy háromjegyű szám számjegyeiből kétféleképpen képeztünk egy-egy új háromjegyű számot. Először az első számjegyet eltoltuk a további két számjegy mögé, másodszor pedig felcseréltük a szélső jegyeket. Először több, mint 200-zal kisebb számot kaptunk az eredeti helyett, másodszor pedig kb. 500-zal kisebbet. Mi lehetett az eredeti szám?
 
15. A P1 sokszögnek minden szöge α. A P2 sokszög minden szöge egyenlő és α-nak egész számú többszöröse. Mekkorák lehetnek P1 szögei, és hány oldalú sokszög lehet P2?
 
Elérhető pontszám ‐ a haladó korcsoportban is ‐ a feladat teljes megoldása esetén: az 1‐7. feladatban 6 pont, a 8‐12. feladatban 8 pont, a 13‐15. feladatban 10 pont volt. Részmegoldásért a nyújtott töredéknek megfelelően kevesebb pontot kaptak a versenyzők.
 
I. forduló, haladók részére.
1. Az ABCD négyszögben az A és D csúcsnál derékszög van, és a négyszög átlói is merőlegesek egymásra. Bizonyítsuk be, hogy
(ABBD)2+(CDAC)2=1.

 
2. Milyen x értékekre veszi fel az alábbi polinom a 0 értéket?
(x2-4)⋅27x⋅(827x3-27).

 
3. Az ABCD négyzet AD oldalán az E pont és az AB oldal meghosszabbításán az F pont úgy helyezkedik el, hogy az ECF szög derékszög. A négyzet területe 256cm2, a CEF háromszög területe 200cm2. Mekkora a BF szakasz?
 
4. Megoldandó a következő egyenlet:
4x2+4x+1-4x2-12x+9=4.

 
5. Az ABCD paralelogramma BC és CD oldalának felezőpontja E és F. Hányadrésze az AEF háromszög területe a paralelogramma területének?
 
6. Tekintsünk egy kétjegyű számot, majd a két jegy közé írjunk egy 0-t, így háromjegyű számhoz jutunk. Határozzuk meg a számokat azzal a feltétellel, hogy az említett kétjegyű és háromjegyű szám számtani közepe egyenlő a kétjegyű szám fordítottjával.
 
7. Egy derékszögű háromszög átfogója 8 cm, az átfogóhoz tartozó magassága 2 cm. Mekkora a befogók aránya?
 
8. Az ABCD téglalapban BC=120m. Az E és az F pont az AD oldalon fekszik és AE=21m, EF=60m. Hogyan kell a BC oldalon a G és a H pontot megválasztani, hogy az EG és FH szakaszok a téglalap területét három egyenlő részre osszák?
 
9. Milyen k értékek mellett lesz az (1) egyenlet mindkét gyöke 5-tel nagyobb, mint a (2) egyenlet egy-egy gyöke?
(1)x2+kx+6=0,(2)x2-kx+6=0.

 
10. Az e és f egyenesek merőlegesen metszik egymást. A két egyenes síkjában fekvő derékszög csúcsa a P pont, egyik szára az e egyenest az A pontban, másik szára az f egyenest a B pontban metszi. Mi a mértani helye az AB felezőpontjainak, ha a derékszög a P pont körül forog?
 
11. Konfundiuszt elküldték, vegyen bizonyos számú fekete és bizonyos számú barna zoknit. A barna fele annyiba került, mint a fekete. Konfundiusz 50%-kal többet adott ki, mint kellett volna, mert felcserélte a fekete és a barna zoknik számát. A rendelt zoknik hányad részének kellett volna feketének lennie?
 
12. Az x milyen értékeinél lesz egész szám a következő kifejezés?
x2+4x-1.

 
13. Egyszerűsítsük az
a4(a-b)(a-c)+b4(b-a)(b-c)+c4(c-a)(c-b)
kifejezést, amelyben a≠b≠c≠a.
 
14. Egy szög csúcsa A, a szögfelező egy pontja B. Egy A-n és B-n átmenő kör a szög száraiból h1 és h2 hosszúságú húrt metsz ki. Bizonyítsuk be, hogy hl+h2 minden körre ugyanakkora.
 
15. Számítsuk ki a következő kifejezés értékét:
1+x1+1+x+1-x1-1-x,hax=32.

 
II. forduló, kezdők korcsoportja, általános tantervű osztályok részére.
1. a és b milyen értékei mellett van megoldása az
x-ax-2+x-bx-3=2
egyenletnek? Milyen a és b értékek mellett egyértelmű a megoldás?
 
2. Szerkesszünk háromszöget, ha ismert az egyik szögfelező hossza, a másik két csúcsnál levő szögek különbsége és a szögfelező melletti oldalak közül a nagyobbik.
 
3. Hányféleképpen lehet kiválasztani egy kocka csúcsai közül négyet? Nem tekintünk különbözőnek két kiválasztást, ha egyik a másikba forgatással vagy tükrözéssel átvihető.
 
A szakosított tantervű matematika‐fizikai osztályok tanulói az 1. feladat helyett a következő feladatot kapták:
 
4. Milyen k és n egész számokra lesz a következő tört értéke egész?
T=(k2+n)(1+n)+n2k2+1(k2-n)(1-n)+n2k2+1.

 
II. forduló, kezdők korcsoportja, szakosított tantervű matematikai osztályok részére.
1. Azonos az előző felsorolás 4. feladatával.
 
2. Adott egy tetszés szerinti négyszög. Hogyan szerkesztjük meg azt a legkisebb sugarú kört, amely lefedi a négyszöget?
 
3. Az ABCDE konvex ötszög minden egyes oldalát és átlóját piros vagy kék színnel úgy kell megrajzolnunk, hogy bármelyik három csúcs által meghatározott háromszög kerületén mindkét szín előforduljon. Hányféleképpen tehetjük ezt meg?
 
II. forduló, haladók korcsoportja, általános tantervű osztályok részére.
1. Valamely kétjegyű számot megszorozva számjegyeinek összegével, eredményül a jegyek köbeinek összegét nyerjük. Mi lehet ez a szám?
 
2. Milyen határok közé eső valós értékeket vesz fel az alábbi kifejezés?
y=ab2-c2-cb2-a2b2.

 
3. Az ABC háromszög CA oldalát megrövidítjük az AA' szakasszal, CB oldalát pedig ugyanekkora BB'-vel meghosszabbítjuk (BB'=AA'). Az A'B' egyenes az AB oldalt az E pontban metszi. Bizonyítsuk be, hogy
A'E:EB'=CB:CA.

 
A matematika‐fizikai osztályok versenyzőinek az 1. feladat helyett a következőt kellett kidolgozniuk:
 
4. Egy szabályos hatszög egyik oldala AB, a hatszög belsejének vagy kerületének egy pontja C. A C pont mely helyzetében lesz az ABC háromszög kerülete a legnagyobb?
 
II. forduló, haladók korcsoportja, szakosított tantervű matematikai osztályok részére. 1. Keressünk természetes számokból álló olyan növekvő sorozatot, amelyikben bármely két egymás után következő tag összege egyenlő különbségük négyzetével.
 
2. Legfeljebb hány ismeretség lehet egy n tagú társaságban, ha bármelyik két olyan emberhez, akik ismerik egymást, van a társaságnak legalább egy olyan tagja, akit egyikük sem ismer?
 
3. Azonos az előző felsorolás 3. feladatával.
 
A versenyek eredménye

 
A) Kezdők versenyei

 
A 1. Az általános tantervű osztályok versenyének mindhárom feladatát megoldotta, a másodikat kisebb hiányossággal ‐ és I. díjban, 250 Ft jutalomban részesült
Bajmóczy Ervin (Budapest, Ady Endre közös igazgatású iskola ált. isk. 8. o. tanulója, tanára: Kálmán Attila).
Mindhárom feladatot megoldotta, de az első kettőt kisebb hiányossággal, és ezért II. díjban, 200 Ft jutalomban részesült
Győry György (Debrecen, KLTE Gyak. Gimn., tanára: Vikár István).
Mindhárom feladattal eredményesen foglalkoztak, és ezért III. Díjban, 100‐100 Ft jutalomban részesültek:
Lempert László (Bpest, Radnóti M. Gyak. Gimn., tanára: Cserepkei Ferenc),
Nyikos István (Bpest, Eötvös J. Gimn., tanára: Imrecze Zoltán),
Walthier Tamás (Bpest, Piarista Gimn., tanára: Szoboszlay András).
 
További három tanuló kiemelkedő munkájáért elsó dicséretben és 50 Ft-os könyvutalványban részesült; betűrendben felsorolva: Kabos Sándor (Bp., Radnóti M. Gyak. Gimn., tanára: Cserepkei Ferenc), Thurnherr Kálmán (u. az), Vértes András (Bp., Apáczai Csere J. Gyak. Gimn., tanára: Czapáry Endre).
Második dicséretben és oklevélben részesültek egyenlő helyezéssel, betűrendben felsorolva: Cserepes László (Bp., Piarista G., tanára: Kovács Mihály), Fehér Sándor (Kisújszállás, Móricz Zs. G., tanára: Fülöp Gábor), Láz József (Bp., Eötvös J. G., tanára: Imrecze Zoltán), Loványi István (u. az), Ormos Pál (Tatabánya, Árpád G., tanára: Várnagy Istvánné), Vadász István (Sopron, Martos Flóra G., tanára: Gerencsér Miklósné), Hornung János (Bp., Apáczai Csere J. Gyak. G., tanára: Czapáry Endre).
 
A 2. A szakosított tantervű matematikai osztályok versenyén a versenybizottság I. díjat nem adott ki. Az első és harmadik feladat teljes megoldásáért és a második feladattal való eredményes foglalkozásért II. díjban, 200‐200 Ft jutalomban részesült:
Borzsák Péter (Budapest, I. István Gimn., tanárai: Jelitay Árpád, Rácz János, Móró Károly), és
Kóczy László (Budapest, Fazekas M. Gyak. Gimn., tanárai: Thiry Imréné és Kardos Gyula).
 
Két feladatban kiemelkedőt nyújtott és ezért első dicséretben és 50 Ft-os könyvutalványban részesült, betűrendben felsorolva: Kálmán Miklós (Fazekas Gimn.), Pataki János (Bp., Berzsenyi D. G., tanárai: Herczeg János és Ratkó István), Prőhle Tamás (Fazekas Gimn.).
Második dicséretben és oklevélben részesült, egyenlő helyezéssel, betűrendben felsorolva: Ács Júlia (Fazekas G.), Barbarits István (I. István G.), Beck József (I. István G.), Havril Katalin (Fazekas G.), Kéhli Erika (Berzsenyi G.).
 
B) Haladók versenyei

 
B 1. Az általános tantervű osztályok versenyén mindhárom feladat megoldásáért I. díjat, 250 Ft jutalmat nyert
Andor László (Budapest, II. Rákóczi F. Gimn., tanára: Vigassy György).
Két feladat ‐ köztük a legnehezebbnek bizonyult 2. feladat különösen szép megoldásáért II. díjat, 200 Ft jutalmat nyert
Michaletzky György (Budapest, Piarista Gimn., tanára: Pogány János).
Két feladat szép megoldásáért III. díjat, 100 Ft jutalmat nyert
Hárs László (Budapest, Kölcsey F. Gimn., tanára: Hidvégi Imre).
Két feladat helyes megoldásáért vagy ezzel egyenlő értékű teljesítményükért első dicséretben részesültek, 50 Ft-os könyvutalványt és oklevelet kaptak: Kálmán Péter (Bp., Apáczai Csere J. Gyak. G., tanára: Nagy Jánosné), Kovalszky Róbert (Bp., Landler J. G., tanára: Kerékgyártó Jenő), Krasznai Andor (Gyöngyös, Vak Bottyán G., tanára: Rónai Kálmán), Lányi Tamás (Székesfehérvár, Ságvári E. Gép- és Hír. ip. Technikum, tanára: Dr. Petrusz Béla), Nagy András (Bp., Toldy F. G., tanára: Huba Árpád), Németh Iván (Pannonhalma, Bencés G., tanára: Vida Szabolcs), Tél Tamás (Bp., Apáczai Csere J. G.).
Két feladat megoldását megközelítő teljesítményükért második dicséretben részesültek és oklevelet kaptak: Bálványos Zoltán (Makó, József A. G., tanára: Domokos Géza), Berbekár György (Bp., Eötvös J. G., tanára: Imrecze Zoltán), Dörfner Péter (Várpalota, Thuri Gy. G., tanára: Szabó Gyula), Erdős Géza (Bp., József A. G., tanára: Horváth Józsefné), Háy György (Bp., Eötvös J. G.), Jánossy Dániel (Bp., Eötvös J. G.), Józsa Zsuzsanna (Bp., Eötvös J. G., tanára: Gara Ernőné), Glódy István (Bp., Ságvári E. Gyak. G., tanára: Reményi Gusztávné), Sain Ildikó (Bp., Apáczai G.), Stachó László (Szeged, Radnóti M. G., tanára: Bánfalvi Józsefné), Stefanovicz Károly (Bp., Veres Pálné G., tanára: Kelemen Zoltánné), Váradi József (Bp., Ságvári E. G.), Zákány Gábor (Bp., Apáczai G.), Zöllei István (Szeged, Radnóti G.).
 
B 2. A szakosított tantervű matematikai osztályok versenyén négy tanuló lényegében mindhárom feladatot megoldotta. Az első feladat megoldása teljességéért és a legnehezebbnek bizonyult második feladat megoldásáért I. díjat és 250‐250 Ft jutalmat nyertek:
Csirmaz László (Budapest, I. István Gimn., tanára: Rácz János),
Pintz János (Budapest, Fazekas M. Gyak. G., tanára: Reményi Gusztáv).
A második feladat különösen szép megoldásáért II. díjat nyert és 200 Ft jutalmat kapott
Soós Miklós (Fazekas Gimn.).
A 2. feladat szép megoldásáért III. díjat, 100 Ft jutalmat nyert
Soltész János (Fazekas Gimn.).
 
Két feladat helyes megoldásáért vagy ezzel egyenlő értékű teljesítményükért dicséretben részesültek és oklevelet kaptak: Békéssy Péter (Bp., Berzsenyi D. G., tanárai: Pogáts Ferenc, Ratkó István, Oláh Gyuláné), Csobádi Péter (Berzsenyi), Erdődy Gabriella (Fazekas), Dévényi Károly (Fazekas), Köpf Vilmos (Berzsenyi), Lengyel Tamás (Berzsenyi), Máté Lajos (I. István G.), Missik Éva (Berzsenyi), Nagy Miklós (Fazekas), Pataki István (Fazekas), Siklósi Miklós (Berzsenyi), Somogyi Árpád (Fazekas).
Kimutatás a II. fordulóba bejutott versenyzők számáról megyék, városok szerint: Bács-Kiskun: 4 kezdő, 1 haladó (röviden: 4, 1); Baranya, Pécs: 8, 4; Békés: 2, 2; Borsod-Abaúj-Zemplén, Miskolc: 4, 7; Csongrád, Szeged: 8, 8; Fejér: 5, 5; Győr-Sopron: 9, 6; Hajdú, Debrecen: 6, 3; Heves: 4, 3; Komárom: 9, 0; Nógrád: 0, 0; Pest: 7, 1; Somogy: 3, 4; Szabolcs-Szatmár: 4, 2; Szolnok: 3, 1; Tolna: 3, 0; Vas: 2, 6; Veszprém: 9, 6; Zala: 5, 1; Budapest: 103, 95.