Kezdőlap


Cím:	Jelentés a Középiskolai Matematikai Lapok 32. kötetének 5. számában közzétett pályázatról
Szerző(k):	Bakos Tibor , Fried Ervin , Tusnády Gábor
Füzet:	1967/május, 205 - 212. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Lapunk a 32. kötet 5. (1966/5 220. old.) számában pályázatot hirdetett 1966. november 15-i határidővel a következő tétel kidolgozására:
I. Milyen összefüggés áll fenn egy háromszög oldalainak mértékszámai között, ha a háromszög beírt köre áthalad a súlyponton?
II. Vannak-e az ilyen háromszögek közt olyanok, amelyek oldalainak a mértékszáma alkalmas mértékegységgel mérve egész szám?
III. Két csúcsot rögzítve vázolandó, milyen görbén mozog a harmadik.

A pályázatra 6 dolgozat érkezett. Közülük három lényegében megoldotta a feladatot, sőt a tétel II. részkérdésére megadta az összes megfelelő háromszögek előállítását, vagy legalább végtelen sok, nem hasonló háromszöget adott meg. Gondosabb kidolgozásuk, megfogalmazásuk alapján egyenlő helyezéssel 1. díjban, 100‐100 Ft értékű könyvutalványban részesültek:

Csirmaz László (Budapest, I. István gimn. II. o. t.) és
Tihanyi László (Makó, József A. gimn. IV. o. t.).

2. díjban, 50 Ft-os könyvutalványban részesült
Korchmáros Gábor (a budapesti Rákóczi F. Gimn. 1966-ban érettségizett tanulója).

A további 3 dolgozat nem ad teljes megoldást, nem foglalkozik a III. részkérdéssel. Szerzőik:

Balogh József (Hatvan, Bajza J. gimn. IV. o. t.),
Fiala Tibor (Budapest, Rákóczi F. g. II. o. t.) és
Gáspár András (Budapest, Vasútgépészeti techn. IV. o. t.)
dicséretben részesültek.

Az alábbiakban a kitűzött tétel egy megoldását adjuk, a dolgozatok egyes részeit felhasználva, egyszerűsítve és kiegészítve.
I. Legyen az

A B C

háromszög

A B

oldalának felezőpontja

F

, az

A

B

C

csúccsal szemben levő oldal hossza rendre

a

b

c

, a

C F

súlyvonal hossza

d

, és

C

-nek

F

-re vonatkozó tükörképe

D

(1. ábra). Ekkor az

A C B D

paralelogramma

a

b

oldalai, valamint

c

és

C D = 2 d

átlói közötti ismert összefüggés alapján fennáll

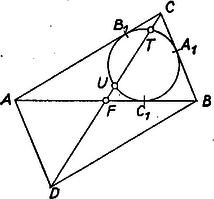\begin{matrix} 2 a^{2} + 2 b^{2} = c^{2} + {(2 d)}^{2}, d^{2} = \frac{2 a^{2} + 2 b^{2} - c^{2}}{4} . \end{matrix}

(1)

1. ábra

Jelölje a háromszögbe írt kör érintési pontját az

A

B

C

csúccsal szemben levő oldalon rendre

A_{1}

B_{1}

C_{1}

, az

A B_{1} = A C_{1}

B C_{1} = B A_{1}

és

C A_{1} = C B_{1}

érintőszakaszok közös hosszát rendre

x

y

, illetőleg

z

, a háromszög kerületét

2 s

, ekkor

\begin{matrix} x + y = c; y + z = a, z + x = b, amiből & (2) \\ x + y + z = s, x = s - a, y = s - b, z = s - c = \frac{a + b - c}{2} . & (3) \end{matrix}

Messe a

C F

súlyvonal a beírt kört a

T

U

pontokban és legyen

C T / C F = α

, azaz

C T = α \cdot d

, hasonlóan

C U = β \cdot d

. A körhöz külső pontból húzott szelőn és érintőn előálló szakaszok közti összefüggést

C

-re és

F

-re alkalmazva

\begin{matrix} C T \cdot C U = C A_{1}^{2}, F T \cdot F U = F C_{1}^{2} . \end{matrix}

(4)

Itt

F C_{1} = F B - B C_{1} = | (b - a) / 2 |

, így (3) alapján

\begin{matrix} α β = {(\frac{a + b - c}{2 d})}^{2}, (1 - α) (1 - β) = {(\frac{b - a}{2 d})}^{2} . \end{matrix}

(5)

A második összefüggésből, az elsőt, valamint (1)-et felhasználva

\begin{matrix} - (α + β) & = {(\frac{b - a}{2 d})}^{2} - 1 - α β = \frac{1}{4 d^{2}} [{(b - a)}^{2} - 4 d^{2} - {(a + b - c)}^{2}] = \\ = - \frac{1}{2 d^{2}} (a + b) (a + b - c), \end{matrix}

ennélfogva

α

és

β

a következő másodfokú egyenlet gyökei:

\begin{matrix} (2 a^{2} - 2 b^{2} - c^{2}) ξ^{2} - 2 (a + b) (a + b - c) ξ + {(a + b - c)}^{2} = 0. \end{matrix}

(6)

A beírt kör akkor és csak akkor halad át a háromszög

S

súlypontján, ha

T

és

U

valamelyike azonos

S

-sel,

α

és

β

egyike egyenlő

C S / C F = 2 / 3

-dal, vagyis ha

ξ = 2 / 3

kielégíti (6)-ot:

\begin{matrix} (2 a^{2} + 2 b^{2} - c^{2}) \cdot {(\frac{2}{3})}^{2} - 2 (a + b) (a + b - c) \cdot \frac{2}{3} + {(a + b - c)}^{2} = 0. \end{matrix}

(7)

Ez a keresett összefüggés az oldalak mértékszámai között. Itt

a

b

és

c

szerepe nem szimmetrikus; a feladat kirovásában viszont egyik oldalnak sincs kitüntetett szerepe, ezért ugyanez várható a keresett összefüggésben is. Alkalmas rendezéssel azonban a várakozásnak megfelelő alakra hozhatjuk (7)-et:

\begin{matrix} 5 (a^{2} + b^{2} + c^{2}) = 6 (a b + a c + b c), \end{matrix}

(8)

ezt tekintjük a keresett összefüggés végleges alakjának.
Egyenlő szárú háromszögben,

C A = C B

, azaz

b = a

esetére

C_{1}

azonos

F

-fel,

T

és

U

egyike is ide esik,

α

és

β

egyike 1, (4) második összefüggése semmitmondó. A (8)-ból adódó

4 a^{2} - 12 a c + 5 c^{2} = 0

egyenlet (5)-ből is kiadódik

α β = 2 / 3

előírásával. Innen

c' = 2 a / 5

és

c'' = 2 a

, az utóbbi érték egyenesszakasszá elfajult egyenlő szárú háromszöget ad.

II. Az imént láttuk, hogy a (8)-at kielégítő egyenlő szárú háromszög szárának és alapjának aránya az

5 / 2

racionális szám, eszerint ha

t

természetes szám, akkor

5 t

5 t

2 t

máris egy megfelelő háromszög oldalai.
A feladat kérdésén túlmenve előállítjuk a (8)-at kielégítő összes

a

b

c

egész számhármasokat, majd megmutatjuk, hogy minden ilyen számhármashoz tartozik háromszög.
Tegyük fel, hogy

a

b

c

egész számok, és adjunk (8) mindkét oldalához

3 (a^{2} + b^{2} + c^{2})

-et:

\begin{matrix} 8 (a^{2} + b^{2} + c^{2}) = 3 {(a + b + c)}^{2} . \end{matrix}

Itt a bal oldal páros szám, ezért a jobb oldalon

{(a + b + c)}^{2}

is páros, ami csak úgy lehet, ha

a + b + c

is páros. Ekkor (3)-ban

s

, továbbá

x

y

z

ugyancsak egész számok. Fordítva, ha

x

y

z

egész számok, akkor (2)-bő1

a

b

c

is egészek. És mivel

x

y

z

-re (8)-nál egyszerűbb egyenlet teljesül, ugyanis (2)-t (8)-ba helyettesítve

\begin{matrix} x^{2} + y^{2} + z^{2} = 2 (x y + x z + y z), \end{matrix}

(9)

azért ezen egyenlet összes egész megoldásait állítjuk elő. Továbbmenve elég meghatározni a (9)-et kielégítő

x

y

z

egész számhármasok közül csupán azokat, amelyek tagjainak nincs (valódi) közös osztójuk, ezeket (9) alapmegoldásainak nevezzük. Nyilvánvaló ugyanis, hogy (9) egy egész megoldásából új megoldást kapunk, ha a számokat rendre szorozzuk egy tetszés szerinti

t

egész számmal, valamint akkor is, ha a számokat rendre osztjuk a három szám egy

d

közös osztójával, természetesen amennyiben van közös osztójuk. Eszerint minden megoldás vagy alapmegoldás, vagy leszármaztatható szorzás útján egy alapmegoldásból.
Alapmegoldás bármelyik két száma egymáshoz relatív prím. A szimmetria miatt elég ezt belátni, pl. az

x

y

számpárra. Ha

x

és

y

nem lennének relatív prímek, akkor lenne (1-nél nagyobb)

d

közös osztójuk. Vegyük ennek legkisebb (valódi) osztóját, ez mindenesetre prím, jelöljük

p

-vel. Ez osztója volna

x

-nek is,

y

-nak is, ezért (9) jobb oldala, valamint bal oldalának első két tagja osztható lenne

p

-vel, tehát a harmadik tag,

z^{2}

is osztható lenne vele.

p

prím volta miatt ez csak úgy volna lehetséges, ha maga

z

is osztható lenne

p

-vel. Ez pedig ellentmond annak, hogy

x

y

z

alapmegoldás. Ezzel igazoltuk állításunkat.
Alapmegoldásban nem lehet

x

y

z

mindegyike páros, feltehetjük tehát, hogy

z

páratlan. Írjuk (9)-et a következő alakban:

\begin{matrix} {(x - y)}^{2} = (2 x + 2 y - z) \cdot z . \end{matrix}

(10)

Itt a jobb oldal tényezői egymáshoz relatív prímek. Ha ugyanis a

p

prímszám közös osztójuk volna, akkor összegük,

2 x + 2 y

is osztható volna

p

-vel; másrészt így a bal oldal is osztható volna

p

-vel, tehát maga

x - y

is. Ekkor pedig

2 x + 2 y

-hoz

2 (x - y)

-t akár hozzáadva, akár belőle ezt kivonva ismét

p

-vel osztható számot kapnánk, vagyis

4 x

is,

4 y

is, és ezért maga

x

és

y

is osztható volna

p

-vel ‐ hiszen

z

páratlan volta miatt

4

nem osztható

p

-vel ‐, tehát

p

közös osztója volna

x

y

z

mindegyikének, amit kizártunk.
Most már ‐ mivel (10) bal oldala négyzetszám ‐ a jobb oldal tényezői külön‐külön négyzetszámok:

\begin{matrix} 2 x + 2 y - z = u^{2}, z = v^{2}, \end{matrix}

(11)

mégpedig az első is páratlan, így

u

és

v

páratlan, egymáshoz relatív prím számok; előjelük lényegtelen, ezért vehetjük mindkettőjüket pozitívnak. Ezekkel (10) így alakul:

{(x - y)}^{2} = u^{2} v^{2}

, amiből

\begin{matrix} x - y = u v . \end{matrix}

(12)

A jobb oldal előjelének megválasztásával az

x > y

korlátozást vezettük be, ami a szimmetria miatt nem lényeges. Végül (11)-ből és (12)-ből:

\begin{matrix} x = {(\frac{u + v}{2})}^{2}, y = {(\frac{u - v}{2})}^{2}, z = v^{2} . \end{matrix}

(13)

A behelyettesítés szerint (13) kielégíti (9)-et. Másrészt, ha

u

v

pozitív páratlan, egymáshoz relatív prím számok, akkor

x

y

z

egészek, továbbá a fentebbiekhez hasonlóan belátható, hogy nincs közös osztójuk, tehát (13) alapmegoldása (9)-nek.
Mindezek szerint (8) minden egész megoldása a következő alakban állítható elő:

\begin{matrix} a & = [{(\frac{u - v}{2})}^{2} + v^{2}] \cdot t, b = [{(\frac{u + v}{2})}^{2} + v^{2}] \cdot t, & (14) \\ c & = [{(\frac{u + v}{2})}^{2} + {(\frac{u - v}{2})}^{2}] \cdot t = \frac{u^{2} + v^{2}}{2} \cdot t, \end{matrix}

ahol

u

v

pozitív, páratlan, egymáshoz relatív prím számok, és

t

tetszés szerinti egész szám.
Hátra van még annak belátása, hogy (14) mindig egy háromszög oldalmértékszámait adja ‐ természetesen, ha

t

pozitív. Ez abból adódik, hogy (2) szerint

\begin{matrix} a + b - c = 2 z, b + c - a = 2 x, c + a - b = 2 y, \end{matrix}

és ezek (13) szerint pozitív számok, a háromszög‐egyenlőtlenség teljesül.

\begin{matrix} v & u & x & y & z & a & b & c \\ 1 & 3 & 4 & 1 & 1 & 2 & 5 & 5 & E \\ 5 & 9 & 4 & 1 & 5 & 10 & 13 & F \\ 7 & 16 & 9 & 1 & 10 & 17 & 25 & G \\ 3 & 1 & 4 & 1 & 9 & 10 & 13 & 5 & F \\ 5 & 16 & 1 & 9 & 10 & 25 & 17 & G \\ 7 & 25 & 4 & 9 & 13 & 34 & 29 & H \\ 5 & 1 & 9 & 4 & 25 & 29 & 34 & 13 & H \end{matrix}

A táblázat néhány számpéldát tartalmaz.

t

értéke minden esetben 1, hiszen nagyobb értékeivel ugyanezen háromszögeknek csupán

t

-szeres nagyítását kapjuk. Mindjárt feltűnik, hogy az

F

G

H

jelű, páronként egybevágó háromszögeket különböző

u

v

értékpárokból is megkaptuk az oldalak más sorrendjével. Bár az ilyen ismétlődések vizsgálatát már nem tekintjük feladatunknak, mégis röviden két megjegyzést teszünk.
Az ismétlődés közvetlen oka az

x

y

z

értékek megismétlődése valamely más sorrendben.

x

és

y

egyike (12) miatt páros, másika páratlan,

z

helyére csak a páratlan kerülhet közülük, így ugyanazt a háromszöget pozitív

u

és

v

értékekre szorítkozva csak két értékpárból kapjuk meg. (Az

E

egyenlő szárú háromszöget pedig csak az

u = 3

v = 1

-ből).

v

-t rögzítve nem adódik ismétlődés. Pl.

v = 1

esetén minden

u = 2 k + 1

szám sorra vehető, amelyben

k \geq 1

, természetes szám, és az

\begin{matrix} x = {(k + 1)}^{2}, y = k^{2}, z = 1 \end{matrix}

(15)

számhármasok csupa páronként nem hasonló háromszöget adnak.
Mindezek szerint végtelen sok olyan, páronként nem hasonló háromszög van, melynek beírt köre átmegy a súlypontján, és oldalai egész számok.

Megjegyzés. A (14) megoldás előállítható a jól ismert pitagoraszi számhármasokra vonatkozó eredmények alapján is, hiszen (10) jobb oldala írható két négyzet különbségeként:

\begin{matrix} {(x - y)}^{2} = {(x + y)}^{2} - {(x + y - z)}^{2} . \end{matrix}

A (10)-re alkalmazott gondolatmenet használatos a pitagoraszi egyenlet

2 m n

m^{2} - n^{2}

m^{2} + n^{2}

(

m

n

relatív prímek, egyikük páros) megoldásának előállításában is.

III. Rögzítsük a háromszög

A

B

csúcsait és mozgassuk a

C

csúcsot úgy, hogy mindig teljesüljön (8). A pálya nyilvánvalóan szimmetrikus az

A B

szakasz felező merőlegesére, úgyszintén az

A B

egyenesre is. Legyen

A B = c = 1

, ekkor a

C

pont

B C = a

és

A C = b

vezérsugaraira (8)-ból

\begin{matrix} 5 b^{2} - 6 (a + 1) b + (5 a^{2} - 6 a + 5) = 0, amiből & (16) \\ b_{1,2} = \frac{1}{5} (3 a + 3 \pm 4 \sqrt[]{- a^{2} + 3 a - 1}) . & (17) \end{matrix}

Csak olyan

a

értékekhez kapunk valós

b

-t, amelyekre a diszkrimináns nem negatív:

\begin{matrix} - a^{2} \cdot 3 a - 1 \geq 0, vagyis \frac{3 - \sqrt[]{5}}{2} \leq a \leq \frac{3 + \sqrt[]{5}}{2}, \end{matrix}

(18)

és minden ilyen

a

esetén a (17) értékek pozitívok, hiszen (16) együtthatói szerint összegük is, szorzatuk is pozitív:

\begin{matrix} b_{1} + b_{2} = \frac{6 (a + 1)}{5} > 0, \\ b_{1} b_{2} = a^{2} - \frac{6}{5} a + 1 = {(a - \frac{3}{5})}^{2} + \frac{16}{25} > 0. \end{matrix}

Bármely, a (18)-nak eleget tevő

a

-val és a (17) szerinti

b_{1}

b_{2}

értékekkel adódó

a_{1}

b_{1}

és

a_{2}

b_{2}

értékpárhoz tartozik

C

pont a síkon; ez a II. rész utolsó meggondolásából adódik,

t = 1

-re szorítkozva és eltekintve attól a korlátozástól, hogy

a

b

x

y

z

u

és

v

egész számok. Ezek szerint

C

csak a

B

csúcs körül

\begin{matrix} r = a_{min} = \frac{3 - \sqrt[]{5}}{2} (\approx 0, 382) és R = a_{max} = \frac{3 + \sqrt[]{5}}{2} (\approx 2, 618) \end{matrix}

sugárral írt körök közti körgyűrű‐tartományban mozoghat, és

r < a < R

esetén a

B

körüli,

a

sugarú körön, az

A B

egyenes mindegyik oldalán 2 pontja van a pályának.

\begin{matrix} a = r \end{matrix}

A szimmetria miatt

C

A

körüli

r

és

R

sugarú körök közti gyűrűtartományból sem léphet ki.

C

pályájának egyes pontjait kijelölhetjük a fenti táblázat háromszögei alapján is, úgy kicsinyítve őket, hogy valamelyik oldaluk mértékszáma

A B = 1

legyen; ekkor

C

helyzetét a másik két oldallal mint sugárral

A

, ill.

B

körül írt körök metszéspontja adja. Minden oldalhármas

3 \cdot 4 = 12

pontot ad a pályából, mert az

A B

-re illesztendő oldal 3-féleképpen választható (kivéve

E

-t, ez a szimmetria miatt csupán 6 pontot). Pl. a táblázat

F

háromszögét

1 : 5

, ill.

1 : 10

, ill.

1 : 13

arányban kicsinyítve az oldalak

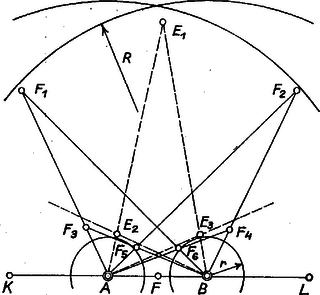\begin{matrix} 1, 2, \frac{13}{5}; \frac{1}{2}, 1, \frac{13}{10}; \frac{5}{13}, \frac{10}{13}, 1. \end{matrix}

2. ábra

Az adódó

A B F_{1}

A B F_{2}

...

A B F_{6}

háromszögek hasonlók, ezért

C

-nek az

A B

egyenes ugyanazon oldalán adódó 6 helyzete párosával 3‐3 az

A

-ból,

B

-ből kiinduló félegyenesen helyezkedik el, hiszen a félegyenesek

A B

-vel,

B A

-val bezárt szöge csak 3 értéket vehet fel (2. ábra). Az ugyanazon félegyenesen levő oldalak a hasonlóság miatt egymás reciprokai:

A F_{1} \cdot A F_{3} = A F_{5} \cdot A F_{2} = A F_{6} \cdot A F_{4} = 1

. Ugyanez áll bármely megfelelő, nem egyenlő szárú háromszögből szerkeszthető ponthatos esetén, így a pályának bármely, az

A

-ból kiinduló (és nem az

A B

egyenesbe eső) félegyenesen, ha egyáltalán van pontja, akkor 2 pontja van. A táblázat

E

háromszögéből adódó

A E_{3}

B E_{2}

félegyeneseken azonban csak 1‐1 pontot biztosít ez a meggondolás.
A pálya bármely

C

pontjának

C B

C A

távolságait egyszerű szerkesztéssel kaphatjuk az alábbi úton. Az

x

y

szakaszokat úgy választva, hogy

x + y = A B = c

legyen, (9)-ből

\begin{matrix} {(x + y - z)}^{2} = 4 x y, z_{1,2} = x + y \mp 2 \sqrt[]{x y} = c \mp 2 \sqrt[]{x y}, \\ a_{1} = y + z_{1} = y + c - 2 \sqrt[]{x y}, a_{2} = y + c + 2 \sqrt[]{x y}, \\ b_{1} = x + z_{1} = x + c - 2 \sqrt[]{x y}, b_{2} = x + c + 2 \sqrt[]{x y} . \end{matrix}

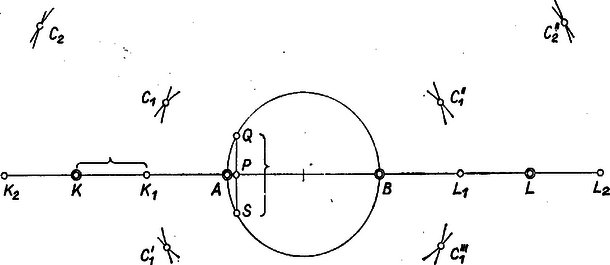3. ábra

Legyen

K

L

A B

egyenesnek az a pontja, amelyre

K A = A B = B L

, továbbá

P

A B

szakasznak az a pontja, amelyre

A P = x

P B = y

(3. ábra). Rajzoljunk

A B

fölé Thalész‐kört és húzzuk meg benne

P

-n át az

A B

-re merőleges

Q S

húrt, ekkor

K P = c + x

P L = c + y

, és

Q S = 2 \sqrt[]{x y}

, továbbá mérjük fel

Q S

-et az

A B

egyenesre

K

-tól és

L

-től mindkét irányban, legyenek a végpontok

K_{1}

K_{2}

L_{1}

L_{2}

úgy, hogy

A K_{1} < A K_{2}

B L_{1} < B L_{2}

, ekkor a fentiek szerint

a_{1} = P L_{1}

b_{1} = P K_{1}

, ill.

a_{2} = P L_{2}

b_{2} = P K_{2}

.
Az alábbiakkal szemléletes alátámasztását kívánjuk adni a következő sejtésnek: minden az

A

-ból kiinduló, nem az

A B

egyenes részét képező félegyenesen van a pályának legalább 2 pontja, más szóval, hogy megfelelő háromszögeink szögei között minden

0^{\circ}

és

180^{\circ}

közti szög előfordul. Ebből adódik az a további sejtés, hogy a pálya folytonos vonal.
A (15) képletek szerinti

\begin{matrix} x = s - a = {(k + 1)}^{2}, y = s - b = k^{2}, z = s - c = 1, \\ a = 1 + k^{2}, b = 1 + {(k + 1)}^{2}, c = k^{2} + {(k + 1)}^{2} \end{matrix}

oldalhármas, az egész számokra vonatkozó követelményt mellőzve minden pozitív

k

esetén eleget tesz (8)-nak. Ebben a

c

oldallal szemben fekvő

γ

szögre

\begin{matrix} sin^{2} \frac{γ}{2} = \frac{(s - a) (s - b)}{a b} = \frac{k^{2}}{1 + k^{2}} \cdot \frac{{(k + 1)}^{2}}{1 + {(k + 1)}^{2}} . \end{matrix}

(19)

Itt az első tényező

k

növekedésével nő, mert ha

k_{2} > k_{1} \geq 0

, akkor

\begin{matrix} \frac{k_{2}^{2}}{1 + k_{2}^{2}} - \frac{k_{1}^{2}}{1 + k_{1}^{2}} = \frac{k_{2}^{2} - k_{1}^{2}}{(1 + k_{2}^{2}) (1 + k_{1}^{2})} > 0, \end{matrix}

és minden

0 \leq ϑ < 1

értéket felvesz, ti.

k = \sqrt[]{ϑ / (1 - ϑ)}

esetén. Továbbá 1-től való eltérése tetszés szerinti kicsivé tehető azáltal, hogy

k

-t elég nagyra választjuk; ha ugyanis

ε

tetszés szerinti pozitív szám, akkor

\begin{matrix} 1 - \frac{k^{2}}{1 + k^{2}} = \frac{1}{1 + k^{2}} < ε, mihelyt k^{2} > \frac{1}{ε} - 1. \end{matrix}

Hasonlóan (19) második tényezője a

k \geq 0

értelmezési tartományban felvesz minden

0, 5 \leq ϑ < 1

értéket. (19) jobb oldalának 1-től való eltérése is tetszés szerinti kicsivé tehető, mert második tényezőjét is az első tényezővel helyettesítve

\begin{matrix} sin^{2} \frac{γ}{2} > {(\frac{k^{2}}{1 + k^{2}})}^{2}, és így 0 < ε < 1 esetén \\ 1 - sin^{2} \frac{γ}{2} < 1 - {(\frac{k^{2}}{1 + k^{2}})}^{2} ε, mihelyt k^{2} > \frac{\sqrt[]{1 - ε}}{1 - \sqrt[]{1 - ε}} . \end{matrix}

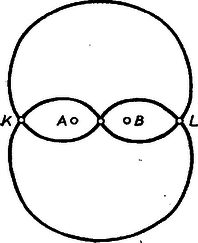4. ábra

Sejtésünkre támaszkodva az elég sűrűn felrakott pontokat összekötöttük folytonos ívdarabokkal (4. ábra). Felraktuk

C

-nek a talált

c = 2 a = 2 b

elfajult háromszögből adódó helyzeteit is (

A B

felezőpontja, valamint a fenti

K

L

pontok), ezeken át a pályának az

A B

egyenes két oldalán fekvő részei csatlakoznak egymáshoz. Más egyenesszakasszá elfajult megoldás nincs, mert (8)-ból

c = a + b

helyettesítésével

{(a - b)}^{2} = 0

adódik, amiből

a = b

Fried Ervin‐Bakos Tibor‐Tusnády Gábor