Cím: Az 1966. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, haladók versenye, az általános verseny feladatai
Szerző(k):  Bakos Tibor ,  Lőrincz Pál ,  Surányi János ,  Tusnády Gábor 
Füzet: 1967/május, 200 - 203. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. A és B között vasúti ingajárat közlekedik; a B-be megérkező vonat várakozás nélkül visszaindul A-ba. A vasútvonal mellett kötélpálya is vezet. Egy csille egyszerre indult el A-ból a vonattal. Fél óra múlva a csille ugyanannyira volt A-tól, mint a vonat B-től. A csille további 2km-nyi útja után a két jármű helyzete ismét szimmetrikus lett az AB útszakasz középpontjára nézve. (A vonat közben visszafordult B-ből). Ezután egy negyedóra elteltével a két jármű először találkozott. ‐ Mekkora A és B távolsága és a két jármű sebessége? (Feltesszük, hogy a sebességek állandók.)

 
I. megoldás. Az első fél óra után a vonatnak akkora útja van még hátra B-ig, amennyit a csille megtett ez alatt az idő alatt, együttesen tehát annyi utat tettek meg, mint az AB távolság. A harmadik adat szerinti találkozásig viszont a két jármű együtt oda-vissza bejárta az AB távolságot. Ehhez kétszer annyi idő kellett, tehát a találkozás 1 órával az indulás után történt. A második szimmetrikus helyzet 1/4 órával ezelőtt, vagyis 3/4 órával az indulás után következett be. A csille tehát a mondott 2km-nyi utat az óra harmadik negyedórája alatt tette meg, így sebessége 8km óránként.
Eszerint a csille az első szimmetrikus helyzetben 4km-re, a másikban 6km-re volt A-tól. Ugyanennyire volt a vonat e két időpontban B-től, és mivel közben B-ig ment, és onnan visszafordult, a harmadik negyedóra alatt 10km-t tett meg, sebessége 40km óránként.
Végül A és B távolsága, mint a járművek fél órai útjának összege, 24km.
 
*
 

A versenyzők túlnyomórészt egyenletrendszer felállításával dolgoztak:
 
II. megoldás. A vonat és a csille sebességét (km/óra egységben) v1, ill. v2-vel, az AB távolságot (km-ben) s-sel, a csillének 2km megtételéhez szükséges idejét (órában) t-vel jelölve a feltételek így írhatók fel:

v2⋅12=s-v1⋅12,v2t=2,v2⋅(12+t)=v1⋅(12+t)-s,(v1+v2)(34+t)=2s.



Az első egyenletet átrendezve
v1+v2=2s.
Ezt az utolsó egyenletbe helyettesítve és a 0-tól különböző 2s-sel egyszerűsítve, majd a 2. egyenletet felhasználva
34+t=1,t=14,v2=2t=8.
Ezeket az utolsó két egyenletbe helyettesítve és átrendezve
34(v1-8)=s,v1+8=2s,
és v1-et a második egyenletből az elsőbe helyettesítve
34(2s-16)=s,amibőls=24ésv1=40.

 
Megjegyzés. A gondolatmenet v2 meghatározásáig láthatóan megegyezik az I. megoldáséval.
 
 
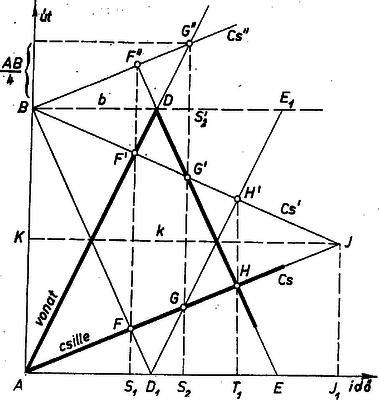1. ábra
 

 
III. megoldás. Mérjük fel egy derékszögű koordinátarendszer tengelyeire a vonat útját (A-tól mérve) és az időt (a közös indulástól számítva, 1. ábra). A vonat mozgását ekkor egy B magasságig egyenesen emelkedő, onnan ugyanolyan szögben süllyedő ADE törött vonal ábrázolja, a DE egyenes az AD egyenes tükörképe az idő-tengellyel B-n át húzott b párhuzamosra. Ezzel lényegében megválasztottuk az idő-tengely és az út-tengely egységeinek arányát, ezért a csille mozgásának grafikonjaként csak egyetlen ACs félegyenes felel meg. Éppen ennek megszerkesztését tekintjük feladatunknak, és kérdéseinkre a választ a helyes grafikonpárból fogjuk kiolvasni.
A járműveknek a pályán mutatkozó szimmetrikus helyzetei a grafikonokban is megmutatkoznak, a grafikonok megfelelő pontjai egymás tükörképei arra a k egyenesre nézve, amely átmegy az AB szakasz K középpontján és párhuzamos az idő-tengellyel. Ezeket a vonat grafikonjából kimetszi ACs-nek k-ra vonatkozó BCs' tükörképe, legyenek ezek rendre F', G', ekkor k-ra való F, G tükörképük ACs-nek ugyanazon abszcisszájú pontja. Másrészt a találkozásnak ACs és a DE grafikonszakasz közös H pontja felel meg. Legyen F, G, H vetülete az idő-tengelyen rendre S1, S2, T1, így az első szimmetrikus helyzetig eltelt fél órának az idő-tengely AS1 szakasza felel meg, a második szimmetrikus helyzettől a találkozásig eltelt negyedórának az S2T1 szakasz. Mármost AS1, S2T1 egyenlő az ABF', illetőleg G'GH háromszögnek az út-tengelyre merőleges magasságával, e két háromszög pedig hasonló, mert az AB, G'G oldalukon levő szögek a végzett tükrözések miatt páronként egyenlők. Eszerint
G'G:AB=S2T1:AS1=14:12,
tehát G'G=AB/2, továbbá G'S'2=S2G=AB/4, ahol S'2 a G' vetülete b-n.
G'-nek b-re vett G'' tükörképe az AD egyenesen van, és itt átmegy BCs'-nek b-re vett BCs'' tükörképe is. Másrészt a kétszeri tükrözés miatt BCs'' előáll ACs-nek azzal az eltolásával is, amely A-t B-be viszi. Ezért GG''=AB, és S2G''=5AB/4=5S2G, ami meghatározza az AD egyenesen G''-t és vele BCs''-t, tehát ACs-t is. Ezek szerint a vonat sebessége 5-ször akkora, mint a csilléé.
Másrészt F'-nek b-re vett tükörképe a DE és BCs'' egyenesek metszéspontja, így FF''=AB=2GG', és az FF''H, GG'H háromszögek hasonló volta miatt S1T1=2⋅S2T1 és S1S2=S2T1, a csillének a két szimmetrikus helyzet közti 2km-es útszakasz megtételéhez ugyancsak 1/4 órára volt szüksége. Eszerint a csille sebessége 8km/ó, a vonaté 40  km/ó. Továbbá AT1 megfelel 1 órának, eddig a vonat és a csille együttes útja 48km, az AB szakasz kétszerese, tehát AB=24km.
Megjegyzés. Az 1. ábrán a vonat‐ csille grafikon-pár meghatározásának az a változata is látható, amelyben az F, G találkozási pontokat ACs-ből ADE-nek BD1E1 tükörképével metsszük ki (vagyis mintha B-ből is indítanánk vonatot A felé). Ekkor BD1∥DE, D1E=BD=AD1, AE=2AD1, és AFD1▵∼AHE▵ miatt AH=2AF, AS1=AT1/2. Másrészt AS1=2S2T és BFF'▵∼G'HH'▵ miatt FF'=2HH' és ACs-nek k-n levő pontját J-vel jelölve FF'J▵∼HH'J▵, így S1J1=2T1J1=S1T1+T1J1, amit a fentebbivel egybevetve AS1=S1T1=T1J1=AJ1/3, és AF=FH=HJ. Ebből a tetszés szerint rajzolt ACs egyenesen kijelölhető F és J helyzete, ami AB=2AK alapján meghatározza BF-et és tükrözéssel AD-t.
 
2. feladat. Adott egy húrnégyszög két átlója, az átlók szöge és a húrnégyszögnek a hosszabb átlóval szemközti egyik szöge. Szerkesztendő a négyszög.
I. megoldás. Legyen ABCD a feltételeket kielégítő négyszög, AC=e≧f=BD az adott hosszúságú átlók, metszéspontjuk M, ABC∢=β, és AMB∢=ω az adott szögek. A betűzés alkalmas választásával feltehetjük, hogy ω≦90∘.
Az adatokból megszerkeszthető a négyszög köré írható k kör, mint olyan kör, amelyiknek egyik ívéről az e szakasz β szögben látszik. Ezután f hosszúságú húrt kell elhelyeznünk úgy, hogy az az e hosszúságú húrt ω szögben messe.
A k kör f hosszúságú húrjai felezőpontjukban érintenek egy k-val koncentrikus k' kört. Ehhez kell AC-vel ω szöget bezáró érintőt szerkeszteni.
 
 
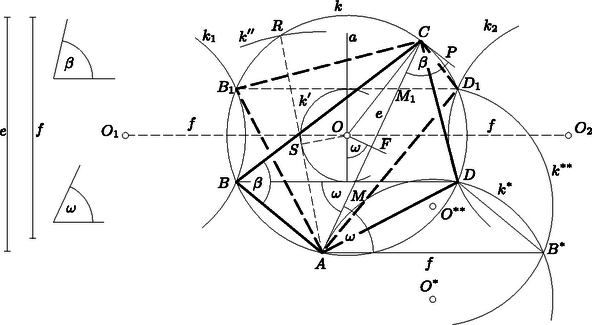2. ábra
 

Ezek alapján a szerkesztés pl. a következő módon végezhető: AC=e hosszúságú szakaszt rajzolunk, és erre ACP∢=β szöget szerkesztünk; a CP-re C-ben szerkesztett merőlegesnek és az AC-re F felezőpontjában állított merőlegesnek O metszéspontja körül C-n át szerkesztett k kör a négyszög köré írt kör. Ezt pl. A-ból f sugarú körrel egyik irányban elmetsszük az R pontban.
Az AR-re O-bó1 bocsátott merőleges S talppontján át O körül húzott kör k'. Szerkesszük meg O-n át azt az a egyenest, amelyik AC felező merőlegesének AC felé haladó félegyenesével az egyenes A-t tartalmazó partján ω szöget zár be. Ennek k'-vel való metszéspontjaiban k'-höz húzott érintők (a-ra állított merőlegesek) k-ba eső húrjai f hosszúságúak és egyenesük AC-vel ω szöget zár be, mert e hajlásszög szárai a-ra, ill. OF-re merőlegesek.
Ahhoz, hogy az A és C pont és a most szerkesztett valamelyik húr végpontjai meghatározta négyszögben az e és f hosszúságú húr átló legyen, kell, hogy a kettő messe egymást. Ha ez teljesül, akkor jelöljük D-vel az f hosszúságú húrnak azt a végpontját, amelyik az AC egyenesnek ugyanazon a partján van, mint P, a másik végpontot B-vel. Így a kerületi szögek egyenlősége folytán ABC∢=ACP∢=β, ugyanis CP a k kör érintője, mert szerkesztés szerint merőleges az OC sugárra. Ezek szerint az ABCD négyszög megfelel a feladat követelményeinek.
Mindig megszerkeszthető a k kör és e≧f folytán az AR húr, a k' kör, az a egyenes és erre a k'-vel való metszéspontjaiban állított merőlegesek. A feladatnak nincs megoldása, 1 vagy 2 megoldása van aszerint, hogy az a-ra állított merőlegesek k-ba eső szakaszai nem metszik AC-t, ill. csak az egyikük, vagy mind a kettő metszi.
 
Megjegyzés. A k kör f hosszúságú, kívánt állású húrjainak végpontjait kimetszhetjük azokkal a k1, k2 körökkel is, amelyek k-nak f nagyságú eltolásával adódnak az e-vel ω szöget bezáró (és egymással ellentétes) irányban. f≦e miatt közös pont mindig van, és a húr megfelel, ha végpontjai AC két oldalán adódnak.
 
II. megoldás. Tovább is a fenti jelöléseket használjuk. Tükrözzük az AD oldal E felezőpontjára* B-t, O-t és k-t, legyen a kép B*, 0*, k*. Ekkor egyrészt ABDB* paralelogramma, AB*#BD, és B*AM∢=BMA∢=ω, váltószögek, mert E, és így B* is AC-nek B-t nem tartalmazó partján van, M pedig az AC szakaszon. Másrészt D a k és k* metszéspontja. Így a következő szerkesztéshez jutottunk.
AC-nek, O-nak és k-nak a fentiek szerinti megszerkesztése után felmérjük a CAB*∢=ω szöget, és új szárára az AB*=f szakaszt. AB* mint húr fölé OC sugarú k* kört szerkesztünk, ennek k-val való metszéspontja D, végül B* tükörképe AD felezőpontjára nézve B.
A kapott ABCD négyszögben AC=e, BD=AB*=f és BMA∢=MAB*∢=ω, továbbá k átmegy B-n, mert k és k*, mint egyenlő sugarú körök, egymás tükörképei a közös AD húrjuk felezőpontjára nézve, tehát a feltétel alapján ABC∢=β.
B* egyértelműen szerkeszthető és D létrejön, mert k-nak és k*-nak van közös pontja: A.
k* helyett AB*-ra való k** tükörképét használva újabb megoldást kapunk. A megoldások megfelelnek, ha D az AC egyenes B*-ot tartalmazó partján adódik, számuk legfeljebb 2.
 
3. feladat. Alakítsuk két polinom szorzatává az
x4+x3+x2+x+1
kifejezést.
 
I. megoldás. Olyan felbontást keresünk, melyben mindkét tényező-polinom másodfokú és x2 együtthatója mindkettőben 1. Feladatunk a további p, q, illetőleg r, s együtthatók meghatározása úgy, hogy

(x2+px+q)⋅(x2+rx+s)=x4+(p+r)x3+(q+pr+s)x2+(qr+ps)x+qs==x4+x3+x2+x+1.



azonosság legyen. Ez teljesül, ha x3, x2, x együtthatója és az x-et nem tartalmazó tag a két oldalon rendre egyenlő, azaz, ha
(1)p+r=1,(2)q+pr+s=1,(3)qr+ps=1,(4)qs=1.

(3)-at q-val megszorozva, (1) és (4) felhasználásával kiküszöbölhetjük r-et és s-et. (1)-ből r=1-p, így

q2r+qps=q2(1-p)+p=q,q2-q-p(q2-1)=(q-1)(q-pq-p)=0.(5)



Ez mindenesetre teljesül, ha q=1, amikor (4)-ből s=1, (2)-ből pr=-1, és (1)-et is tekintetbe véve p és r a
(z-p)(z-r)=z2-(p+r)z+pr=z2-z-1=0(6)
egyenlet gyökei, tehát az (1+5)/2 és (1-5)/2 értékek. Ezekkel fennáll a
P(x)=x4+x3+x2+x+1=(x2+1+52x+1)(x2-5-12x+1)
azonosság. Ezzel megkaptunk egy kívánt alakú felbontást.
 
Megjegyzések. 1. Egy első és egy harmadfokú, valós együtthatós tényezőre való felbontás nem létezik, mert különben volna P(x)-nek valós 0-helye, de az a talált felbontás valamelyik tényezőjének is 0-helye volna. Ámde mindkét tényező diszkriminánsa negatív, s így egyiknek sincs valós 0-helye.
2. Világos, hogy q=1 választás mellett a föntin kívül csak olyan, két másodfokú valós együtthatós tényezőből álló felbontás nyerhető, amelyik abból az egyik tényezőnek egy 0-tól különböző c számmal, a másiknak 1/c-vel való szorzásával keletkezik. Ha viszont a q-pq-p=0 egyenletből indulunk ki, akkor (2)-ből pl. p-re negyedfokú egyenletet nyerünk, ami teljes négyzetté kiegészítésén keresztül másodfokú tényezőkre bontható, de azok egyikének sincs valós 0-helye. Így nincs a fentitől lényegesen különböző, valós együtthatós felbontás másodfokú tényezőkre sem.
 
II. megoldás. A polinomot x2+1 hatványai szerint rendezhetjük:
P(x)=x4+1+x(x2+1)+x2=(x2+1)2+x(x2+1)-x2.
Egészítsük ki az első két tagot teljes négyzetté, így két négyzet különbsége keletkezik, amit már szorzattá alakíthatunk:
P(x)=(x2+1+12x)2-54x2=(x2+1+52x+1)⋅(x2+1-52x+1).

Megjegyzések. 1. Az eljárás általában alkalmazható x4+ax3+bx2+ax+1 alakú, ún. szimmetrikus polinomokra, és nem különbözik lényegesen attól a szokásos eljárástól, amely szerint a polinom 1/x2-szeresét az y=x+1x új változóval fejezzük ki.
Az itt vázolt úton mindig eljutunk két, valós együtthatós másodfokú tényezőre bontáshoz, ha a2-4b+8≧0.
2. Az I. megoldás gondolatmenete is alkalmazható az említett általánosabb esetben, és célra vezet, bármilyen értékek is az együtthatók.
 
Lőrincz Pál‐Bakos Tibor‐Tusnády Gábor‐Surányi János
*Az ábrán E pótlandó.