Cím:	1966. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):	Hajós György
Füzet:	1967/május, 193 - 200. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1966. évi Kürschák József matematikai tanulóverseny feladatainak megoldása   Első feladat. Van-e olyan térbeli ötszög, amelynek oldalai egyenlők, és bármely két szomszédos oldala derékszöget alkot?   I. megoldás. A feladat követelményeit kielégítő $ABCDE$ ötszög keresésekor nyilván közömbös, hogy az oldalhosszat mekkorának választjuk. Kiindulhatunk ezért az egységoldalú $ABCO$ négyzetből, s azt vizsgáljuk, hogy a $D$, $E$ csúcsok hol helyezkedhetnek el. Minthogy $BCD\sphericalangle ={90}^{\circ }$ és $CD=1$, a $D$ pont abban a $\gamma$ síkban van, amely a $BC$ egyenest $C$-ben merőlegesen metszi, mégpedig e sík $C$ középpontú, $CO$ sugarú körén helyezkedik el (1. ábra). A keresett ötszög átlói egyenlők, hiszen mindegyik egy-egy egységbefogójú egyenlőszárú derékszögű háromszög átfogója (közös hosszuk $\sqrt[]{2}$ ). Eszerint $AD=AC$, s így a $D$ pont rajta van a $\gamma$ sík $O$ középpontú, $OC$ sugarú körén is, hiszen a $\gamma$ síkban ez a kör azoknak a pontoknak a mértani helye, amelyek $A$-tól $AC$ távolságra vannak. A $D$ pont ezek szerint csak a mondott két kör valamelyik metszéspontja lehet. Az egyik metszéspontot önkényesen kijelölhetjük $D$ helyzetéül, hiszen a két metszéspont az $ABC$ síkra vonatkozólag szimmetrikusan helyezkedik el, s a keresett ötszöget is tükrözhetjük erre a síkra. $D$ helyzetéhez a legegyszerűbben úgy jutunk, hogy a $CO$ szakaszhoz a $\gamma$ síkban valamelyik oldalról egy szabályos háromszöget illesztünk, s ennek harmadik csúcsát tekintjük. 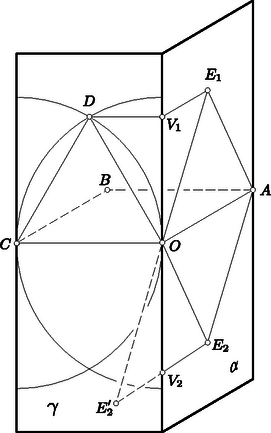    1. ábra   Ugyanígy okoskodhatunk az $E$ pont helyzetét illetően is. Az adódik tehát, hogy ha a $BA$ szakaszra $A$-ban merőlegesen emelt $\alpha$ síkban az $OA$ szakaszhoz mindkét oldalról egy-egy szabályos háromszöget illesztünk, s ezek harmadik csúcsát $E_1$ és $E_2$ jelöli, akkor $E$ csak ezek valamelyike lehet. Itt már mind a két lehetőségre gondolnunk kell, mert az $ABC$ síkra vonatkozó tükrözés lehetősége $D$ megválasztása után már nem áll fenn. Bebizonyítjuk, hogy nincs kívánt tulajdonságú ötszög, mégpedig azért nincs, mert a $D{E}_1$ és $D{E}_2$ távolságok egyike sem egységnyi. Erről számítással könnyen meggyőződhetünk. Jelölje $V_1$ az $E_1$ pontnak a $\gamma$ síkra vetett merőleges vetületét. A derékszögű $D{V}_1{E}_1$ és $D{E}_1{E}_2$ háromszögek befogóira $D{V}_1=V_1{E}_1=\frac{1}{2}$ és $E_1{E}_2=\sqrt[]{3}$. Így tehát Pythagoras tétele szerint ${\displaystyle \begin{array}{c}\hfill {\displaystyle D{E}_1=\sqrt[]{\frac{1}{4}+\frac{1}{4}}=\frac{1}{\sqrt[]{2}}<\mathrm{1,}}\hfill \\ \hfill {\displaystyle D{E}_2=\sqrt[]{\frac{1}{2}+3}=\sqrt[]{\frac{7}{2}}>1.}\hfill \end{array}}$ A feladat kérdésére tehát valóban nemmel kell felelni.   Megjegyzések. Megoldásunkat többféleképpen is befejezhettük volna. Három ilyen lehetőséget említünk. 1. Az utolsó lépést kevesebb számolással is elintézhetjük. Evégett bevezetjük az $E_2$ pont $\gamma$ síkra vonatkozó $E{\text{'}}_2$ tükörképét, amely egyben $E_1$ tükörképe az $O$ pontra vonatkozólag. A $D{V}_1{E}_1$ és $DE{\text{'}}_2{E}_1$ háromszögekre vonatkozó háromszög-egyenlőtlenségeket felhasználva ${\displaystyle \begin{array}{c}\hfill {\displaystyle D{E}_1<D{V}_1+V_1{E}_1=\frac{1}{2}+\frac{1}{2}=\mathrm{1,}}\hfill \\ \hfill {\displaystyle D{E}_2=DE{\text{'}}_2>E{\text{'}}_2{E}_1-D{E}_1=2-D{E}_1>1.}\hfill \end{array}}$ A második becslésnél az első eredményét is felhasználtuk. 2. A $D{E}_1<1$, $D{E}_2>1$ egyenlőtlenségek nyomban adódnak abból, hogy $DO{E}_1\sphericalangle <{60}^{\circ }$ és $DO{E}_2\sphericalangle >{60}^{\circ }$. Elég az első helyességét belátnunk, hiszen $DO{E}_2\sphericalangle =DOE{\text{'}}_2\sphericalangle$ és ez a $DO{E}_1\sphericalangle$ kiegészítő szöge, tehát az első egyenlőtlenség szerint ${120}^{\circ }$-nál is nagyobb. Az első egyenlőtlenség viszont a triéder oldalaira vonatkozó egyenlőtlenségből adódik, amely szerint $\begin{array}{c}{\displaystyle DO{E}_1\sphericalangle <DO{V}_1\sphericalangle +V_{1}O{E}_1\sphericalangle ={30}^{\circ }+{30}^{\circ }={60}^{\circ }\mathrm{.}}\end{array}$ 3. Az adódott lehetőségek meg nem felelő volta abból is következik, hogy a $D{E}_1$ és $D{E}_2$ szakaszok egyike sem merőleges $CD$-re, vagyis abból, hogy az $E_1$, $E_2$ pontok egyike sincs a $DC$-re $D$-ben merőlegesen emelt síkban. Ez a sík ugyanis merőleges $\gamma$-ra, tehát tartalmazza minden pontjának $\gamma$-ra vetett merőleges vetületét. Ez $E_1$ és $E_2$ esetében azt jelentené, hogy a $CD{V}_1\sphericalangle$ és $CD{V}_2\sphericalangle$ valamelyike derékszög (itt $V_2$ az $E_2$ pont vetületét jelöli), márpedig az első ${120}^{\circ }$, a második pedig ${60}^{\circ }$-nál kisebb, hiszen része a $CDO\sphericalangle$-nek.   II. megoldás. Azt állítjuk, hogy a követelményeket kielégítő ötszög átlóinak felezőpontjai egymástól mindannyian ugyanakkora távolságra vannak. Két ugyanabból a csúcsból kiinduló átló felezőpontjának távolsága az átlók által kifeszített háromszög középvonala, tehát a harmadik oldalnak, ötszögünk egy oldalának a fele. Egymáshoz nem csatlakozó átlók esetében első megoldásunknak arra a megállapítására támaszkodunk, hogy a $D$ pont az $ABCO$ négyzethez csatlakozó szabályos $CDO\Delta$ csúcsa. Az $AC$, $BD$ átlók felezőpontjának távolságát keressük. Minthogy az $AC$, $BO$ szakaszok felezőpontja azonos, a $BO$, $BD$ szakaszok felezőpontjának távolságát kell meghatároznunk. Ez azonban a $BOD\Delta$ középvonala, s így az $OD$ távolság fele, tehát szintén ötszögünk oldalának felével egyenlő. Ezek szerint, ha van a feladat követelményeit kielégítő ötszög, akkor van a térben öt olyan pont, amelyek páronként egymástól ugyanakkora távolságra vannak. Minthogy azonban nincs öt ilyen pont, a feladat követelményeit kielégítő ötszög sincs. Egymástól páronként ugyanakkora távolságra levő öt pont valóban nem létezik, mert közülük négy egy szabályos tetraédert határoz meg, s az ötödik, a tetraéder valamennyi csúcsától egyenlő távolságra elhelyezkedő pont csak a tetraéder köré írt gömb középpontja lehetne, de ennek a gömbnek a sugara a tetraéder élénél kisebb. (Ez a megoldás Kárteszi Ferenctől való.)   Megjegyzések. Első megoldásunk többféle befejezési lehetősége azt sejtetheti, hogy a feladat követelményeinek megfelelő lazítása után is nemmel kell a feladat kérdésére válaszolni. Megvizsgáljuk ezért, hogy különféle lazítások esetén mi a válasz. 1. Ha csak azt követeljük meg, hogy a térbeli ötszög oldalai közül négy legyen egyenlő, viszont minden szöge derékszög legyen, akkor már található a követelményt kielégítő ötszög. Ezt a 2. ábra példája mutatja, ahol az ötszög csúcsai egy kocka csúcsai közül valók. Ugyanígy található ötszög, ha az oldalak egyenlőségén kívül csak azt követeljük meg, hogy a szögek közül négy derékszög legyen. Ezt a 3. ábra mutatja, amely egy csupa egyenlő éllel rendelkező, szabályos háromoldalú hasáb éleiből alkotott ötszöget mutat be. 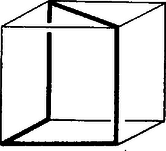    2. ábra 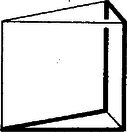      3. ábra   2. Igennel kell a feladat kérdésére válaszolni akkor is, ha a követelményeken mit sem enyhítünk, viszont öt helyett többoldalú sokszöget keresünk. Hat és nyolcoldalút könnyen alkothatunk egy kocka éleiből. Hétoldalúhoz jutunk, ha olyan szimmetrikus trapézből indulunk ki, amelynek szárai és egyik alapja egységnyiek, másik alapjának hossza pedig $\sqrt[]{2}$, majd ehhez egy egyenlőszárú derékszögű háromszöget, az egységnyi hosszúságú alaphoz pedig egy négyzetet illesztünk. Ha ezt a négyzetet a trapéz síkjára merőlegesen felhajtjuk, az egyenlőszárú derékszögű háromszöget pedig annyira hajtjuk fel, hogy befogói a trapézszárakra merőlegesek legyenek, akkor kívánt tulajdonságú hétszöghöz jutottunk el. Nyolcnál nagyobb oldalszámú ilyen sokszöget már könnyen találhatunk. 3. Ha olyan ötszöget keresünk, amelynek oldalai egyenlők, és bármely két szomszédos oldala ugyanakkora szöget alkot, nem követelve meg, hogy ez a szög derékszög legyen, akkor már nem felelhetünk a feladat kérdésére egyszerűen igennel vagy nemmel. Következő megoldásunk erre a kérdésre is válaszol.   III. megoldás. Felhasználjuk azt, hogy ha az $A$, $B$, $C$, $D$, $E$ pontok távolságai rendre egyenlők az $A_1$, $B_1$, $C_1$, $D_1$, $E_1$ pontok megfelelő távolságaival, akkor van olyan egybevágóság, amely az első pontötöst a másodikba viszi át. Ez öt helyett akárhány pontra is igaz, de mi csak öt pontra alkalmazzuk. Azt vizsgáljuk, hogy melyek azok az ötszögek, amelyeknek oldalai egyenlők, és bármely két szomszédos oldaluk ugyanakkora szöget alkot. Bebizonyítjuk, hogy csak a síkbeli szabályos ötszög és az ennek átlóiból alakított szabályos csillagötszög ilyen, ahol is az egyenlő szögek nagysága ${108}^{\circ }$, illetve ${36}^{\circ }$. Bebizonyítjuk tehát azt is, hogy a feladat eredeti kérdésére nemmel kell válaszolni. A bizonyításhoz abból indulunk ki, hogy az egyenlőoldalú és egyenlőszögű $ABCDE$ ötszög átlói egyenlők, hiszen mindegyik egy-egy olyan egyenlőszárú háromszög alapja, amelynek szára és szárszöge az ötszög oldala és szöge. Az előrebocsátottak szerint van tehát olyan egybevágóság, amely az $ABCDE$ ötszöget a $BCDEA$ ötszögre helyezi, s ugyanezt az öt csúcs minden ciklikus permutációjáról is elmondhatjuk. Ezek az egybevágóságok az öt pont konvex burkát is önmagára helyezik, s mivel van közöttük olyan, amely csúcsa a konvex buroknak, a ciklikus permutáció szabad megválaszthatósága miatt mind az öt pont ilyen. Ha az öt pont nincs egy síkban, akkor a konvex burkuk ötcsúcsú poliéder, tehát csak négyoldalú gúla vagy háromoldalú kettősgúla (két közös lapú tetraéder egyesítése) lehet. Mindkettőnek van háromélű csúcsa és négyélű csúcsa is. Minthogy azonban háromélű csúcsot egybevágóság nem vihet át négyélű csúcsba, ellentmondásra jutottunk. Ha tehát az ötszög nem síkbeli, akkor nem lehet minden oldala és minden szöge egyenlő. Ha az öt pont egy síkban van, akkor konvex burkuk a fentiek szerint olyan ötszög, amelynek csúcsai egybevágósággal szabadon permutálhatók. Az öt pont konvex burka ezért csak szabályos ötszög lehet, s a keresett egyenlőoldalú és egyenlőszögű ötszöget vagy a szabályos ötszög oldalai, vagy annak átlói alkotják.   Második feladat. Bizonyítsuk be, hogy ha $n$ természetes szám, akkor $\begin{array}{c}{\displaystyle {\left(5+\sqrt[]{26}\right)}^n}\end{array}$ tizedestört alakjában a tizedesvesszőt követő első $n$ jegy egyenlő.   Megoldás. Bebizonyítjuk, hogy a tizedesvesszőt követő első $n$ jegy $0$ vagy $9$-es, hogy tehát a vizsgált szám egy egész számtól ${10}^{-n}$-nél kevesebbel tér el. Ehhez elég belátni, hogy $\begin{array}{c}{\displaystyle {\left(5+\sqrt[]{26}\right)}^n+{\left(5-\sqrt[]{26}\right)}^n}\end{array}$ egész szám, s hogy $\begin{array}{c}{\displaystyle \left|5-\sqrt[]{26}\right|<\frac{1}{10}\mathrm{.}}\end{array}$ Az utóbbi számítással könnyen ellenőrizhető, de abból is adódik, hogy $5\mathrm{,}{1}^2=26\mathrm{,}01>26$, s ezért $\begin{array}{c}{\displaystyle 5<\sqrt[]{26}<5\mathrm{,}1.}\end{array}$ A még bebizonyítandó állítás $p\left(x\right)={\left(5+x\right)}^n$ jelöléssel azt mondja ki, hogy $p\left(\sqrt[]{26}\right)+p\left(-\sqrt[]{26}\right)$ egész szám. Ez valóban igaz, mert ha a $p\left(x\right)$ polinomban $x$ helyébe $\left(-x\right)$-et írunk, az $x$ páratlan kitevős hatványait tartalmazó tagok előjele megváltozik, s ezért az egész együtthatós $p\left(x\right)+p\left(-x\right)$ polinomban csak $x$ páros kitevőjű hatványai szerepelnek. Így tehát e polinom értéke az $x=\sqrt[]{26}$ helyen valóban egész szám. Minthogy $5-\sqrt[]{26}$ negatív, megoldásunk azt is mutatja, hogy páratlan $n$ esetén a tizedesvesszőt követő első $n$ jegy $0$, páros $n$ esetén pedig $9$-es.   Megjegyzések. 1. Nem volt szükségünk a binomiális tételre, bár megtehettük volna, hogy a $p\left(x\right)$ polinom együtthatóit a binomiális tétel segítségével fel is írjuk. 2. Megoldásunkból könnyen kiolvasható, hogy ha $n$ elég nagy, akkor a tizedesvesszőt $n$-nél több egyenlő jegy követi. Megemlítjük, hogy ez első ízben az $n=234$ kitevőre következik be.   Harmadik feladat. Van-e nem-negatív egész számokból álló olyan két végtelen $A$ és $B$ halmaz, hogy bármely nem-negatív egész szám pontosan egyféleképpen írható fel egy $A$-hoz tartozó és egy $B$-hez tartozó szám összegeként?   Megoldás. Megmutatjuk, hogy vannak kívánt tulajdonságú $A$, $B$ számhalmazok, s ehhez elég egyetlenegy példát megadnunk. Tartozzanak az $A$ halmazhoz mindazok a nem-negatív egész számok, amelyeknek minden $0$-tól különböző tizedesjegye (a szám végétől visszafelé számítva) páratlanadik helyen áll, $B$-hez pedig azok, amelyeknek minden $0$-tól különböző jegye párosadik helyen helyezkedik el. A $0$ eszerint mind a két halmazhoz hozzátartozik, hiszen nincs $0$-tól különböző tizedesjegye. Ha egy-egy $A$-hoz és $B$-hez tartozó számot összeadunk, akkor az összeg tizedesjegyei éppen a két szám megfelelő tizedesjegyei lesznek, hiszen ugyanazon a helyen mindig csak az egyikben állhat $0$-tól különböző számjegy, s ez lesz az összeg tizedesjegye. Bármely nem-negatív egész szám páratlanadik jegyeiből egy $A$-hoz, párosadik jegyeiből egy B-hez tartozó számot alkothatunk, s ezek összege a fentiek szerint éppen az a szám lesz, amelyből kiindultunk. A két halmaz más számainak összege nem lehet ugyanez az érték, mert valahol más tizedesjegynek kell bennük szerepelnie, s akkor ezt összegük is tartalmazza. Ha pl. $1967$-ből indulunk ki, akkor ebből az $A$-hoz tartozó $907$ és a $B$-hez tartozó $1060$ adódik. Ezek összege valóban $1967$. Meg kell még állapítanunk, hogy az $A$, $B$ halmazok mindegyike végtelen halmaz. Ez igaz, mert végtelen sok páratlanadik és végtelen sok párosadik tizedeshely van.   Megjegyzések. 1. A feladat megoldásaként csak egyetlenegy példát adtunk meg. Sok más példát is megadhattunk volna. Eljárásunk változatlanul alkalmazható, ha nem tízes, hanem tetszőleges alapú számrendszert használunk. Legtetszetősebbnek talán a kettes számrendszer választásakor adódó példa mondható. Megoldásunkban a (szám végétől visszafelé számlált) páratlanadik és párosadik tizedeshelyek szolgáltatták a két számhalmazt. Ehelyett a tizedeshelyeket akárhogyan is eloszthattuk volna két csoportba, mindenesetre azonban úgy, hogy mindkét csoport végtelen sok tizedeshelyet tartalmazzon. Így pl. sorolhatnók az egyikbe azokat a tizedeshelyeket, amelyeknek a szám végétől visszafelé számított sorszáma $3$-mal osztható, s a másikba a többit. Vagy az egyikbe azokat, amelyeknek a sorszáma törzsszám, s a másikba a többit. Ilyen módon újabb példákhoz juthatunk természetesen akkor is, ha nem a tízes számrendszert használjuk. További példákhoz jutunk, ha változó alapú számrendszerből indulunk ki. Ez a következőt jelenti: tetszőlegesen megválasztjuk az $1$-nél nagyobb $k_1$, $k_2\mathrm{,}\text{...}$ alapszámokat; ezekkel minden nem-negatív egész számot kifejezhetünk $\begin{array}{c}{\displaystyle c_1+c_2{k}_1+c_3{k}_1{k}_2+c_4{k}_1{k}_2{k}_3+\text{...}}\end{array}$ alakban, ahol a $c_1$, $c_2\mathrm{,}\text{...}$ számjegyek mindegyikére teljesül a $0\le c_i<k_i$ megszorítás, és természetesen minden szám kifejezésében csak véges sok számjegy szerepel. Egy szám számjegyeihez úgy juthatunk el, hogy azt $k_1$-gyel osztva $c_1$ lesz a maradék, a hányadost $k_2$-vel osztva maradékként $c_2$ adódik, majd a hányadosokat mindig tovább osztva a többi számjegyet is megkapjuk. Ilyen változó alapú számrendszerre változatlanul alkalmazhatjuk megoldásunk eredeti eljárását, s így a feladat kérdésére adott válasz helyességét bizonyító újabb példákat kapunk. Könnyen meggyőződhetünk arról, hogy minden korábban említett példa ennek a most ismertetett példának speciális esete. 2. Megmutatjuk, hogy a most megismert példa a legáltalánosabb, hogy tehát a feladat követelményét kielégítő bármely $A$, $B$ halmazpárhoz el lehet jutni a változó alapú számrendszer alapszámainak megfelelő megválasztása után megoldásunk eredeti módszerével. Legyen tehát $A$ és $B$ a feladat követelményét kielégítő két számhalmaz. Eszerint minden nem-negatív egész szám pontosan egyféleképpen állítható elő $A$ és $B$ egy-egy elemének összegeként. Ha a következőkben előállításról szólunk, mindig ilyen előállításra gondolunk. Jelölje $a\left(n\right)$ és $b\left(n\right)$ a két halmaznak azt az elemét, amelyek $n$ előállításában fellépnek, amelyekre tehát $n=a\left(n\right)+b\left(n\right)$. A $0$ mindkét halmaz eleme, mert különben $0$ nem volna a két halmaz egy-egy elemének összegeként előállítható. A két halmaznak nincs más közös eleme, mert ha $n$ ilyen volna, akkor $n$ kétféleképpen is előállítható volna, ti. $n+0$ és $0+n$ alakban. Valamelyik halmaz elemei között $1$ is szerepel, mert különben $1$ nem volna előállítható. Legyen $A$ ez a halmaz, s legyen $k_1$ az a legkisebb természetes szám, amely $A$-nak nem eleme. Azt állítjuk, hogy $k_1$ szerepel $B$-ben. $b\left(k_1\right)$ nem lehet $0$, mert ebből $a\left(k_1\right)=k_1$ következnék, pedig $k_1$ nem tartozik $A$-hoz. Nem lehet $b\left(k_1\right)$ az $1$, $\mathrm{2,}\text{...}\mathrm{,}{k}_1-1$ számok egyikével sem egyenlő, mert mindezek $A$ elemei. Ezért szükségképpen $b\left(k_1\right)=k_1$, tehát $k_1$ valóban eleme a $B$ halmaznak. A nem-negatív egész számokat $k_1$ számból álló ,,szakaszokba'' osztjuk be. Egy ilyen szakasz a $\begin{array}{c}{\displaystyle t{k}_1\mathrm{,}t{k}_1+\mathrm{1,}\text{...}\mathrm{,}t{k}_1+\left(k_1-1\right)}\end{array}$ (*) számokból áll. Azt állítjuk, hogy egy-egy ilyen szakasz $x$ számaira $b\left(x\right)$ értéke azonos, s hogy ez az érték $k_1$ többszöröse. Ez persze azt is jelenti, hogy a szakasz számaihoz tartozó $a\left(x\right)$ értékek ugyancsak egy teljes szakaszt alkotnak. Állításunkat $t$-re vonatkozó teljes indukcióval bizonyítjuk be. Az állítás a $t=0$ értékre teljesül, hiszen a kezdőszakasz minden elemére $b\left(x\right)=0$. Feltesszük, hogy állításunk a $t{k}_1$ számot megelőző szakaszok mindegyikére helyes, bebizonyítjuk, hogy helyes a (*) szakaszra is. Feltevésünkből következik, hogy az $A$ halmaz $t{k}_1$-nél kisebb elemei teljes szakaszokat alkotnak, hiszen $A$ minden eleme fellép saját magának az előállításában, hozzá $B$-ből a $0$ elemet adva, s akkor a tartalmazó szakasz minden elemére $b\left(x\right)=0$, a megfelelő $a\left(x\right)=x$ értékek tehát valóban egy teljes szakaszt alkotnak. Feltevésünkből az is következik, hogy a $B$ halmaz $t{k}_1$-nél kisebb elemei mindannyian $k_1$ többszörösei, hiszen mindegyik fellép a saját előállításában ($A$-ból a $0$ elemet adva hozzá), s azért az indukciós feltevés reá is vonatkozik. Tekintsük most már a (*) szakasz számainak előállítását. Ha e szakasz valamelyik $x$ elemére $a\left(x\right)<t{k}_1$ és $b\left(x\right)<t{k}_1$, akkor utolsó megállapításunk szerint $b\left(x\right)$ osztható $k_1$-gyel, s így az $a\left(x\right)+b\left(x\right)$ összegben $a\left(x\right)$ helyébe az ezt az értéket tartalmazó és $A$-hoz tartozó szakasz elemeit írva a (*) szakasz minden elemének előállításához eljutunk. Ilyenkor tehát a bizonyítandó állítás teljesül. Azt az esetet kell már csak vizsgálnunk, amikor (*) minden elemének előállításában szerepel $t{k}_1$-nél nem kisebb szám is. Maga $t{k}_1$ tehát vagy $t{k}_1+0$, vagy $0+t{k}_1$ módon állítható elő. Az utóbbi esetben $0$ helyébe az $A$-hoz tartozó $1$, $\mathrm{2,}\text{...}\mathrm{,}{k}_1-1$ számokat írva ismét eljutunk (*) minden elemének olyan előállításához, amelyre állításunk teljesül. Legyen tehát $a\left(t{k}_1\right)=t{k}_1$. Ekkor $t{k}_1$ az $A$ halmaz eleme. A (*) szakasz többi eleme sem tartozhatik $B$-hez, mert ha $t{k}_1+c_1$ odatartoznék, ahol $0<c_1<k_1$, akkor $\begin{array}{c}{\displaystyle \left(k_1-c_1\right)+\left(t{k}_1+c_1\right)=t{k}_1+k_1}\end{array}$ ugyanannak a számnak kétféle előállítása volna. Eszerint a (*) szakasz $x$ elemére $b\left(x\right)\ge t{k}_1$ nem teljesülhet, s ezért a vizsgált eset tulajdonsága miatt szükségképpen $a\left(x\right)\ge t{k}_1$, amiből $x<t{k}_1+k_1$ miatt $b\left(x\right)<k_1$ következik. Minthogy azonban $B$ a $k_1$-nél kisebb számok közül csak a $0$-t tartalmazza, a $b\left(x\right)=0$ eredményhez jutunk (amiből az is következik, hogy a teljes (*) szakasz $A$-hoz tartozik). Eszerint a bizonyítandó állítás most is teljesül. Indukciós okoskodásunk befejezése után megállapíthatjuk, hogy az $A$ halmaz teljes ,,szakaszokból'' áll, s hogy $B$ minden eleme $k_1$ többszöröse. Mindkét halmaz teljes ismeretéhez elég eszerint azt tudnunk, hogy $k_1$ többszörösei közül melyeket tartalmazzák. Tekintsünk olyan változó alapú számrendszert, amelynek első alapszáma $k_1$. Eredményünk szerint ebben a számrendszerben $B$ minden elemének első jegye $0$, viszont $A$ bármely elemének első jegyét tetszőlegesen megváltoztatva megint $A$ eleméhez jutunk. Azt vizsgáljuk, hogy $k_1$ többszörösei közül melyek tartoznak a két halmazhoz. Álljon az $A_1$ halmaz azokból a nem-negatív $n$ egész számokból, amelyekre $n{k}_1$ az $A$ halmaz eleme, $B_1$ pedig azokból, amelyekre $n{k}_1$ a $B$ halmaz eleme. Az $A_1$, $B_1$ halmazok rendelkeznek az $A$, $B$ halmazoknak a feladatban foglalt tulajdonságaival, hiszen $k_1$ többszörösei is egyféleképpen állíthatók elő és előállításukban a fentiek szerint csak $k_1$ többszörösei lépnek fel. Különbség van azonban $A$ és $B$, valamint $A_1$ és $B_1$ szereposztásában, mert mintegy szerepet cserélnek. Azt a halmazt jelöltük $A$-val, amelynek $1$ eleme, most viszont $B_1$ játssza ezt a szerepet, hiszen $1$ ennek eleme, mert $k_1$ a $B$ halmazhoz tartozik. Az $A_1$, $B_1$ halmazokra elvégezhetjük ugyanazt az okoskodást, amelyet az $A$, $B$ halmazokra már elvégeztünk. Ezt azzal kezdjük, hogy a legkisebb, $B_1$ hez nem tartozó természetes számot $k_2$-vel jelöljük. Így azt kapjuk, hogy $A_1$ minden eleme $k_2$ többszöröse, $B_1$ pedig $k_2$ számból álló teljes ,,szakaszokból'' áll. Ha $k_2$-t választjuk számrendszerünk második alapszámául, akkor tehát elmondhatjuk, hogy $A$ minden elemének második jegye $0$, viszont $B$ minden elemének második jegyét szabadon megváltoztathatjuk, s megint $B$ eleméhez jutunk. Ezt az eljárást minden határon túl folytathatjuk, hiszen végtelen halmazokból indultunk ki. Eljutunk tehát egy változó alapú számrendszer $k_1$, $k_2\text{...}$ alapszámainak végtelen sorozatához. Minthogy a növekvő indexű halmazok állandóan szerepet cserélnek, ahhoz az eredményhez jutunk, hogy $A$ elemeinek minden párosadik jegye $0$, páratlanadik jegyeik pedig tetszőlegesek, a $B$ halmaz elemeinél viszont fordítva, minden páratlanadik jegyük $0$, és párosadik jegyeik tetszőlegesek. Megoldásunk eredeti módszere tehát valóban ehhez a két halmazhoz vezet el, ha az előírásunknak megfelelő változó alapú számrendszert használjuk. 3. A feladat két általánosítását említjük még meg. A részletek kidolgozását azonban már az olvasóra bízzuk. A feladat kérdésére igennel kell felelni akkor is, ha nem két végtelen halmazról, hanem kettőnél többről van a feladatban szó. Ez első megjegyzésünknek ahhoz az észrevételéhez kapcsolódik, hogy a tizedeshelyeket akárhogyan beoszthatjuk két (végtelen sok tizedeshelyet tartalmazó) csoportba. Ha nem két, hanem kettőnél több csoportba osztjuk be őket, akkor a mondott általánosításhoz jutunk. Igennel kell felelni a feladat kérdésére akkor is, ha benne nem-negatív egész számok helyett egész számokat mondunk. Ennek megvilágítása érdekében a végtelen $\begin{array}{c}{\displaystyle \left(1+x\right)\left(1+x^2\right)\left(1+x^4\right)\left(1+x^8\right)\text{...}}\end{array}$ szorzatot tekintjük. Ha itt a beszorzást formálisan elvégezzük, $x$ minden nemnegatív egész kitevőjű hatványának összege adódik eredményül. Ha a szorzat tényezőit két csoportba szedve, pl. csak a páratlanadikokat, majd csak a párosadikokat szorozzuk össze, akkor az adódó két kifejezésben fellépő kitevők példát adnak olyan $A$, $B$ halmazokra, amilyenekről a feladat szólt. Ha most a fenti szorzat helyett az $\begin{array}{c}{\displaystyle \left(1+x\right)\left(1+x^{-2}\right)\left(1+x^4\right)\left(1+x^{-8}\right)\text{...}}\end{array}$ szorzatot tekintjük, akkor a beszorzás $x$ minden egész kitevőjű hatványának összegét adja, s a tényezők két csoportba szedésekor fellépő kitevőhalmazok az egész számok körében kimondott általánosítás helyességét támasztják alá.    Hajós György