Cím: Az 1966. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása. Haladók versenye, a speciális matematikai osztályok versenyének feladatai
Szerző(k):  Lőrincz Pál ,  Tusnády Gábor 
Füzet: 1967/április, 146 - 149. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Hozzuk egyszerűbb alakra a következő összeget:

S=1⋅2⋅...⋅k+2⋅3⋅...(k+1)+3⋅4⋅...⋅(k+2)+...+n⋅(n+1)⋅...⋅(n+k-1).



(Az összeg n tagból áll, minden tagja k számú tényező szorzata.)
 
Megoldás. Tüntessük fel az összeg jele mellett indexben tagjainak számát, így a fenti kifejezés Sn⋅n=2 és 3 esetén az összeg így alakítható:

S2=1⋅2⋅...⋅k+2⋅3⋅...⋅k⋅(k+1)=2⋅3⋅...⋅k(1+k+1)==2⋅3⋅...⋅k⋅(k+1)⋅(k+2)k+1,S3=S2+3⋅4⋅...⋅k⋅(k+1)⋅(k+2)==3⋅4⋅...⋅(k+2)⋅(2k+1+1)=3⋅4⋅...⋅(k+2)⋅(k+3)k+1.



Az utolsó alak számlálója mindkét esetben k+1 egymás utáni természetes szám szorzata, első tényezőnek véve az összeg tagjainak számát, a nevező pedig k+1. Ebből azt sejtjük, hogy
Sn=n⋅(n+1)⋅...⋅(n+k)k+1.(1)

(Könnyű látni, hogy ez n=1 esetén is érvényes.) Ezt fogjuk bizonyítani a teljes indukció módszerével.
Tegyük fel, hogy (1) helyes n-nek valamilyen i értékére. Ekkor öröklődik n=i+1-re is, mert

Si+1=Si+(i+1)⋅(i+2)⋅...⋅(i+k)==i⋅(i+1)⋅...⋅(i+k)k+1+(i+1)⋅(i+2)⋅...⋅(i+k)==(i+1)⋅(i+2)⋅...⋅(i+k)⋅(ik+1+1)==(i+1)⋅(i+2)⋅...⋅(i+k)(i+k+1)k+1,



tehát (1) helyes minden pozitív egész n-re. Másrészt (1) ‐ mint egytagú kifejezés ‐ egyszerűbbnek tekinthető az eredeti, adott alaknál. Ezzel a feladatot megoldottuk.
 
Megjegyzés. A speciális osztályok matematikai gyakorlatainak anyagában szerepelnek a kombinatorika elemi fogalmai és feladatai. Ezek felhasználásával eredményünket az alábbiak szerint értelmezhetjük.*
A talált

1⋅2⋅...⋅k+2⋅3⋅...⋅k⋅(k+1)+...+n⋅(n+1)⋅...⋅(n+k-1)==n⋅(n+1)⋅...⋅(n+k)k+1


egyenlőséget k!-sal osztva a bal oldal tagjaiban felismerjük azoknak a k-ad osztályú kombinációknak a számát, amelyeket rendre k, k+1, ..., n+k-1 (különböző) elemből lehet képezni, a jobb oldalon pedig n+k elem k+1-ed osztályú kombinációinak számát. Azt kaptuk tehát, hogy
Ck(k)+Ck+1(k)+...+Cn+k+1(k)=Cn+kk+1,
illetőleg a másik szokásos jelöléssel
(kk)+(k+1k)+...+(n+k+1k)=(n+kk+1).

Gondoljunk konkrétan az 1, 2, ..., n+k számokból képezhető k+1-ed osztályú kombinációkra. Igy a bal oldal a kombinációk számát legkisebb számuk szerint csoportokba foglalva adja meg. Az egymás utáni tagok azoknak a kombinációknak a számát adják, amelyeknek legkisebb száma rendre
n,n-1,...,1
ekkor ugyanis a további k számot a nagyobbakból választjuk minden lehetőség szerint, azok száma pedig rendre
k,k+1,...,n+k-1.
n+1-et már nem választhatjuk a k+1-ed osztályú kombináció legkisebb számának.
Hasonlóan mondhatjuk, hogy a bal oldal egymás utáni tagjai azoknak a kombinációknak a számát jelentik, amelyek legnagyobb száma rendre
k+1,k+2,...,k+n.

 
2. feladat. Milyen összefüggés áll fenn A és p között, ha
A=x2-3y23x2+y2,(2)
továbbá
pxyx2-(2+p)xy+2py2-yx-2y=12?(3)

 
Megoldás. Az x=y=0 esetet nyilvánvalóan ki kell zárnunk, de nem lehet y=0, x≠0 sem, mert akkor (3) nem teljesül, ha pedig x=0, y≠0, akkor A=-3, (2) pedig az 12=12 azonosságba megy át, és így p akármi lehet, nem áll tehát fenn összefüggés A és p közt. Tegyük fel a továbbiakban, hogy sem x, sem y nem 0. Feltesszük továbbá, hogy a (3)-beli nevezők egyike sem 0. Az első nevező szorzattá alakítható: (x-2y)(x-py), tehát x≠2y, x≠py. A törteket y2-nel, illetőleg y-nal egyszerűsítve (2) jobb oldala és (3) bal oldala az x/y=t változó kifejezéseként írható:
A=t3-33t2+1,(2')pt(t-2)(t-p)-1t-2=12.(3')

(3')-t szorozva 2(t-2)(t-p)-vel, rendezés után
t2-3pt=t(t-3p)=0.

Eszerint, mivel t≠0, a (3) feltevés azt fejezi ki, hogy t értéke csak 3p lehet. Így a keresett összefüggés (2')-ből
A=9p2-327p2+1.

 
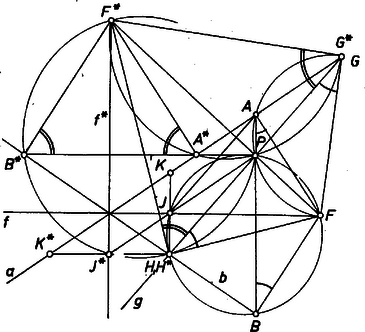
3. feladat. Adott a síkban két metsző egyenes, a és b, és egy pont, P. A két egyenes egyik szögfelezőjét jelöljük f-fel. (P nincs rajta sem a-n, sem b-n, sem az egyenesek szögfelezőin.) Messe a P-n átmenő, t-re merőleges egyenes a-t az A pontban. Állítsunk A-ban az a-ra merőleges egyenest, messe ez f-et az F pontban. Végül állítsunk merőlegest P-ben az FP egyenesre. ‐ Bizonyítsuk be, hogy P felezi az FP-re merőleges egyenesnek az a és b közé eső szakaszát.
 
I. megoldás. Messe a kérdéses merőleges a-t G-ben, b-t H-ban, ekkor elég belátnunk az FGH és FHG szögek egyenlőségét, hiszen így FGH egyenlő szárú háromszög, és FP magassága felezi a GH alapot. Válasszuk a betűzést úgy, hogy a és b közül a P-hez közelebbi legyen a.
Legyen először f az a és b közti négy szögtartomány közül annak a felezője, amelyikben P benne van, és messe az f-re merőleges PA egyenes b-t B-ben. P az AB szakaszon van, F ugyanebben a szögtartományban adódik, és G az FP egyenesnek azon a partján, amelyiken A van, B és H pedig a másik partján. FPAG és FPHB húrnégyszögek, mert az FG szakasz A-ból és P-ből, FH pedig P-ből és B-ből derékszögben látszik, hiszen B az A tükörképe f-re, és így FB merőleges b-re. Mivel még P a GH szakasz belső pontja, azért
FGH∢=FGP∢=FAP∢=FBP∢=FHP∢=FHG∢.
Ezt akartuk bizonyítani, ebből ‐ mint láttuk ‐ az állítás egyszerűen következik.
 
 

f-ként a P-t tartalmazó a, b szögtartománnyal szomszédos szögtartományok felezőjét véve ‐ legyen ez f*, és az így szerkesztett pontok A*, F*, G*, H* és B*, meggondolásunk csak abban változik, hogy F*P szétválasztja az A*, G* pontpárt és hogy A* van a PB* szakaszon. A megfelelő húrnégyszögekből ekkor is

F*G*H*∢=F*G*P∢=180∘-F*A*P∢=F*A*B*∢=F*B*A*==F*B*P∢=F*H*P∢=F*H*G*∢.


Ezzel a bizonyítást befejeztük.
 
II. megoldás. Az állítás fordítottját bizonyítjuk, megmutatjuk, hogy ha P felezi a g egyenesnek az a és b közé eső GH szakaszát, akkor FP merőleges g-re. Ebből az állítás akkor következik, ha azt is belátjuk, hogy P a rajta átmenő egyenesek közül csak egynek felezi az a és b közti szakaszát. Ez abból adódik, hogy pl. G-t b-nek P-re vett tükörképe metszi ki a-ból.
Messe a H-n átmenő, f-re merőleges egyenes f-et J-ben, a-t K-ban. H és K tükrös pár f-re, ezért J felezi HK-t, és mivel még HK∥AP, azért PAJ a KHG háromszög középháromszöge, PJ∥a és AJ∥g. Így F a PAJ háromszög magasságpontja, hiszen itt metszi egymást a J-ből és A-ból kiinduló magasságvonal. Ezért PF merőleges AJ-re és a vele párhuzamos g-re is, amint állítottuk.
Ezzel a bizonyítást befejeztük. Bizonyításunk mindkét szögfelezőre egyformán érvényes.
 
 Lőrincz Pál ‐ Tusnády Gábor
*Az általános tantervű osztályok tanulói részére ajánljuk: Kürschák J.‐Hajós Gy.‐Neukomm Gy.‐Surányi J.: Matematikai versenytételek I., 3. kiadás, Tankönyvkiadó, Budapest, 1965, 26. o.