|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Bizonyítsuk be, hogy bármely társaságban található két olyan ember, akiknek abban a társaságban ugyanannyi ismerősük van.
I. megoldás. Legyen a társaság tagjainak száma ; mivel társaságról van szó, . Ekkor a társaság egy tagjának , vagy , vagy , vagy ismerőse lehet jelen. Nem lehet azonban olyan is, akinek nincs ismerőse a társaságban, meg olyan is, akinek ismerőse van, hiszen az utóbbinak a társaság minden tagja ismerőse, és ez legalább ismerőst jelent, mert . Így, ha mindenki megmondja, hány ismerőse van jelen, akkor ember legfeljebb különböző számot mondhat, tehát legalább ketten ugyanazt a számot mondják, vagyis ugyanannyi ismerősük van jelen.
II. megoldás. Legyen a társaság -tagú; , mert embert nem mondunk társaságnak. Ekkor egy embernek , vagy , vagy , vagy ismerőse lehet jelen, ez összesen lehetőség, tehát mindegyiknek elő kellene fordulnia, ha mindenkinek más-más számú ismerőse volna jelen. De ekkor a senkit sem ismerő távozásával senki ismerőseinek a száma nem változnék, tehát a visszamaradó (legalább ) ember közül is mindenkinek más-más számú ismerőse volna jelen. Ekkor azonban ezek közt is volna, akinek nincs jelen ismerőse. Mivel ennek az eltávozott sem ismerőse, tehát az eredeti társaságban legalább embernek nem lett volna ismerőse, holott éppen azt tettük fel, hogy eredetileg mindenkinek más számú ismerőse volt jelen. Ez a feltevés tehát helytelen-nek bizonyult, s így a feladat állítása a helyes.
2. feladat. Bizonyítsuk be, hogy ha egy húrnégyszög átlóinak metszéspontján átmenő egyenesnek a négyszög belsejébe eső szakaszát felezi, akkor felezi a körülírt körnek az említett egyenesre eső húrját is.
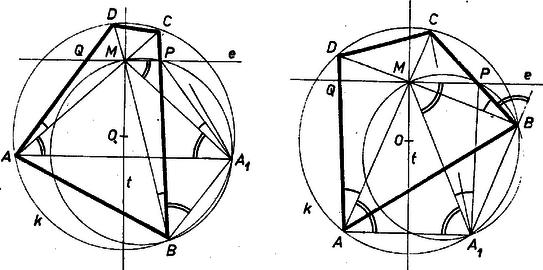
I. megoldás. Legyen az egyenesnek a négyszög belsejébe eső szakasza , és felezze -t. Ha azonos a négyszög egyik átlójával, akkor a feladat állítása semmitmondó. Feltehetjük tehát, hogy a két átló között halad, így a négyszöget szemközti oldalaiban metszi. Válasszuk úgy a betűzést, hogy a négyszög , a oldalszakaszán legyen. Tükrözzük az csúcsot a szakasz felező merőlegesére, kapjuk az pontot. Megmutatjuk, hogy rajta van az négyszög köré írt körön.
, hiszen mindkettő merőleges -re. , mert váltószögek, a tükrözés miatt, és ez utóbbi azonos a szöggel, tehát . (Az 1.a - 1.b ábrákon t szétválasztja -t és -t.) Az , , , pontok egy körön vannak, hiszen | |
egyrészt a kerületi szögek tétele, másrészt a tükrözés miatt, és mert az , pontok az egyenesnek ugyanazon az oldalán vannak. Ha az és pontok az egyenes azonos oldalán vannak, akkor a és pontok is ugyanazon az oldalán vannak az egyenesnek, így az szakasz a és pontokból egyenlő szögben látszik.
 1.a és 1.b ábra
Mivel és szögek azonosak, a és szögek pedig egyenlőek, az szakasz is ugyanakkora szögben látszik az és pontokból, tehát valóban rajta van az , , pontok által meghatározott körön.
Ugyanezt kapjuk, ha az egyenes elválasztja az és pontokat (1.b ábra). Ebben az esetben az egyenes is elválasztja az és pontokat, az és szögek tehát -ra egészítik ki egymást, így az és szögek is -ra egészítik ki egymást, és most emiatt lesz a körön.
Hasonlóan adódik állításunk, ha és a -nek ugyanazon oldalán van (2. ábra).
Mivel a körön van, az szakasz felezőmerőlegese, a egyenes a kör átmérője, így felezi a rá merőleges egyenesre eső húrt, amint azt bizonyítanunk kellett.
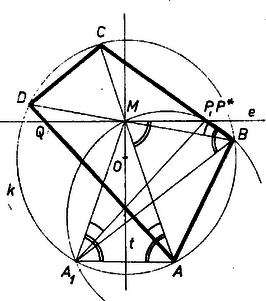 2. ábra Megjegyzések. 1. Lényegében ugyanígy halad a megoldás, ha a egyenest eleve az -en átmenő átmérőnek vesszük fel (2. ábra). Ebben az esetben nyilván a körre kerül, ellenben bizonyítanunk kell, hogy is merőleges -re. Mivel ezt nehéz közvetlenül belátni, a versenyzők többsége a feladat állításának a fordítottját bizonyította, hogy ti. ha egy az -en átmenő egyenesnek a körre eső húrját felezi, akkor felezi a négyszögbe eső szakaszát is. Ha és kör középpontja azonos, akkor - mint az könnyen látható - minden egyenesnek megvan mindkét tulajdonsága. Ha és nem azonos, akkor nyilván akkor felezi az egyenesre eső húrt, ha . Ha tehát belátjuk egyrészt, hogy ebből következik, hogy felezi az egyenes négyszögbe eső szakaszát, másrészt, hogy olyan egyenes is csak egy van, amelyiknek a négyszögbe eső szakaszát felezi, akkor e kettő együtt kiadja a feladat állításának a bizonyítását. Az első rész a fenti megoldáshoz hasonló módon bizonyítható: mivel , az , , , pontok egy körön vannak, tehát , viszont ez teljesül a pont tükrözéséből származó pontra is: , tehát azonos -vel. A második rész bizonyításával kapcsolatban a II. megoldás első mondataira utalunk.
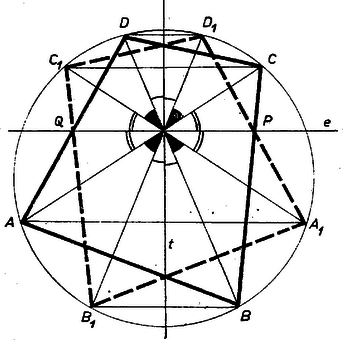
2. Ha az egész négyszöget tükrözzük az egyenesre, akkor és a megfelelő oldalak metszéspontja lesz, és azt kell megmutatnunk, hogy . Valóban, az pontban keletkezett szög közül a 3. ábrán azonosan jelzettekről könnyen kimutatható, hogy egyenlőek, amiből már következik az állításunk. Ebben az esetben azonban fel kell használnunk, hogy olyan egyenes, amelyen levő húrt felezi, ill. olyan egyenes, amelynek a négyszögre eső szakaszát felezi, csak egy van, mert csak ennek belátása után következik a feladatunk állítása abból, hogy az általunk adott konstrukció mellett a egyenesnek mindkét tulajdonsága megvan.
 3. ábra
3. Azt viszont, hogy ha felezi -t, akkor a szakasz felező merőlegese átmegy a kör középpontján, tükrözés nélkül is beláthatjuk (4. ábra). Legyen az , a szakasz felezőpontja. Feltehetjük, hogy a pontból a szakasz látszik hegyesszög alatt, ekkor az , háromszögek hasonlósága miatt a pontból ugyanakkora szög alatt látszik a oldal. Attól függően, hogy a , ill. a pont a , ill. szakaszra esik-e vagy sem, az , ill. szakasz vagy , vagy szög alatt látszik a , ill. pontokból.
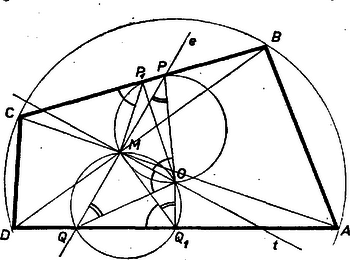 4. ábra
Keressük meg a egyenesnek az egyenes és csúcsokat tartalmazó oldalára eső félegyenesén azt az pontot, ahonnan az és szakaszok szög alatt látszanak. Akkor az , , , , ill. , , , pontok egy-egy körön lesznek, melyeknek és átmérői, az , szögek tehát derékszögek, így a kör középpontjával azonos.
II. megoldás. Tükrözzük az négyszöget és a köré írható kört a négyszög átlóinak metszéspontjára. Ha mindkét átlót felezi, a négyszög és a kör önmagába megy át, ebben az esetben az ponton átmenő egyeneseknek a négyszögbe és a körbe eső szakaszát is felezi , állításunk tehát igaz. Ha csak egy átlót felez, válasszuk úgy a betűzést, hogy ez az átló legyen, és teljesüljön, hogy . Akkor a tükrözés során az és csúcsok helyet cserélnek, a csúcs és a belőle kiinduló , oldalak a négyszög belsejébe, a csúcs és a belőle kiinduló , oldalak a négyszögön kívülre kerülnek, így csak az átlónak felezi a négyszögbe eső darabját, viszont egyben a -nak is húrja, állításunk tehát ismét nyilvánvaló.
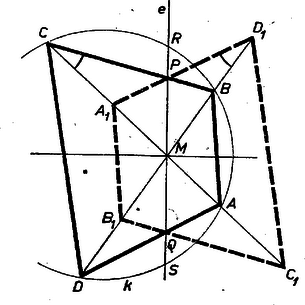 5. ábra
A továbbiakban feltehetjük tehát, hogy egyik átlót sem felezi. Válasszuk úgy a betűzést, hogy az átlón , a átlón legyen az -hez közelebbi csúcs (5. ábra). A tükrözés során kapott és csúcs az eredeti négyszög belsejében lesz, a , csúcs pedig azon kívülre kerül, így csak a és , ill. és szakaszok metszhetik egymást a tükrözött és az eredeti négyszög kerületén. Legyenek a metszéspontok és , ekkor csak a egyenesnek felezheti a négyszögbe eső szakaszát. A kapott és háromszögek hasonlóak, hiszen -nél levő szögük egyenlő és | |
emiatt A tükrözés miatt viszont és , tehát azaz a és pontoknak a körre vonatkoztatott hatványuk egyenlő. (Ismeretes, hogy egy körhöz adott pontból húzott szelő darabjainak szorzata független a szelő választásától - ezt a szorzatot nevezzük a pont körre vonatkozó hatványának.) Ebből már következik a bizonyítandó állítás, hiszen ha a egyenes a kört az , pontokban metszi, és , akkor és mindkét oldalból -t levonva kapjuk, hogy ahol , tehát valóban , azaz .
Megjegyzések. 1. Azt, hogy a , pontok -ra vonatkozó hatványa egyenlő, tükrözés nélkül is beláthatjuk.
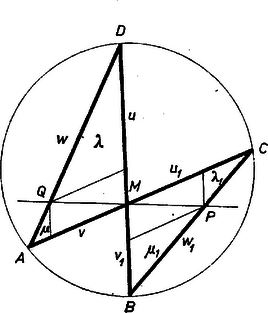 6. ábra
Húzzunk -n és -n át párhuzamosakat az , átlókkal (6. ábra), így az egymáshoz hasonló , háromszögek mindegyikét egy paralelogrammára és két háromszögre vágtuk fel. A keletkezett négy kis háromszög hasonló az eredeti háromszögekhez, a paralelogrammák is hasonlók, és mivel és átlóik egyenlők, egybevágóak is. Legyenek az és háromszögek oldalai rendre , , , ill. , , , és a , , ill. , alapú kis háromszögek oldalai a megfelelő nagy háromszögek oldalainak rendre , , ill. , -szeresei. Az átlóval párhuzamos oldalt a és alapú, a átlóval párhuzamos oldalt pedig a , alapú háromszögben felírva kapjuk, hogy ezeket összeszorozva
Az , háromszögek hasonlósága miatt ezt a két aránypárt összeszorozva kapjuk, hogy Ebből következik, hogy ami épp a bizonyítandó egyenlőség:
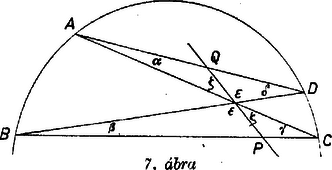
Beláthatjuk ezt a szinusztétel felhasználásával is (7. ábra):
| |
2. Ha felhasználjuk, hogy két egymást metsző körre azon pontok mértani helye, amelyeknek a két körre vonatkozó hatványa egyenlő, a két kör metszéspontjain átmenő egyenes, akkor megoldásunk rövidebben is befejezhető. A pontnak a körre vonatkozó hatványa , a körre vonatkozó hatványa , mivel ez a két szorzat az húrnégyszögben egyenlő, - és hasonló módon is - rajta van a és körök hatványvonalán, így a két kör centrálisa merőleges -ra, a tükrözés miatt átmegy -en, és felezi a kör egyenesre eső húrját.
3. feladat. a) Keressünk meg minden olyan természetes számot, amelynek négyzetében mindegyik számjegy helyébe ugyanazzal a pozitív számmal kisebb jegyet írva, a keresettnél -vel kisebb természetes szám négyzetét kapjuk.
b) Hány megoldása van a feladatnak tetszés szerinti alapú számrendszerben?
Megoldás. a) Legyen a keresett szám , a nála -vel kisebb szám , és számjegyeinek száma . Jelöljük a darab -essel felírt számot -vel, ekkor a feladat szerint
A bal oldalon , tehát , amit -vel osztva
Így miatt , azaz . Viszont és jegyeinek száma , ezért , , és , tehát
A két szélső tagból kapott egyenlőtlenség alapján , amiből következik, hogy . Nem lehet azonban , mert , tehát , , és kétjegyű szám, tehát egyjegyű. Mivel így , azért , és (2)-re is tekintettel , és szóba jövő értékei:
Ezekkel
A harmadik és negyedik értékrendszer esetében második számjegye kisebb -nél, ezek nem megoldásai a feladatnak. Az első két értékrendszer a feladat minden követelményét kielégíti, a keresett számok tehát és .
b) Legyen a számrendszer alapszáma . Az előző meggondolások egy részét átvehetjük, a többjegyű számokat az -alapú számrendszerben értve. (1), (2) és (3) továbbra is érvényes, és a egyenlőtlenség is érvényes marad, tehát és , hiszen is változatlanul fennáll.
Nem lehet sem , sem . Ugyanis a számjegy -nél kisebb, mert különben -ből az ugyanannyi jegyből álló számot levonva nem kaphatunk pozitív maradékot. Ilyen pozitív nincs, ha ; az esetben pedig csak lehetne. Ekkor a (3)-ból és (2)-ből adódó összefüggés szerint páratlan, így értéke nem lehet , tehát (4)-et figyelembe véve , így , és a -alapú számrendszerben már több mint -jegyű.
Minden alapszám esetében (4) alapján , tehát , és kétjegyű, ezért , egyjegyű, azaz . és alapján szóba jövő értékei , , , , , ahol az a legnagyobb egész szám, amelyre még , azaz .
Ha páros, , akkor , ha páratlan, , akkor , tehát mindenképpen az a legnagyobb egész szám, amelyik még nem nagyobb -nél, a szokásos jelöléssel .
Minden ilyen esetén és kielégíti (1)-et és (2)-t, továbbá kétjegyű, hiszen miatt
Az , , számhármasok akkor megoldásai feladatunknak, ha mindkét számjegye külön-külön -vel nagyobb megfelelő jegyénél. Ha ez a feltétel a második jegyekre teljesül, vagyis az összeadást jegyenként végezve (először a , majd az tagot adva hozzá) első számjegye ugyanaz, mint első jegye, akkor teljesül az első jegyekre is. Így ugyanis nem viszünk át maradékot, az tag az -nek helyi értékű jegyét növeli -vel, és első jegyét adja, mert itt nem lehet maradékátvitel, hiszen .
A második jegyek nagyságviszonyának vizsgálatát megkönnyíti a következő észrevétel: Legyen , ekkor és második számjegye megegyezik, hiszen így , tehát , különbségük osztható -val. Elegendő tehát azoknak az -értékeknek a számát meghatározni, melyek négyzetének második jegye kisebb a náluk -gyel kisebb szám négyzetének második jegyénél. Ez miatt csak úgy lehetséges, hogy első jegye kisebb első jegyénél, mégpedig pontosan -gyel, hiszen .
Eszerint az számok négyzetében első jegyként minden számjegy előfordul első jegyéig ( esetén is), és minden előforduló kezdő számjegyhez pontosan megfelelő -érték tartozik, mégpedig a legkisebb azok közül a számok közül, amelyeknek négyzete az illető számjeggyel kezdődik. Ha első számjegye , akkor -hoz nem tartozik megoldása a feladatnak, hiszen ekkor a szám négyzetének második számjegye mindig kisebb második jegyénél. Így a feladatnak megfelelő -értékek (és , , értékrendszerek) száma egyenlő első számjegyével. Ezt megadja az hányados egész része, tehát a megoldások száma
Eredményünk megfelel az a) részben kapott eredményünknek, hiszen esetén , és első jegye .
Tusnády Gábor
|
PDF | MathML 