Cím: Az 1966. évi Arany Dániel tanulóversenyek I. fordulóján kitűzött feladatok megoldása (kezdők versenye)
Szerző(k):  Scharnitzky Viktor 
Füzet: 1967/január, 1 - 4. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Két egybevágó paralelogramma egyenlő oldalai párhuzamosak. Mindkét paralelogrammában megjelöljük a csúcsokat, az oldalak felezőpontjait, és az átlók metszéspontját. Minden lehetséges módon kiválasztunk egy pontot az első paralelogramma megjelölt pontjai közül, valamint egy pontot a második paralelogramma megjelölt pontjai közül, és megszerkesztjük a két kiválasztott pont közti szakasz felezőpontját.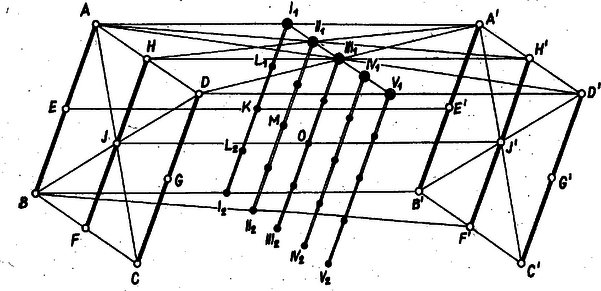
Hány különböző felezőpontot kapunk így?

 
Megoldás. Jelölje az egyik (P) paralelogramma csúcsait A, B, C, D, az AB, BC, CD, DA oldalak felezőpontját rendre E, F, G, H, az átlók metszéspontját J. A másik (P') paralelogramma ebből eltolással kapható meg; legyenek a megfelelő megjelölt pontjai A', B', C', D', E', F', G', H', J' (1. ábra).
 
 
1. ábra
 

Mind a két paralelogramma megjelölt pontjaiból egymástól függetlenül 9-féleképpen választhatunk ki 1-1 pontot, ezek 9⋅9=81 szakaszt határoznak meg. A különböző felezőpontok számának megállapításában P és P' megjelölt pontjaiból egyszerre mindig olyan 3-at-3-at veszünk figyelembe, melyek egy az AB oldallal párhuzamos oldal vagy középvonal pontjai.
Az A, E, B és A', E', B' pontok 9 szakaszt határoznak meg, ezek közül az ABB'A' paralelogramma K középpontja felezi a két átlót és az EE' középvonalat, tehát 3 szakaszt; az AEE'A' és EBB'E' paralelogrammák középpontja L1, illetőleg L2 e paralelogrammák átlóit, tehát 2-2 tekintetbe veendő szakaszt feleznek; az AA' és BB' oldalak felezőpontjai, I1, illetőleg I2 csak ezt az 1-1 szakaszt. A felsorolt pontok az ABB'A' paralelogramma I1I2 középvonalának különböző pontjai, és azt 4 egyenlő szakaszra osztják.
Hasonlóan 5 különböző pontot kapunk az A, E, B és H', J', F' pontok közül egyet-egyet összekötő 9 szakasz felezőpontjaiból, az ABF'H' paralelogramma II1II2 középvonalán. Ez az AH' szakasz felezőpontján megy át és párhuzamos AB-vel, így különbözik az előbbi 5 pontot tartalmazó egyenestől.
Ugyanez az öt pont adódik a H, J, F és az A', E', B' pontok közül egyet-egyet összekötő szakaszok felezőpontjaiból, hiszen pl. az AA'H'H paralelogrammában az AH' és HA' átlók felezőpontja egybeesik, hasonlóan a többi megfelelő szakaszpárok felezőpontjai is. Így ez az 5 pont rendre 2, 4, 6, 4, 2 megrajzolandó szakaszt felez.
5‐5 különböző pont adódik az alább felsorolt két-két ponthármas felezőpontjaiként is, egy-egy az AB-vel párhuzamos egyenesen:

III.A,E,BésD',G',C',IV.H,J,FésD',G',C',V.D,G,C,ésD',G',C';H,J,FésH',J',F',D,G,CésH',J',F';D,G,CésA',E',B';
és az egy oszlopban álló ponthármas-párok ugyanazt az 5 pontot adják, mert pl. az ADD'A' paralelogramma AD' és DA' átlóinak, valamint HH' középvonalának felezőpontja közös, a III1 pont. A III1 és III2 pontokkal meghatározott szakaszon levő 5 pont rendre 3, 6, 9, 6, 3 figyelembe veendő szakaszt felez, a IV1-gyel és IV2-vel meghatározott szakasz pontjai 2, 4, 6, 4, 2 szakaszt, végül az V1V2 szakasz 5 pontja 1, 2, 3, 2, 1 pontot. A sorra vett 9 ponthármas-párban mind a 81 szakasz felezőpontját figyelembe vettük.
A III1- ből kiinduló pont-ötös különböző az I1-ből és II1- ből kiindulótól, hiszen a kezdőpontok az AA', AH', AD' szakaszok felezőpontjai, és összekötő egyenesük AD-vel párhuzamos. Ugyanígy IV1 és V1 is különbözik a többi kiindulópontoktól. Mindezek szerint 5⋅5=25 különböző felezőpontot kaptunk.
 

Megjegyzések. 1. Elindulhatunk a különböző felezőpontok megszámlálásában úgy is, hogy egy kiszemelt pontpár felezőpontjára tükrözzük P'-t‐ ami által a P'-ből kiszemelt pont képe mindenesetre a P-ből kiszemelt pontba esik ‐, és számba vesszük, hogy P' további megjelölt pontjainak tükörképei közül hány esik egybe P-nek egy további megjelölt pontjával. Így a JJ' szakasz O felezőpontjára való tükrözéssel P' mindegyik megjelölt pontjának képe P-nek egy megjelölt pontjába esik, az O pont 9 szakaszt felez, vagyis ugyanerre a fedésre vezet az A és C', az E és G', ... , a H és F' pontpárból való kiindulás. A JE', JF', JG' és JH' szakaszok felezőpontjai 6-6 szakaszt feleznek, mert pl. a JE'-nek M felezőpontjára való tükrözés A'B'-t FH-ra, H'F'-t BA-ra viszi, s így tovább. ‐ Ezen az úton kissé nehézkes a már számba vett pontpárok nyilvántartása.
Egy további elindulási lehetőség: tekintsük az A-ból P' összes megjelölt pontjaiba vezető szakaszok felezőpontjait, ezek P' felére kicsinyített képét adják, vagyis 9 különböző pontot. P'-nek egymás után E-ből, B-ből, F-ből és C-ből való hasonló kicsinyítésekor egybeesések miatt csupán 3-3 új felezőpont adódik, a G-ből és D-ből való kicsinyítéskor már csak 2-2, végül a H-ból és J-ből való kicsinyítéskor már egy sem. Ennek lépésről lépésre való pontos átgondolása szintén hosszadalmasabb a fentinél.
 
2. Könnyű belátni, hogy megállapításaink akkor is érvényesek, ha a két eredeti paralelogramma két különböző síkban van.
 
2. feladat. Hozzuk egyszerűbb alakra a következő kifejezést:
1+a11-a1+a2(1-a1)(1-a2)+a3(1-a1)(1-a2)(1-a3)++a4-a1(1-a1)(1-a2)(1-a3)(1-a4).



 
Megoldás. Adjuk össze először a kifejezés első két tagját, majd adjuk hozzá összegükhöz a harmadik tagot, a kapott összeghez a negyedik tagot, és végül az ötödiket. Így rendre a következő kifejezéseket kapjuk:
1+a11-a1=11-a1,11-a1+a2(1-a1)(1-a2)=1(1-a1)(1-a2),1(1-a1)(1-a2)+a3(1-a1)(1-a2)(1-a3)=1(1-a1)(1-a2)(1-a3),1(1-a1)(1-a2)(1-a3)+a4-a1(1-a1)(1-a2)(1-a3)(1-a4)==1-a1(1-a1)(1-a2)(1-a3)(1-a4).


Az utolsó összeg a számlálóval egyszerűsíthető:
1(1-a2)(1-a3)(1-a4).
(1-a1≠0, különben az eredeti kifejezésnek nem volna értelme.)
 
3. feladat. Határozzuk meg azokat a kétjegyű számokat, amelyeket jegyeik összegével elosztva hányadosul 7-et, maradékul 6-ot kapunk.
 
Megoldás. Legyen a keresett kétjegyű számok egyike xy¯=10x+y. Ekkor a feladat feltétele szerint
10x+y=7⋅(x+y)+6,
és itt
6<x+y,(1)
továbbá x és y olyan egész számok, amelyekre
1≦x≦9,0≦y≦9.(2)
Az egyenlet átrendezése után
x=2y+2.(3)
Ezt a kifejezést (1)-be helyettesítve egyrészt
3y+2>6,azazy>43,
másrészt (2) és (3) alapján
2y+2≦9,azazy≦72.
Mivel y egész, ezért mind a két korlátnak csak a 2 és 3 érték tesz eleget, y=2-höz x=6, y=3-hoz x=8 tartozik, és így a keresett kétjegyű számok 62 és 83. Ezek ki is elégítik a feladat követelményeit.
 
 
2. ábra
 


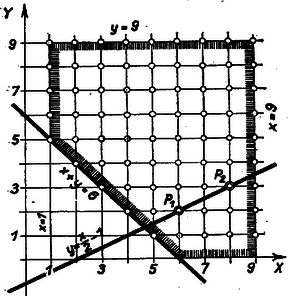Megjegyzések. 1. Az x, y egész számokat egy P pont derékszögű koordinátáinak tekintve, értékeik grafikusan is meghatározhatók. A szóba jöhető P pontok helyét az (1) és (2) egyenlőtlenségek, továbbá az (1) egyenlet szabja meg. A (2) egyenlőtlenségek azt jelentik, hogy a P pontok csak az x=1 egyenestől jobbra, az x=9 egyenestől balra (2. ábra), az y=0 egyenes fölött és az y=9 egyenes alatt, vagy a határoló egyeneseken lehetnek. (1) szerint pedig a P pontok az x+y=6 egyenestől a nagyobb ordináták irányába eshetnek. A P pontok lehetséges helyét vonalkázással jelöltük. Végül (3) azt jelenti, hogy a P pontok csak az
y=x2-1
egyenes egész koordinátájú pontjai lehetnek. Az ábrából leolvasható, hogy minden feltételnek eleget tevő pont csak kettő van, a P1(6,2) és P2(8,3), tehát a keresett számok 62 és 83.
 
2. Számos versenyző tévesen a 20 és 41 számokat is megoldásnak vette, mert 20=2⋅7+6 és 41=5⋅7+6, és nem gondolt arra, hogy az osztás maradéka nem lehet nagyobb az osztónál.
 Scharnitzky Viktor