|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A vektorok mibenléte és a velük végzett legegyszerűbb műveletek (összeadás, kivonás, összetevőkre bontás) ismeretesek a középiskolai tanulmányokból. Vektorokra azonban nemcsak ezek a műveletek értelmezhetők, hanem két vagy több vektor szorzása is. A következőkben bemutatott néhány egyszerű példa azt szeretné illusztrálni, mennyire megkönnyítik az ilyen műveletek a fizikai és geometriai összefüggések, törvények felírását és az azokkal való számolást.
Természetesen egy új műveletet értelmezhetünk teljesen önkényesen, de általában vannak bizonyos célszerűségi szempontok vagy megszorítások. (Például a negatív és tört kitevőjű hatványt úgy definiáljuk, hogy a hatványozás pozitív egész kitevőkre vonatkozó ismert azonosságai továbbra is érvényben maradjanak.) Mivel a vektorokat két adat (nagyság és irány) jellemzi, még a célszerűségi szempontok figyelembevételével is a szorzást többféleképpen értelmezzük.
Vektorok szorzása skaláris mennyiséggel
Legyen tetszőleges valós szám. Az vektoron azt a vektort értjük melynek iránya -éval egyező, illetőleg esetén vele ellentétes, nagysága pedig az -énak -szerese. Ez természetszerűleg adódik a szorzásnak mint ismételt összeadásnak az értelmezéséből.
Könnyen belátható, hogy a szorzás e fajtája asszociatív és disztributív a következő értelemben:
Vektorok skaláris szorzata
és vektorok skaláris szorzatán az skaláris mennyiséget értjük, melynél a két vektor által bezárt (-nál kisebb) szög. Jele: Nyilván érvényes a kommutativitás és disztributivitás: Az asszociatív törvény nem érvényes, hiszen általában . (Itt kétféle szorzás szerepel!) Ennek a szorzásnak az az érdekessége, hogy a szorzat akkor is lehet nulla, ha egyik tényező sem az, hanem egymásra merőlegesek. Két vektor merőleges voltát tehát így fejezhetjük ki: . (A nullvektort bármely vektorra merőlegesnek tekintjük.) Megjegyezhetjük még, hogy . Továbbá, hogy ha (egységvektor), akkor , ami nyilván az vektornak a irányába eső vetülete.
Vektorok vektoriális szorzata
Két vektor vektoriális szorzatán azt a vektort értjük, melynek nagysága ( a két vektor által bezárt, -nál kisebb szög), iránya pedig merőleges a két tényezővektorra, továbbá , és sorrend szerint úgy állnak, mint a jobb kéz egymásra merőlegesen állított hüvelyk-, mutató- és középső ujja. (Jobbsodrású rendszer.)
A meghatározás mutatja, hogy tulajdonképpen irányított területről van szó, mert a vektori szorzat nagysága a két tényező által kifeszített paralelogramma területe (1. ábra).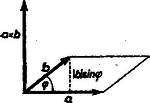
 1. ábra
Itt is igaz, hogy a szorzat lehet nulla, ha a két tényező nem is az; ha ti. a két vektor párhuzamos egymással. Ezért a párhuzamosságot így is kifejezhetjük: . (A nullvektort bármely vektorral párhuzamosnak vesszük.) A felcserélési törvény nem érvényes, mert a sinus-függvény páratlan voltából kifolyólag A csoportosítási törvény sem érvényes, de a disztributivitás igen: Ennek bizonyítása, ha a három vektor egy síkban van, egyszerű, de általános esetben sem nehéz, inkább hosszadalmas, s ezért mellőzzük.
Vegyes szorzat
Természetesen az előbbi szorzatfajtákat különféleképpen lehet kombinálni. Így nyerjük pl. az , ún. vegyes szorzatot, mely könnyen beláthatólag az , és vektorokból alkotott paralelepipedon előjeles köbtartalmával egyenlő, mivel az alapterület és a magasság (2. ábra). Erre érvényes az alábbi azonosság: 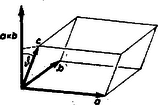így ezt röviden -vel jelöljük.
 2. ábra
Gyakorlásul ellenőrizhetjük a következő összefüggések helyességét: | |
Alkalmazások
Az előbb ismertetett műveletek a geometriában (főként az analitikus geometriában) igen leegyszerűsítik az összefüggések felírását és nagyon szemléletesek. Pl. a cosinus-tétel így írható: .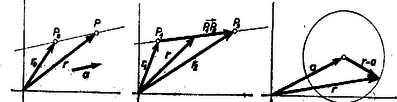
 3., 4. és 5. ábra
Egy ponton átmenő és egy vektorral párhuzamos egyenes egyenlete, ha a helyvektora és a változó vektor: vagy (3. ábra). Két ponton átmenő egyenes egyenlete: | |
A kör egyenlete:
Számunkra azonban fontosabbak a fizikai alkalmazások. A legfontosabbak közül is csak néhányat említünk.
Munka. Ismeretes a erő által elmozdulás alatt végzett munka meghatározása, mely vektori alakban így írható: Valóban ez a szorzat az útnak és az út irányába eső erőkomponensnek a szorzata.
Természetesen görbe vonalú mozgás esetén a megtett utat egyenesnek tekinthető, igen kicsi szakaszokra bontjuk és így képezzük az elemi munkát: , s ezeket összegezzük az egész útra: . Általában ez csak az integrálszámítás segítségével végezhető el. Egyszerűbb esetben azonban nélküle is célhoz lehet jutni. Vegyük például egy matematikai inga esetét, amikor keressük, mennyi munkát végez a nehézségi erő, míg az tömeget vízszintes helyzetből a legmélyebb helyzetbe hozza.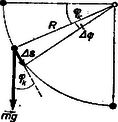
 6. ábra
Osszuk fel a negyedkörívet darab hosszúságú ívre (6. ábra). Legyen egy ilyen ívdarabhoz tartozó központi szög . A -adik osztóponthoz tartozó szögelmozdulás . Így a -adik -hez tartozó elemi munka . A teljes munka: Ezt az összeget kell meghatározni. Mivel nagyon kicsi, azért (relatíve is kis hibát követünk el), , és így
Összegezve | |
A jobb oldal
Ha elég kicsi, akkor tehát , vagyis ha elég nagy, akkor amint várható is volt az energiamegmaradás törvényéből.
A vektoriális szorzás sokszor azáltal is megkönnyíti a törvények felírását, hogy nem kell valamely vektor irányát külön megadni. Vegyük példaként a Biot ‐ Savart-törvényt, melynek ismert alakja (ld. KML 1966. 4. szám)
 7. ábra
Ha figyelembe vesszük a térerősség irányát, láthatjuk (7. ábra), hogy a törvény ilyen alakban egyszerűbben írható
Az ebben az alakban felírt törvény nemcsak a nagyságot, de az irányt is közvetlenül megadja.
Egy másik fontos alkalmazási terület a nyomatékok (momentumok) vektori alakban való értelmezése és használata.
 8. ábra
Általában a tér pontjában adott a vektornak a tér pontjára vonatkozó nyomatékán az vektoriális szorzatot értjük, ahol (8. ábra).
Az vektor különféle fizikai mennyiség lehet. Így beszélünk a sebesség, gyorsulás, erő, impulzus nyomatékáról.
Legyen például a sebesség: , ekkor
-nek az pontra vonatkozó (9. ábra) nyomatéka.  9. ábra
A idő alatt történt elmozdulás vektora közelítőleg , pedig nagyságra a idő alatt súrolt terület kétszeresét adja közelítőleg (háromszög területének kétszerese). Ezért a sebesség momentumának nagysága a területi sebesség kétszerese.
Centrális mozgásoknál, vagyis ahol az erő s ezért a gyorsulás is a mozgás centruma felé mutat, s így az erre merőleges komponens nulla (bolygók mozgása), belátható, hogy a sebesség momentumának nagysága s így a területi sebesség is állandó. Ez pedig Kepler II. törvénye, mely szerint a rádiuszvektor által egyenlő időközökben súrolt területek nagysága egyenlő.
A legfontosabb eset, ha az erővektort jelenti, mert ekkor -ben az erő karja és így tulajdonképpen a forgatónyomatékot adja. Szükség van az irányra is, hiszen a forgatónyomatéknak iránya is van, amit a vektori alak ki is fejez.
A forgatónyomaték vektori alakjával való számolás egyszerűségét mutatja a KML 582. feladatára adható következő megoldás. Legyen az alátámasztási ponttól a félgömb súlypontjához vont vektor. Ekkor a súlyerő forgatónyomatéka . Az esetben a fonál feszítőerejének forgatónyomatéka az alátámasztási pontra (10. ábra)
Mivel és ellentétes irányú, csak akkor lehetséges egyensúly, ha
 10. ábra
 11. ábra
A esetben vektor két pontban hat (11. ábra). Ekkor az összes forgatónyomaték
Az egyensúly feltétele most is , vagyis Ebből következik, hogy azaz a kétfajta feszítőerő egyenlő és egyirányú. Nagysága könnyen kiszámítható, hiszen és .
Így | |
amiből
Érdemes még megemlíteni a szögsebességnek mint vektornak segítségével a forgó mozgás kerületi sebességének értelmezését. Egy tengely körül forgó test kerületi sebessége, felírható vektoriális szorzat alakjában, ha a szögsebességet vektornak tekintjük, éspedig oly módon, hogy annak abszolút értékét a -ban mért nagyság adja, iránya pedig a forgástengely olyan módon, hogy a vektor irányában nézve a forgás az óramutató járásával egyező legyen. Ha a forgásponttól a testhez vont rádiuszvektor, akkor könnyen belátható, hogy (12. ábra).
 12. ábra
Számítsuk ki ennek segítségével egy mozgó merev test kinetikus energiáját. Az tömegű merev test végtelen sok pontból összetettnek fogható fel, melyeknek egymástól való távolsága a mozgás közben állandó. Mozgási energiája az egyes pontok kinetikus energiájának összege. Ha az -edik pont tömege és a sebessége, akkor Ismeretes azonban, hogy egy merev test mozgása mindig felfogható mint az egész testre azonos sebességgel történő transzlációs mozgás és egy pont körül szögsebességgel történő forgás. Ha e ponttól mérjük a rádiuszvektorokat az egyes pontokhoz, akkor tehát s így
Az első tag a test transzlációs mozgási energiája: A második tag így írható: .
azonban a tömegközéppont (súlypont) fogalmából kifolyólag helyettesíthető az mennyiséggel, ahol a tömegközéppont rádiuszvektora a vonatkozási ponttól. Tehát | |
Ha a vonatkoztatási pont a tömegközéppont, mely mindig lehetséges, akkor , s így a középső tag kiesik, vagyis ez esetben .
Ha a test egyik pontja fix, vagyis csak forgómozgás van, akkor ezt választjuk vonatkoztatási pontnak, s így 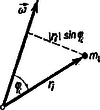miatt az első két tag eltűnik, függetlenül értékétől, és marad | |
 13. ábra
Mivel az forgástengelyre vonatkoztatott tehetetlenségi nyomaték (13. ábra), azért tiszta forgás esetén a mozgási energia Általánosan egy merev test kinetikus energiája tehát amint közismert.
Dózsa Márton
(L. Bodó Zalán cikkét: KML XXII. k. 33. lapon) |
PDF | MathML