Cím: Az 1966. évi fizikai tanulmányi verseny feladatai
Füzet: 1966/október, 81 - 87. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

 

1. Két akkumulátor áll rendelkezésünkre, amelyeknek elektromotoros ereje és belső ellenállása a következő: E1=12,6volt, R1=0,05ohm, E2=12,2volt, R2=0,5ohm. Mi történik, ha a két áramforrást párhuzamosan kapcsoljuk és Rk=2ohm ellenállással zárt áramkört létesítünk?
 
 
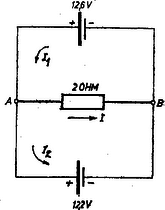1. ábra
 

Megoldás. Különböző elektromotoros erejű áramforrásokat párhuzamosan kapcsolva a nagyobb elektromotoros erejű tölti a kisebbet. AB pontok között egy bizonyos U feszültségkülönbség jön létre (1. ábra). Az első elemből kijövő I1 áram szétoszlik a második elemet töltő I2 áramra és a 2 ohmos ellenálláson átfolyó I áramra:
I1=I2+I.
Az első elem elektromotoros erejének és U kapocsfeszültségének különbsége a belső ellenállásra jutó feszültségesést adja:
12,6V-U=0,05ΩI1.
Hasonlóan a második elemnél:
U-12,2V=0,5ΩI2.
Továbbá felírható Ohm törvénye a külső ellenállásra:
U=2IΩ=2Ω(I1-I2).
Az utolsó három egyenletből álló rendszert megoldjuk, legegyszerűbben úgy, hogy az első kettőből kifejezett I1-et és I2-t az elsőbe helyettesítjük. Az eredmény:
U=1264225V=12,284volt,I1=670225A=6,312amper,I2=38225A=0,169amper.



2. Az ábrán látható rendszer egyenletesen gyorsulva mozog. Adatok: m1=10kg, P1=2kp, m2=2kg, P2=1kp. Mekkora erőt jelez a dinamométer a) ebben az elrendezésben? b) ha a P1 és P2 szerepet cserél, c) ha m1=m2=6kg? Hogyan alakul az eredmény az a) és b) esetben, ha m2 az m1-hez képest elhanyagolható, pl. m2=10gramm? A súrlódástól eltekintünk és a dinamométer tömegét elhanyagoljuk.
 
 
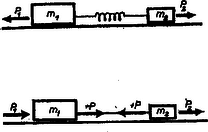2. ábra
 

Megoldás. Foglalkozzunk általánosságban a problémával. A tömegek közös gyorsulása, legyen a, amely akkor pozitív, ha vektornyila jobbfelé mutat. P1 és P2 erők mindegyike akkor legyen pozitív, ha jobbfelé mutat (2. ábra). A fonálban működő P erőt akkor nevezzük pozitívnak, ha a fonál nyújtásra van igénybe véve, vagyis rugalmas ereje befelé húzza össze a tömegeket; negatív P esetében az összekötő fonalat pálcával kell helyettesíteni.
Az egész rendszer együttes tömege m1+m2, a rá ható teljes erő P1+P2, tehát Newton II. törvénye szerint a létrejövő közös gyorsulás:
a=P1+P2m1+m2.
Ez a gyorsulás adódik Newton II. törvényéből akkor is, ha külön-külön írjuk fel az egyes tömegekre:
P1+Pm1=P1+P2m1+m2,P2-Pm2=P1+P2m1+m2.
Ezen egyenletek bármelyikéből kapjuk a fonálerőre:
P=m1P2-m2P1m1+m2.

Táblázatunk különböző adatok esetében tünteti fel a fonálerőt és a keletkező gyorsulást:
 

m1 m2  P1P2Pa  kg kg   kp  kp  kp  102-2+1+7/6-g/12  102+1-2-11/6-g/12  102-1+2+11/6+g/12  66-2+1+1,5-g/12  100-2+1+1-g/10   

 


Közöttük feleletet találunk a feladat kérdéseire. Ha valamelyik tömeg nulla, akkor a fonálerő egyenlő lesz az ezen az oldalon működő külső erővel. A fonálerő eltűnésének feltételét is megtudjuk P képletéből: P1:P2=m1:m2, vagyis mindegyik külső erő a maga tömegét gyorsítja; ekkor az erők csak egyirányúak lehetnek.
Ha egy merev testet több külső erő gyorsít, akkor az egész merev test gyorsulását a külső erők eredőjéből és az egész tömegből könnyen megkapjuk. Közben azonban a merev testben belső erők keletkeznek. Ezekre világít rá ez a feladat.
 

3. Acélgolyóra 20∘C-os petróleumban 21,45, 100∘C-os petróleumban 20 pond felhajtóerő hat. Mekkora e mérés alapján a petróleum köbös hőkiterjedési együtthatója, ha az acél lineáris hőkiterjedési együtthatója 1,2⋅10-51/∘C?
 

Megoldás. Az acél köbös hőkiterjedési együtthatója 3,6⋅10-5. Jelentse az acélgolyó 0 ∘C-on levő térfogatát Va, akkor az acélgolyó térfogata 20∘-on Va(1+3,6⋅10-5⋅20), 100∘-on Va(1+3,6⋅10-5⋅100). Jelentse a petróleum 0∘-os sűrűségét d, köbös hőkiterjedési együtthatóját β, akkor a petróleum sűrűsége 20∘-on d/(1+β⋅20), 100∘-on d/(1+β⋅100). A felhajtóerőt a golyó térfogatának és a folyadék sűrűségének (és g-nek) a szorzata adja meg;
 


20∘-on:
Va(1+3,6⋅10-5⋅20)dg1+β⋅20=21,45,
100∘-on:
Va(1+3,6⋅10-5⋅100)dg1+β⋅100=20.
E kettő osztásával:
(1+3,6⋅10-5⋅20)(1+β⋅100)(1+3,6⋅10-5⋅100)(1+β⋅20)=21,4520.
Minden ismeretlen adat kiesett, ez elsőfokú egyenlet β számára. A megoldás: β=0,963⋅10-31/∘C.
 


A II. forduló feladatai
 

1. r sugarú, m tömegű abroncsot függőleges síkban, a talaj fölött, középpontja körül ω0 szögsebességgel ,,visszafelé'' megforgatva úgy dobunk el, hogy középpontjának sebessége az eldobás irányában v0. Mekkora ω0-val érhető el, hogy az abroncs talajtérés utáni mozgása során visszaforduljon (visszafelé haladjon)? Mekkora ω0 esetén lesz a visszafelé haladó abroncs sebessége v0?
 
 
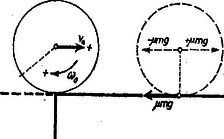3. ábra
 

Megoldás. Kezdetben, a felülethez való hozzáérés előtt az abroncs középpontjának vízszintes sebessége v0, jobbra számítva pozitív előjellel (3. ábra) és az abroncs forgásának szögsebessége ω0, pozitívnak számítva, ha iránya egyezik az óramutató járásával; a kerületi pont sebessége a középponthoz viszonyítva ω0r. v0 és ω0 egymástól függetlenül, tetszés szerint megadható adatok.
Először legyenek olyanok a kezdeti adatok, hogy ω0r<v0. A felülethez való hozzáérés pillanatától kezdve a felület mentén nagyobb a középpont jobbra tartó sebessége, mint a lent érintkező kerületi pont középponthoz viszonyított balra irányuló sebessége, ezért nincs sima legördülés, a kerék köszörül. A kerületi pont mentén fellépő súrlódási erő μmg és balra mutat. Hozzáveszünk a középpontban ±μmg erőket. -μmg erő lassítja a középpont mozgását, a lassító gyorsulás μg. Ennek hatása alatt a középpont egyenletesen lassuló mozgást végez, amelynél vc=v0-μgt. A +μmg erő és az eredeti μmg súrlódási erő μmgr forgatónyomatékot jelent, amely gyorsítja a középpont körüli forgást. A forgás szöggyorsulása β= forg. nyom.: tehetetl. ny. =μmgr/mr2=μg/r. Tehát a szögsebesség mint az idő függvénye: ω=ω0+μgt/r. Ha a kerületi pontnak a középponthoz viszonyított sebességét kérdezzük, ez vk=ωr=ω1r+μgt. Ezek szerint a középpont μg gyorsulással lassabbodva, a kerületi pont μg gyorsulással gyorsabbodva mozog. A forgó mozgás fékezi a haladást, a haladó mozgás gyorsítja a forgó mozgást. Ez a folyamat addig tart, amíg vc és vk egyenlővé nem lesz. Ekkor ér véget a mozgás változása, innentől kezdve sima legördülés áll be, a középpont sebessége valamilyen vr érték, és a szögsebesség ωr=vr/r. Tegyük egyenlővé vc-t és vk-t:
v0-μgt=ω0r+μgt.
Innen a lassítás időtartama t=v0-ω0r2μg.

Ezt az időt akár vc, akár vk képletébe helyettesítve megkapjuk a középpont végső sebességét, amellyel a lassítási folyamat végén továbbgurul:
vr=v0+ω0r2.(1)
Látható, hogy ez a végsebesség a középpont és kerületi pont kezdeti sebességének a számtani középértéke. μ, a súrlódási együttható számértéke e tekintetben lényegtelen.
 
 
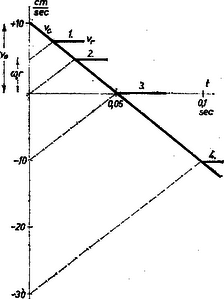4. ábra
 

4. ábránk grafikusan mutatja meg a középpont mozgásának fékeződését és a forgás felgyorsulását, ha v0=10cm/s, r=5cm, μ=0,2, g=1000cm/s2. A középpont vc sebességének grafikonja +10-ből kiinduló, süllyedő egyenes (vastag vonal). Az 1. szaggatott vonal a forgás kerületi sebességének a növekedését mutatja, ha kezdetben ω0=1, ω0r=5cm/s; a végső sebesség közösen 7,5cm/s lesz. Ha forgás nélkül dobjuk oda az abroncsot ω0r=0 (2. vonal), akkor a végsebesség 5cm/s. Ha ellentétes forgásiránnyal, ω0r=-10cm/s-mal dobjuk oda az abroncsot, akkor a végsebesség nulla, az abroncs állva marad (3. vonal); ez a felelet a feladat első kérdésére. Ennél gyorsabb ellentétes kezdeti forgásnál a középértékként keletkező végső sebesség negatív, vagyis az abroncs visszafelé gurul, például ω0r=-30cm/s-nál a végső sebesség -10cm/s (4. vonal); ez a válasz a feladat második kérdésére.
 

(1) képletünkből, a kezdeti v0-ból és ω0-ból kiszámítható a végső sebesség. (1) megoldása ω0-ra:
ω0=2vr-v0r.
A feladat első kérdésében a határesetben vr=0, ezért ω0=-v0/r. Ennél nagyobb abszolút értékű, visszafelé forgó kezdeti szögsebesség szükséges ahhoz, hogy az abroncs megállás után elindulhasson visszafelé. A második kérdésben vr=-v0, tehát ω0=-3v0/r.
Ha a kezdeti feltétel olyan, hogy ω0r>v0, akkor a forgás gyorsítja fel a középpont haladását és a középpont haladási sebessége fékezi a forgást. A végsebességre most is (1) érvényes. Ha ω0r=v0, akkor semmi sem történik, az abroncs mozgásának megváltozása nélkül gurul tovább a felületen.
 

2. α hajlásszögű lejtőn a lejtő síkjával β szöget bezáró erővel, egyenletes mozgással húzunk fel egy testet. A test és a lejtő között a súrlódási együttható μ. Milyen határok között változhat a β szög, hogy a testet fel lehessen húzni a lejtőn?
 
 
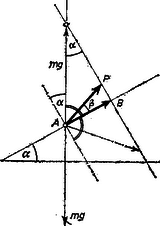5. ábra
 

Megoldás. Először tekintsük a súrlódás nélküli lejtőt (5. ábra). Az A pontban levő testnek a lejtőn egyensúlyban tartásához valamilyen P erő kell, amelynek nagysága abból következik, hogy lejtő menti vetületének mgsinα-nak kell lennie, AB=mgsinα. Ha P erő a lejtőhöz képest β szöget zár be, akkor is AB-nek kell lennie a lejtő menti vetületének. Ebből azonnal következik, hogy az mg súly felhúzásához alkalmas erők végpontjainak mértani helye B-ben a lejtőre húzott merőleges. Ez a mértani hely az A-ban emelt függőlegest X-ben metszi és azonnal látszik, hogy AX=AB/sinα=mg. Ennél balrább nem kerülhet a P erő végpontja, mert akkor leemelné a tárgyat a lejtőről. Eszerint a súrlódás nélküli esetben β szög számára lehetséges a pozitív irányban 0∘-tól 90∘-α-ig, negatív irányban a 0-tól -90∘-ig terjedő szögtartomány.
 
 
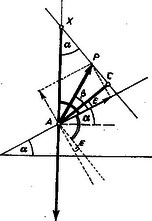6. ábra
 

Most lássuk a súrlódásos esetet (6. ábra). P erő lejtőre merőleges összetevője Psinβ, ezért a tárgyat mgcosα-Psinβ erő nyomja a lejtőhöz és így a súrlódási erő μ(mgcosα-Psinβ. P erő Pcosβ lejtő menti összetevőjének az mgsinα súlyösszetevőt és a súrlódási erőt kell egyensúlyoznia, ha a terhet egyenletesen fel akarjuk húzni:
Pcosβ=mgsinα+μ(mgcosα-Psinβ).
Ebből kiszámítva az egyensúlyhoz szükséges erőt:
P=mg⋅sinα+μcosαcosβ+μsinβ.

Szépen alakítható át ez az eredmény, ha figyelembe vesszük, hogy ε súrlódási határszög tangense a súrlódási együttható: μ=tgε. Ezt behelyettesítve és a törtet cosε-nal bővítve, goniometriai azonosságokkal átalakítva:
P=mg⋅sin(α+ε)cos(β-ε).(2)

Keressük ismét az egyensúlyozáshoz alkalmas P erők végpontjainak mértani helyét. P erő akkor a legkisebb, ha nevezője a legnagyobb, vagyis 1; ez akkor következik be, ha β-ε=0, vagyis β=ε. β szög csak a nevezőben szerepel. Tehát akkor van a legkisebb húzóerőre szükség, ha a kötél akkora pozitív szöget alkot a lejtővel, amennyi a súrlódási határszög. Ez az erő a 6. ábrán AC, nagysága mgsin(α+ε). (2) képletünk szerint a tetszőleges irányú AP erőt a maximális erőből úgy kapjuk, hogy elosztjuk cos(β-ε)-nal. Ez azt jelenti, hogy ACX∢ derékszög és a keresett mértani hely az AC-re C-ben emelt merőleges. Ennek ismerete igen megkönnyíti az áttekintést.
Az AX távolságot úgy kapjuk meg, hogy AC=mgsin(α+ε) befogót elosztjuk AXC∢ sinusával. Ez a szög α+ε. Tehát az AX távolság súrlódásos esetben is mg súllyal egyenlő, mint a súrlódás nélküli esetben. Tehát a β szög számára megengedett szögtartomány a pozitív irányban most is 90∘-α-ig terjed, különben P erő leemelné a tárgyat a lejtőről. Negatív irányban β most 0∘-tól 90∘-ε-ig terjedhet. A negatív irányban 90∘ és 90∘-ε közötti szögtartományban hiába alkalmazunk akármilyen nagy erőt; amelynek még volna lejtő irányú összetevője, mert ez az erő annyira odaszorítja a tárgyat a lejtőhöz, hogy a megnövekedett súrlódási erő teszi lehetetlenné a felhúzást. A lejtő önzáró, mint a fába behajtott facsavar vagy a lemezeket összetartó anyáscsavar.
 
 
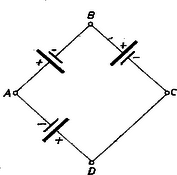7. ábra
 

3. Három 2volt elektromotoros erejű és 1ohm belső ellenállású elemet a 7. ábra szerint kapcsolunk. Mekkora az egyes csúcspontok feszültsége az A ponthoz képest a) az ábra szerinti kapcsolás esetén? b) ha az A-D ágban levő elem belső ellenállása 3ohmra növekszik? c) ha a C-D ágba 2ohmos ellenállást kapcsolunk? d) ha a B és D pontok közé 0,5ohmos ellenállást kapcsolunk? e) ha a B és D pontokat rövidre zárjuk?
 
 
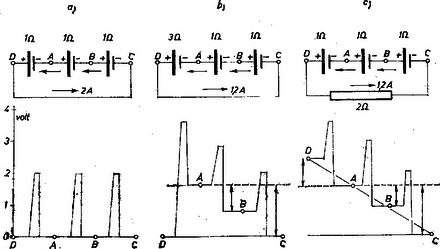8. ábra
 

Megoldás. A galvánelemek tulajdonsága, hogy a rajtuk átmenő áram irányában haladva a lemezek közötti feszültségkülönbség annyit ugrik, amennyi az elem elektromotoros ereje, emellett annyit esik, mint az elem belső ellenállásának és az áramerősségnek a szorzata. E két feszültségváltozás algebrai összege mérhető a lemezek között. 8. ábránk egy sorban egymás mellé rajzolva mutatja az elemeket. a) esetben az összes elektromotoros erő 3⋅2=6 volt, az összes ellenállás 3⋅1=3 ohm, tehát az áramerősség 6:3=2 amper. Induljunk el C-ből. Az első elem 2 volttal emelné a feszültségkülönbséget elektromotoros ereje folytán, de belső ellenállásán 2⋅1=2 voltot esik is, tehát a lemezek között nem észlelünk feszültségkülönbséget. Ugyanígy van ez a másik két elemnél is. A, B, C, D pontok egyező feszültségen vannak, bármely két pont között mérve a feszültségkülönbség 0.
b) esetben az összes elektromotoros erő 3⋅2=6 volt, az összes ellenállás 3+1+1=5 ohm, tehát az áramerősség 6:5=1,2 amper. C-ből B-be haladva az emelkedés 2 volt, a süllyedés 1⋅1,2=1,2 volt, tehát B0,8 volttal pozitívabb, mint C. Pontosan ez történik B-ből A-ba haladva. A-tól D felé haladva az emelkedés 2 volt, az esés 3⋅1,2=3,6 volt, végeredményben D pont 1,6 volttal negatívabb, mint A. A feladat szerint a feszültségeket A ponthoz kell viszonyítani, tehát B0,8 volttal, C és D1,6 volttal negatívabb, mint A.
A c) kérdésben ugyanazok az elemek szerepelnek, mint a)-ban, de a telep nincs rövidre zárva, hanem véges ellenálláson van. Az összes elektromotoros erő most is 6 volt, az összes ellenállás 3⋅1+2=5 ohm és az áramerősség ismét 6:5=1,2 amper. C-től B-ig 2 volt emelkedéshez 1⋅1,2=1,2 volt esés tartozik, tehát B0,8 volttal pozitívabb, mint C. Ugyanez van B és A, valamint A és D között, D és C között a külső 2 ohmos ellenálláson átfolyó 1,2 amper 2⋅1,2=2,4 voltos feszültségesést jelent, amivel visszaértünk C feszültségéhez. A-hoz viszonyítva D0,8 volttal pozitívabb, B0,8 volttal és C1,6 volttal negatívabb.
A d) és e) kérdésekben feltehetően az a) kérdés összeállításából kell kiindulni. Ebben az esetben B és D között nincs feszültségkülönbség, tehát közéjük bármit kapcsolva ezen nem megy át áram és minden feszültség egyenlő marad, mint a) esetben.