1. Kérdés: A nyáron felvételiztem az Eötvös Loránd Tudományegyetemen. A következő feladatot kaptam. Egy $2\text{kg}$-os deszkalapon egy $1\text{kg}$-os deszkalap fekszik. Legfeljebb mekkora $P$ erővel gyorsíthatom a $2\text{kg}$-os tömegű deszkát, hogy az $1\text{kg}$-os ne mozduljon el rajta, ha a nyugalmi súrlódási együttható a két test között, továbbá a súrlódási együttható a deszka és az asztal között $0\mathrm{,}2$ ?
A feladatot nem tudtam megoldani. Majdnem mindenkinek rossz lett a megoldása, kivéve egy fiút, aki ,,tehetetlenségi erők''-ről beszélt, melyek ,,mozgó koordinátarendszerekben'' fellépnek. Szükségesek-e e fogalmak, vagy a feladat megoldható a középiskolai tananyaggal is ?
 (Horváth Lajos)

(m1+m2)gμ1 súrlódási erő is, így

amiből
${\displaystyle \begin{array}{c}\hfill {\displaystyle P=\left(m_1+m_2\right)\left(a+g{\mu }_1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle P=3\text{kg}\cdot \left(2+0\mathrm{,}2\cdot 10\right){\text{m/sec}}^2=12\text{N}\mathrm{.}}\hfill \end{array}}$


Elemezzük még a következő feladatot.

 

 

Az ábrán látható kiskocsi vízszintes irányban $a$ gyorsulással mozog. Milyen irányban áll a kiskocsin levő $m$ tömegű testet tartó fonal ?
Ahhoz, hogy a kiskocsin levő $m$ tömegű test a kiskocsival együtt vízszintes irányban $a$ gyorsulással mozogjon, kell, hogy ugyanilyen irányú $P=ma$ erő legyen az $m$ tömegre ható erők eredője. Az $m$ tömegre csak a súlya, $mg$ és a fonál $F$ feszítőereje hat. Kell tehát, hogy $ma$ e két erő eredője legyen. Az erők vektoriális összeadásából nyerjük, hogy $F=\sqrt[]{{\left(mg\right)}^2+{\left(ma\right)}^2}$. Az erőnek a függőlegessel bezárt $\alpha$ szögére igaz: $\text{tg}\alpha =ma/mg$, azaz $\text{tg}\alpha =a/g$.
Az $F$ erőt a fonál szolgáltatja, így a fonálnak is ebben az irányban kell állnia. Látható, hogy ha $a=0$, tehát a kiskocsi áll vagy egyenesvonalú egyenletes mozgást végez, akkor a fonál függőlegesen lóg, mivel $\alpha =0$.
E két feladatban tehát nincs szükség ,,tehetetlenségi erők'' vagy ,,mozgó koordinátarendszerek'' bevezetésére. Meg kell azonban jegyeznünk, hogy ezek segítségével sok esetben könnyebbé válik a feladat megoldása, de minden feladat megoldható nélkülük is.
1. ${30}^{\circ }$-os lejtőn $2{\text{m/sec}}^2$ gyorsulással felfelé gyorsul egy kiskocsi. Mekkora és milyen irányú erővel kell tartani a kiskocsin levő $1$ kg-os tömeget, hogy a kiskocsival együtt mozogjon, ha a tömeg és a kocsi között nincs súrlódás ?
2. Mekkora erő feszíti azt a kötelet, mellyel $10$ kg tömegű vödröt $3{\text{m/sec}}^2$ gyorsulással függőlegesen felfelé gyorsítunk, ha a kötél tömegét elhanyagoljuk ?
Poór István

 

2. Kérdés. Feladatokban gyakran számítjuk vezetők mágneses terét. Mit kell tudnunk Biot és Savart erre vonatkozó törvényéről ?
 (Kislaki Zoltán)

 

Felelet. Oersted dán fizikus észlelte először 1820-ban, hogy vékony platinadróton átfutó áram kitéríti a mágnestűt. Még ugyanebben az évben Ampére állapította meg azt a törvényszerűséget, amely kapcsolatba hozza a mágnestű kitérését az áram irányával. Az áram erőssége és a mágneses térerősség közötti összefüggésre ugyanebben az időben talált rá a két francia fizikus, Biot és Savart. Törvényüket a ma használatos formában Laplace írta fel először.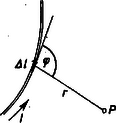

 

 

1. ábra

 

A Biot‐Savart törvény elsősorban igen vékony vezetőkre vonatkozik, amelyekben állandó $\left(I\right)$ erősségű (stacionárius) áram folyik. Azt mondja ki, hogy ha a vezetőnek egy igen kicsi (egyenesdarabnak tekinthető) $\Delta l$ szakaszát tekintjük, akkor az $I$ áram által keltett mágneses térerősség nagysága a $P$ pontban

$\begin{array}{c}{\displaystyle \Delta H=\frac{1}{4\pi }\frac{I\cdot \Delta l\cdot \text{sin}\phi }{r^2}\mathrm{,}}\end{array}$

ahol $r$ az elemi vezetőhossz távolsága a $P$-től, $\phi$ pedig a szög, amelyet az áram iránya $r$-rel zár be. A tér irányát az ismert jobbkéz-szabály adja meg és a tér-erősség értékét A/m-ben kapjuk, ha az áramerősséget amperben, a távolságot méterben adjuk meg.
Első látásra feltűnik a hasonlóság a Newton-féle gravitációs törvénnyel, vagy a Coulomb-féle törvényekkel. Jellegzetesen távolhatási törvény, mint ezek, szemben az elektromágneses térre vonatkozó Maxwell-féle törvényekkel, vagy a gravitáció esetén az általános relativitáselmélettel. De amint az utóbbi tartalmazza a Newton-féle törvényt, vagy a Maxwell-elmélet a Coulomb-törvényt, ugyanúgy a Maxwell-féle térelméletből bizonyos feltételek mellett kiadódik a Biot‐Savart törvény is.
Jelentősége annyiban nagy, hogy segítségével bármilyen alakú vékony vezetőben folyó áram mágneses térerőssége meghatározható. Az egyes áramelemek által keltett térerősségeket kell vektorilag összegezni a paralelogramma-tétel szerint. Természetesen ez csak igen egyszerű vezetők esetén lehetséges így. Integrálszámítás segítségével azonban elvileg minden vezetőre elvégezhető a számítás.
Nézzünk néhány egyszerű példát, ahol a számítás nem ütközik nehézségbe.

 

1. Kör alakú vezetőben folyó állandó erősségű áram mágneses tere a kör középpontjában.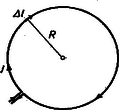

 

 

2. ábra

 

Az elemi hosszúságú áramdarab mágneses térerőssége:

$\begin{array}{c}{\displaystyle \Delta H=\frac{1}{2\pi }\frac{I\cdot \Delta l}{R^2}\mathrm{,}}\end{array}$

mivel $\phi ={90}^{\circ }$. A tér nyilván merőleges a rajz síkjára és befelé mutat. Mivel a kör mentén minden $\Delta l$ hosszra ugyanaz a térerősség nagyság és irány szerint, azért az eredő

$\begin{array}{c}{\displaystyle H=\frac{I}{4\pi R^2}\sum \Delta l\mathrm{.}}\end{array}$

De

$\begin{array}{c}{\displaystyle \sum \Delta l=2R\pi \mathrm{,}\text{s így}H=\frac{I}{2R}\mathrm{.}}\end{array}$

Ha nem egy menet fut, hanem $N$ egymás mellett oly szorosan, hogy vékony csövet képeznek, akkor

$\begin{array}{c}{\displaystyle H=\frac{IN}{2R}\mathrm{.}}\end{array}$

2. Hasonlóképpen elvégezhető a számítás a körvezető síkjára merőleges, a középpontra állított egyenes mentén $x$ távolságra.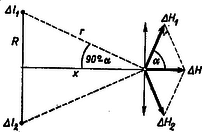

 

 

3. ábra

 

 

 

4. ábra

 

A kör kerületének $\Delta l_1$ szakaszára fennáll:

$\begin{array}{c}{\displaystyle \Delta H_1=\frac{I}{4\pi }\cdot \frac{\Delta l_1}{r^2}=\frac{I\cdot \Delta l_1}{4\pi \left(R^2+x^2\right)}\mathrm{,}}\end{array}$

mert $\phi ={90}^{\circ }$. A tér iránya pedig merőleges $r$-re és a rajzban felfelé mutat. Vegyük most az ugyanazon átmérő másik végén fekvő $\Delta l_2$ szakaszt. A térerősség nagysága megegyezik az előbbiével, de iránya lefelé mutat, vagyis a két vektor $x$-re merőleges komponensei kiegyenlítik egymást, míg az $x$ irányába esők összeadódnak.
A két elemi áramszakasz által keltett térerősség tehát

$\begin{array}{c}{\displaystyle \Delta H\text{'}=2\cdot \Delta H_1\text{cos}\alpha =\frac{I}{2\pi }\cdot \frac{\Delta l_1}{R^2+x^2}\text{cos}\alpha \mathrm{.}}\end{array}$

De $\text{cos}\alpha =\text{sin}\left({90}^{\circ }-\alpha \right)=\frac{R}{\sqrt[]{R^2+x^2}}$,
s így

$\begin{array}{c}{\displaystyle \Delta H\text{'}=\frac{IR}{2\pi }\frac{\Delta l_1}{{\left(R^2+x^2\right)}^{3/2}}\mathrm{.}}\end{array}$

Ha most a $\Delta l_1$-eket összegezzük a félkörre és a vesszős jelölést elhagyjuk, nyerjük:

$\begin{array}{c}{\displaystyle H=\frac{1}{2}\frac{I\cdot R^2}{{\left(R^2+x^2\right)}^{3/2}}\mathrm{.}}\end{array}$

Ezt a képletet kell használni a szolenoid mágneses terének kiszámításához, amely azonban csak az integrálszámítás alkalmazásával végezhető el.
3. Felsőbb analízis nélkül eredményt lehet elérni az $\text{570.}$ feladat esetén is. A számítás menete a következő.
Először csak a félgömbre tekercselt $N$ menet esetében végezzük el. Tekintsük a menetek síkjára merőleges főkör-metszetet, amely $R$ sugarú félkör. Osszuk fel az $R$-et $n$ számú (kicsiny) $\Delta x$ hosszúságú egyenlő részre. A $\nu$-edik szakaszhoz tartozzék a $\Delta S$ hosszúságú egyenesnek vehető körív.

 

 

5. ábra

 

Mivel a negyedkörön egységnyi távolságra

$\begin{array}{c}{\displaystyle \frac{N}{R\pi /2}=\frac{2N}{R\pi }}\end{array}$

menet esik, a $\Delta S_{\nu }$-n $\frac{2N}{R\pi }\Delta S_{\nu }$ menet található. De nyilván

$\begin{array}{c}{\displaystyle \Delta S_{\nu }\approx \frac{\Delta x}{\text{sin}{\alpha }_{\nu }}=\frac{R}{{\varrho }_{\nu }}\Delta x}\end{array}$

(ekkor relative kis hibát követünk el, ha $n$ elég nagy) s így a $\Delta x=\frac{R}{n}$ vastagságú gömbrétegben a menetek száma $\frac{2N}{\pi }\cdot \frac{x}{{\varrho }_{\nu }}$. Ezért az ezek által keltett térerősség a középpontban közelítőleg

$\begin{array}{c}{\displaystyle \Delta H_{\nu }\approx \frac{I}{2}\frac{{\varrho }_{\nu }^2}{[{\varrho }_{\nu }^2+{\left(\nu \Delta x^2\right]}^{3/2}}\cdot \frac{2N}{\pi }\frac{\Delta x}{{\varrho }_{\nu }}=\frac{I\cdot N}{R^3\pi }{\varrho }_{\nu }\cdot \Delta x\mathrm{,}}\end{array}$

mert

$\begin{array}{c}{\displaystyle {\varrho }_{\nu }^2=R^2-{\left(\nu \Delta x\right)}^2\mathrm{.}}\end{array}$

Tehát

$\begin{array}{c}{\displaystyle H\approx \frac{IN}{R^3\pi }\sum _{\nu =1}^n{\varrho }_{\nu }\Delta x\mathrm{.}}\end{array}$

Minthogy azonban ${\varrho }_{\nu }\Delta x$ a ${\varrho }_{\nu }$ magasságú $\Delta x$ alapú téglalap területe, azért az összegezés $\nu$ szerint a $\Delta x$ alaphosszú téglalapok összterületét adja, amely ha $N$ elég nagy és a nála kisebb $n$ is elég nagy, jól megközelíti a negyedkörlap területét, tehát

$\begin{array}{c}{\displaystyle H\approx \frac{I\cdot N}{4R}\mathrm{.}}\end{array}$

Ez az eredmény egyezik azzal, amelyet az analízis módszere nyújt. Sőt, számításunk menete pontosan fedi az analízis módszerét. Ha az egész gömböt tekercseljük körül, akkor a középpontban nyilván kétszer akkora lesz a térerősség nagysága.
 Dózsa Márton