Cím: 1965. évi Eötvös Loránd Fizikaverseny
Füzet: 1966/február, 81 - 84. oldal  PDF  |  MathML 
Témakör(ök): Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1965. október 23-án rendezte fizikai versenyét az 1965. évben érettségizettek számára. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

 

1. S=20 méter hosszú, súlyos, hajlékony kötél egy kisméretű, súrlódás nélküli csigán van átvetve úgy, hogy az egyik oldalon s0=12 méter hosszú darabja lóg le. A kötelet elengedtük. Mennyi a kötél sebessége akkor, amikor az alsó kötélvég
a) 16 méterre,
b) 40 méterre van a csiga alatt? g=1000cm/sec2.
 

 
 
1. ábra
 

Megoldás. Keressük a sebességet, mint a hely függvényét: legegyszerűbb, ha a mechanikai energiamegmaradás törvényét alkalmazzuk. Ha a kötél lelógó hosszabb része s0, akkor rövidebb része S-s0=s00 (1. ábra). Egy későbbi állapotban a kötél alsó vége s távolságnyira van a csiga alatt. Induláskor a baloldali kötélvég A-ban, a jobboldali B-ben van; amikor a kötél alsó vége s távolságnyira, D-be jutott, akkor felső vége C-be került. Lényegében az történt, hogy a kötél AC=BD=s-s0 hosszúságú darabja AD=s-s00 magasságból leesett. Ha a kötél egységnyi hosszúságú darabját egységnyi tömegűnek vesszük, akkor a helyzeti energia csökkenése mgh=(s-s0)g(s-s00). Ez egyenlő az S tömegű kötél Sv2/2 mozgási energiájával:
Sv22=(s-s0)g(s-s00).
Innen a keresett sebesség:
v=2g⋅(s-s0)⋅(s-s00)S.
Ez a sebességképlet addig érvényes, amíg a kötél még nem csúszott le a csigáról, vagyis amíg s0<s<S. Feladatunk számadataival az a) kérdésre ezt a választ kapjuk: v=32=42=5,66  m/sec.
A kötél mozgása közben a gyorsítandó tömeg állandó marad, viszont a gyorsító erő (a jobboldali kötéltöbblet) s lineáris függvényeként növekszik. Ezért ugyanezt az eredményt kapjuk, ha az egyenletesen gyorsuló mozgás v=2as képletével dolgozunk, de a gyorsulás helyébe a kezdeti és végső gyorsulások számtani középértékét helyettesítjük.
Feladatunk b) kérdésében a kötél már teljesen elhagyta a csigát. Eljárhatunk úgy, hogy kiszámítjuk az s=S=20 méterhez tartozó sebességet előbbi módszerünkkel, azután ezzel mint kezdősebességgel függőleges lefelé hajítást számolunk a 40 méteres mélység eléréséig. De egyszerűbb, ha most is az energia elvet alkalmazzuk. A súlypont mélysége a csiga alatt induláskor:
[s02⋅s0+s002⋅s00]:S=S2-2s0(S-s0)2S.
A súlypont mélysége akkor, amikor az alsó kötélvég s mélységben van: s-S2, eközben a súlypont süllyedése:
s-S2-S2-2s0(S-s0)2S=s-S+s0(S-s0)S.
Ezt a távolságot szorozzuk Sg-vel és egyenlővé tesszük Sv2/2-vel, így kapjuk a kötél sebességét:
v=2g[(s-S)+s0(S-s0)S].
Ez a képlet s>S esetében érvényes. Feladatunk számadataival v=496=431=22,27m/sec.
 

2. Hat kör alakú vezető fémlemezt helyezünk el egymás mellé, párhuzamosan. A szomszédosak közötti d távolság egyenlő és kicsiny a lemezek sugarához képest. A lemezek sugara váltakozva R és 2R. A lemezek középpontjai a síkjaikra merőleges egyenesen vannak. Kapcsoljuk össze a lemezeket úgy, hogy a keletkező kondenzátor kapacitása maximális legyen! Mekkora ez a kapacitás? Hogyan helyezkednek el a töltések a lemezeken?
 Károlyházi Frigyes
 
 
2. ábra
 

Megoldás. Tekintettel arra, hogy a lemezek átmérője távolságukhoz képest nagy, a lemezek szélén keletkező szórt térrel nem kell törődnünk, csak a lemezek közötti homogén térrel, és alkalmazhatjuk azt a törvényt, hogy a kapacitás egyenesen arányos a szemben álló felületekkel és fordítva arányos távolságukkal: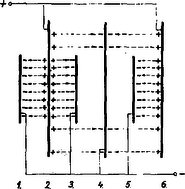
C=k⋅Fd.
(Ha C kapacitást faradban, F területet cm2-ben és d távolságot cm-ben mérjük, akkor az arányossági szorzó k=1/4π⋅9⋅1011).
 
 
3. ábra
 

Tekintsük külön azokat a kondenzátorokat, amelyeket a πR2 területű, d távolságú, πR2/d kapacitású kis körök és a π(2R)2-πR2=3πR2 területű, 2d távolságú, 3πR2/2d kapacitású körgyűrűk alkotnak. Olyan elrendezést keresünk, amelynél minél több tér van kitöltve erővonalakkal, vagyis elektromos térrel. Ami a körgyűrűket illeti, a legjobb, ha a két szélsőt kötjük az egyik pólushoz és a középsőt a másikhoz (3. ábra). Ha két szomszédosat kötnénk egyező pólushoz, ezek között nem volna tér, csak a másik kettő között és a kapacitás kevesebb volna. Ha azt akarjuk, hogy az 1. számú kis kör is szerepeljen, akkor feltétlenül a 2. számú nagy lemezzel ellentétes (vagyis a 4. számú nagy lemezzel egyező) pólushoz kell kötnünk. A 3. és 5. számú kis lemezeket bármelyik pólushoz köthetjük, valamelyik oldalukon biztosan ellentétes feszültségű lemez a szomszédjuk, így kondenzátorként szerepelhetnek.
Összegezve: a teljes kapacitás párhuzamosan kapcsolt három kis körből és két körgyűrűből tevődik össze:
C=3⋅πR2d+2⋅3πR22d=6⋅πR2d,
vagyis a teljes kapacitás a kiskörös kondenzátor kapacitásának 6-szorosa. (Valamennyi kapacitásképlethez hozzátartozik k arányossági szorzó.)
Felmerül a kérdés, nem nyernénk-e kapacitásban, ha a 3‐4. és 4‐5. közötti területeket is kitöltenénk elektromos térrel. Ha a 4. számú nagy lemezt is a pozitív pólushoz kötnénk, nyernénk két kis kört, de elveszítenénk két körgyűrűt. Mivel a gyűrű kapacitása 50%-kal több, mint a kis köré, ezzel csak vesztenénk.
A töltések eloszlása a 3. ábrán látható. Mivel a térerősség fordítva arányos a lemeztávolsággal, ezért az erővonalak a körgyűrűk területén fele sűrűségűek. Ugyanez érvényes a felületi töltéssűrűségre is.
 

3. Adva van egy negyedkörben meghajlított vastag üveglemez, amely egyenes részben folytatódik. Mi a feltétele annak, hogy az egyik véglapra merőlegesen beeső fénysugár ne lépjen ki az üveglemez oldalfalain? (Csak a másik véglapon.) Csak a rajz síkjában haladó fénysugarakkal foglalkozzunk.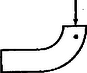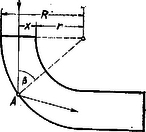
 
 
4. ábra
 

 
 
5. ábra
 

Megoldás. Az üveglemezt 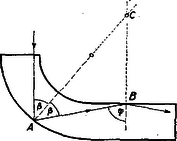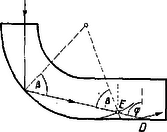R és r rádiuszú hengerfelületek határolják (5. ábra), a fénysugár helyzetét a belső széltől mért x távolság határozza meg. Az üveglemez külső felületét A pontban elérő fénysugár az üvegben marad, ha β szög nagyobb a teljes visszaverődés határszögénél. A teljes visszaverődés határszögének sinusa =1/n (n az üveg törésmutatója), ezért a fény üvegben maradásának feltétele:
sinβ=x+rR≧1n.
A pontban akkor keletkezik a legkisebb β szög, ha x=0, tehát a fény bennmaradásának a feltétele a fenti egyenlőtlenségből:
rR≧1n,
illetve:
Rr≦n,
vagyis a rádiuszok hányadosa ne legyen nagyobb a törésmutatónál. Elég, ha csak a negyedkör alakú üveglemez egyetlen pontjában vizsgáljuk meg a fénysugár viselkedését, mert ha ismét elérné a fénysugár a külső falat, β szög ismét ugyanakkora volna. A negyedkör alakú üveglemez belső falát a fénysugár nem érheti el.
 
 
6. ábra
 

 
 
7. ábra
 

A feladat kérdése szerint meg kell vizsgálni, mi történik az üveglemez egyenes folytatásában. Érje az egyenes folytatásába bejutó fénysugár a felső falat (6. ábra). Az itt szereplő φ beesési szög feltétlenül nagyobb β-nál, mert φ az ABC háromszögnek egy külső, β pedig egy belső szöge. Érheti az egyenes részbe jutó fénysugár az alsó falat (7. ábra). φ szög most is feltétlenül nagyobb β-nál, amint azt az E pontban rajzolt pontozott segédvonal azonnal beláthatóvá teszi. De ha már β is nagyobb volt, mint a teljes visszaverődés határszöge, akkor φ még inkább az. Tehát a negyedkör számára megállapított R/r≦n feltétel biztosítja azt is, hogy a fénysugár nem léphet ki az egyenes folytatás oldalfalain.
 

A verseny eredménye. I. díjat nyert Gnädig Péter (a budapesti Táncsics Mihály gimnáziumban Henter Lászlóné tanítványa) és Juvancz Gábor (a budapesti Fazekas Mihály gimnáziumban Fábián Zoltán és Wiedemann László tanítványa). Dicséretet kapott Szalay Mihály (a budapesti Vörösmarty Mihály gimnáziumban Csekeő István tanítványa) és Várhelyi Gábor (a budapesti Bolyai János gimnáziumban Münster Tiborné tanítványa). A versenyen kívül résztvevő középiskolai tanulók közül dicséretet kaptak Herényi István (a budapesti I. István gimnázium IV. osztályában Cserép Lajos tanítványa), Lovász László (a budapesti Fazekas Mihály gimnázium IV. osztályában Szalay Béla és Wiedemann László tanítványa) és Tüttő Péter (a budapesti Eötvös József gimnázium IV. osztályában Veres Mihályné tanítványa).