Cím: Az 1966. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása
Szerző(k):  Scharnitzky Viktor 
Füzet: 1966/december, 193 - 196. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy egész együtthatós másodfokú egyenletben az ismeretlent tartalmazó két tag együtthatóinak összege páros, az ismeretlent nem tartalmazó tag pedig páratlan szám. Bizonyítandó, hogy az egyenletnek racionális gyöke csak olyan tört lehet, melynek legegyszerűbb alakjában a nevező páros szám.

 
Megoldás. Legyen a szóban forgó egyenlet
ax2+bx+c=0.
A feladat állítása így fogalmazható: egy olyan p/q tört (p és q egész), amelynek q nevezője páratlan, nem lehet gyöke az egyenletnek.
Helyettesítsünk a bal oldalba p/q-t és hozzunk közös nevezőre. Így a
[p(ap+bq)+cq2]/q2
törtet kapjuk. Ha q páratlan, akkor a számláló második tagja páratlan, az első viszont páros, mert vagy p páros, vagy ha p páratlan, akkor ap+bq=(a+b)p+b(q-p), és itt a+b és q-p páros, tehát a mondott tag értéke is az. Így a számláló páratlan, tehát nem lehet 0, és vele együtt a tört sem. Ezt akartuk bizonyítani.
 
Megjegyzések. 1. Az utolsó átalakításból az is látható, hogy ha p/q nem egyszerűsíthető tört, és gyöke az egyenletnek, és q páros, akkor b-nek (s így a-nak is) párosnak kell lennie; tehát ha egy egész együtthatós másodfokú egyenlet együtthatói páratlanok, akkor nincs racionális gyöke.*
2. A 4x2-16x+7=0 egyenlet pl., amelynek gyökei 1/2 és 7/2, mutatja, hogy a feladat feltételei mellett lehet racionális gyöke az egyenletnek.
3. A feladat állítása a következőképpen általánosítható: Ha egy n-ed fokú egész együtthatós egyenletben (n természetes szám) az ismeretlent tartalmazó tagok együtthatóinak összege páros, az ismeretlent nem tartalmazó tag pedig páratlan, akkor az egyenlet racionális gyöke csak olyan tört lehet, amelynek legegyszerűbb alakjában a nevező páros. A tétel a fenti megoldáshoz hasonlóan bizonyítható.
 
2. feladat. Szerkesszünk adott körbe olyan trapézt, melybe kör írható, és amelynek egyik oldala a körnek átmérője.
 
Megoldás. A megszerkesztendő ABCD trapéz egyenlő szárú, mert húrtrapéz, és szárai a hosszabb párhuzamos oldal szemben levő végpontjából mindenesetre hegyes szögben látszanak, így kisebbek a kör átmérőjénél. A trapéznak a kör átmérőjével egyenlő AB oldala tehát a hosszabb párhuzamos oldal.
 
 
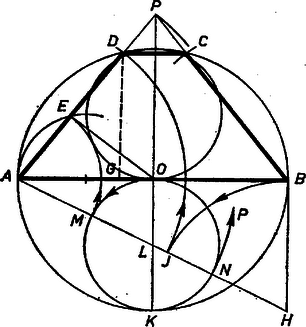1. ábra
 

A szár hosszát számítással határozzuk meg. Legyen AB=1, AD=BC=x, D vetülete az AB oldalon G (1. ábra). Az ABD háromszög Thalész tétele alapján derékszögű, így az ismert mértani középarányos tétel szerint AD2=AB⋅AG, azaz AG=x2. Ezért DC=AB-2AG=1-2x2. Mivel továbbá a trapézba kör írható, azért AD+BC=AB+DC, vagyis
2x=1+(1-2x2),(1)
aminek pozitív gyöke
x=52-12.

Ennek alapján a szerkesztés a következő. Az adott kör O középpontján át tetszés szerint felvett AB átmérő B végpontjában meghúzzuk az érintőt, felmérjük rá a BH=BO=1/2 szakaszt, ekkor AH=5/2. Az AH szakaszt metsszük a H körül HB sugárral írt körrel J-ben, ekkor AJ=x. Végül az A és B körül AJ sugárral írt körívvel az adott körből kimetsszük a D, illetőleg C csúcsot.
Így a csúcsok a körön vannak, másrészt teljesül (1) is, ezért a trapézba érintő kör írható, tehát megfelel a követelményeknek.
 
Megjegyzés. A fenti szerkesztést felére kicsinyítve végezhetjük el, a kör AB-re merőleges sugarai egyike, OK fölé kört írva. Ennek középpontját L-lel, AL-lel való metszéspontjait M-mel és N-nel jelölve (AM<AN) AM=AJ/2, ennek alapján az AO átmérőjü Thalész körből kimetszhetjük az AD oldal E felezőpontját.
Az N metszéspont alapján viszont a szárak P metszéspontját jelölhetjük ki a trapéz szimmetriatengelyén. Ugyanis OE, mint az OAD egyenlő szárú háromszög magassága, merőleges AP-re, így a PAO derékszögű háromszögből
AP=AO2AE=14⋅AE=14⋅AM=15-1=54+14=AL+LN=AN.

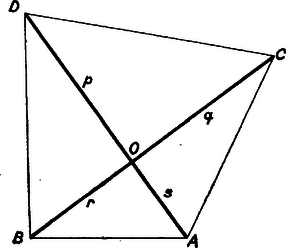
3. feladat. Négy adott szakasz kezdőpontja közös. A szakaszok milyen (egy síkban való) elhelyezése esetén lesz a végpontjaikkal, mint csúcsokkal meghatározott négyszög területe a legnagyobb?
 
 
2. ábra
 

I. megoldás. Legyen az adott szakaszok közös kezdőpontja O, végpontjaik egy bizonyos helyzetben A, B, C, D, a betűzést úgy választva, hogy ABCD ne hurkolt négyszöget adjon. Ennek területe, mint ismeretes (2. ábra)
t=12⋅AC⋅BD⋅sinφ,(2)
ahol φ az AC és AD átlók által bezárt szög.
A szakaszok kölcsönös helyzetét változtatva mindig fennáll
AC≤AO+OC,BD≤BO+OD,(0≤)sinφ≤1,
tehát
t≤12(AO+OC)(BO+OD).


Itt az egyenlőség teljesül, (2) tényezői (egymástól függetlenül) elérik legnagyobb értéküket, ha az OA és OC, valamint OB és OD szakaszok egymás meghosszabbításába esnek ‐ más szóval, ha O az AC és BD átlók metszéspontjává válik ‐, és ha még φ=90∘, vagyis az átlók merőlegesek egymásra. Ekkor t legnagyobb értéke csak a szakaszok hosszától és azok két párba rendezésétől függ.
A 4 szakasz 2 párba állítása háromféleképpen lehetséges, mert az elsőnek kiválasztott szakasz meghosszabbításába a további 3 bármelyikét állíthatjuk, és ezután mindig a maradó 2 szakasz alkotja a másik párt. Legyen a 4 szakasz hossza p, q, r, s úgy, hogy p≥q≥r≥s(>0), így a kétszeres terület legnagyobb értéke a következő 3 szorzat valamelyike:
2t1=(p+q)(r+s),2t2=(p+r)(q+s),2t3=(p+s)(q+r).
A harmadikból az elsőt, majd a másodikat kivonva a különbség így alakítható:
2(t3-t1)=(p-r)(q-s),2(t3-t2)=(p-q)(r-s).
Ezek egyike sem negatív, tehát t3≥t1, t3≥t2, így p-nek s-sel ‐ vagyis a leghosszabb szakasznak a legrövidebbel ‐ egy átlóba állítása esetén kapunk legnagyobb területű négyszöget (3. ábra).
 
 
3. ábra
 

 
II. megoldás. A fentebbi jelölésekkel az OAB, OBC, OCD és ODA háromszög területe külön-külön akkor a legnagyobb, ha O-ból kiinduló két oldaluk merőleges egymásra. Ez a 4 feltétel egyidejűen teljesíthető úgy, hogy a négy háromszög O-nál levő derékszögeivel kitöltjük az O pont körüli 360∘-os szögtartományt, és ekkor az ABCD négyszög területe is a legnagyobb, egyenlő a négy derékszögű háromszög területének összegével. Ebben az elhelyezésben 2‐2 szakasz egymás meghosszabbításába esik, és az ABCD négyszög egy-egy átlóját alkotja.
A szakaszok fenti 3 párosításából akkor kapunk legnagyobb területet, ha az egyik átló a legkisebb és a legnagyobb szakasz összege. Ismeretes ugyanis, hagy két egyenlő kerületű téglalap közül annak nagyobb a területe, amelyikben az oldalak különbsége (abszolút értékben) kisebb. Más szóval, ha két (két-tényezős) szorzatban a tényezők összege ugyanakkora, akkor az a szorzat nagyobb, amelyikben a tényezők kevesebbel térnek el egymástól. Esetünkben a két tényező a 4 adott szakaszból alkotott két páros összeg, és ezek eltérése akkor a legkisebb, ha a legkisebb szakaszt a legnagyobbikkal állítjuk párba.
 Scharnitzky Viktor
*Ennek bizonyítása volt az 1961. évi Országos Középiskolai Tanulmányi Verseny II. fordulójának 1. feladata, lásd a megoldást K.M.L. 24. (1962) 1‐2. o.