Cím: Az 1966. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, kezdők versenye, az általános verseny és a speciális osztályok feladatai
Szerző(k):  Bakos Tibor ,  Fried Ervin ,  Tusnády Gábor 
Füzet: 1966/november, 97 - 103. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Kezdők versenye (az általános verseny és a speciális matematikai
osztályok versenye)

 
Az általános és a matematikai osztályok első feladata csak az egyenletrendszer állandóiban különbözött, ezért együtt fogjuk ezeket tárgyalni.
 
1. feladat. Oldjuk meg a következő egyenletrendszert:
xyx+y=1a,yzy+z=1b,zuz+u-1c=0,xyzux+y+z+u=1d,(*)


ahol a=1,b=2,c=-1,d=1 (általános verseny),
ill. a=1,b=3,c=-2,d=1 (matematikai osztályok versenye).
 
Megoldás. Az utolsó egyenletnek csak olyan megoldása lehet, amelyikben egyik ismeretlen sem 0, így létezik a reciprokuk. A harmadik egyenletben az állandót a jobb oldalra víve, majd az első három egyenlet reciprokát véve, elsőfokú egyenletrendszert kapunk az ismeretlenek reciprokaira:
1x+1y=a,1y+1z=b,1z+1u=c.
Innen bármely három ismeretlen kifejezhető a negyedikkel és a negyedik egyenletbe helyettesítve egyismeretlenes egyenletet kapunk. Célszerű lesz azonban először annak is a reciprokát venni és x-et és y-t, valamint z-t és u-t együtt tartva az első és a harmadik egyenlet felhasználásával átalakítani az egyenletet:
x+y+z+uxyzu=x+yxy⋅1zu+z+uzu⋅1xy=a1zu+c1xy=d.
Most kifejezzük 1y-nal a többi ismeretlen reciprokát és az utolsó egyenletbe helyettesítjük:
1x=a-1y,1z=b-1y,1u=c-1z=c-b+1y;a(b-1y)(c-b+1y)+c(a-1y)1y=d.


Ebből rendezéssel a következő egyenletet kapjuk 1y-ra:
(a+c)(1y)2-2ab(1y)+ab2-abc+d=0.(1)

Az első konstans értékek mellett elsőfokú egyenletet kapunk:
-4y+7=0,1y=74,így1x=-34,1z=14,1u=-54


és az egyenletrendszer megoldása
x=-43,y=47,z=4,u=-45.
Ez valóban megoldás, mert x+y, y+z, z+u  és x+y+z+u egyike sem 0, és így minden végzett átalakítás megfordítható.
A matematikai osztályok feladata esetében (1) így alakul: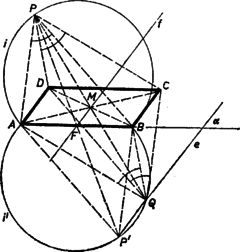
(1y)2+6⋅1y-16=0.
Mindkét oldalhoz 25-öt adva
(1y+3)2=25,
amiből a következő két lehetőség adódik: 1y=2, és 1y=-8. Ennek megfelelően a többi ismeretlen reciprokára is két értéket kapunk:
1y=2esetén1x=-1,1z=1és1u=-3;1y=8esetén1x=9,1z=11és1u=-13.
Innen a következő két gyökrendszer adódik:
x=-1,y=12,z=1ésu=-13,x=19,y=-18,z=111ésu=-113.
Ismét mindkét számnégyes megoldása az egyenletrendszernek.
 
A két versenyág 2. feladata közös volt.
 
2. feladat. Adott egy paralelogramma két szomszédos csúcsa és egy szöge, továbbá adott a síknak egy olyan pontja, amelyből az adott csúcsok közti oldal és a vele szemben levő oldal egyenlő szögek alatt látszik. Szerkesszük meg a paralelogrammát.
 
I. megoldás. Legyenek a keresett ABCD paralelogramma adott csúcsai A és B. Mivel a paralelogramma egy szöge a többit meghatározza, ezért feltehetjük, hogy az adott szög a DAB∢=α. Végül jelöljük a sík adott pontját ‐ amelyből az AB és CD szakasz egyenlő szög alatt látszik ‐ P-vel.
 
 
1. ábra
 

Ha meg tudjuk szerkeszteni a paralelogramma átlóinak M metszéspontját, ezzel a feladatot megoldottuk, mert C az A-nak és D a B-nek M-re vonatkozó tükörképe (1. ábra). Mivel a paralelogramma M-re szimmetrikus, azért P-nek M-re vonatkozó Q tükörképéből is ugyanakkora szög alatt látszik mind az AB, mind a CD szakasz, mint P-ből. A tükrözésből következik, hogy M a PQ szakasz felezőpontja, ezért elegendő a Q pont megszerkesztése. Q rajta van az AB szakasz fölé rajzolt azon két látókörív valamelyikén, amelyek pontjaiból az AB szakasz ugyanakkora szög alatt látszik, mint P-ből, hiszen Q-ból és P-ből az AB szakasz egyenlő szögben látszik.
Másrészt M-en átmennek a paralelogramma középvonalai. Az AD oldallal párhuzamos f középvonalát azonnal meghúzhatjuk, ez átmegy az AB szakasz F felezőpontján és α szöget zár be az AB egyenessel. Mivel a PQ szakasz felezőpontja rajta van f-en, azért Q-nak rajta kell lennie azon az f-fel párhuzamos e egyenesen, amely a P-nek az f pontjaira vonatkozó tükörképeiből áll. Így Q, mint a fenti két látókörív és az e egyenes közös pontja, megszerkeszthető.
A szerkesztés a következő: vesszük az ABP háromszög körülírt körének P-t tartalmazó AB=i ívét; ez nyilvánvalóan a szóban forgó látókörívek egyike, a másika pedig ennek i' tükörképe F-re. Kimetsszük i'-n P-nek F-re vonatkozó P' tükörképét. P'-n és F-en át megszerkesztjük az AB-vel α szöget bezáró e, illetőleg f egyenest. Az e és az i, i' pár valamelyik (de P'-től különböző) Q közös pontját P-vel összekötő egyenes f-ből kimetszi M-et, végül A és B tükörképe M-re C, ill. D. Az ABCD négyszög megfelel a követelményeknek, mert az utolsó két tükrözés miatt paralelogramma, oldalai párhuzamosak FM-mel, tehát DAB∢=α, végül CPD∢=AQB∢=APB∢, mert Q a P tükörképe M-re. A feladat diszkusszióját a III. megoldás után tárgyaljuk.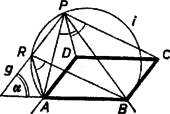
 
Megjegyzés. f és M megszerkesztése el is maradhat. D paralelogrammává egészíti ki a PBQ háromszöget, C pedig a BAD háromszöget. ‐ Így természetesen a bizonyítás is módosul: P' szerkesztése szerint PAP'B paralelogramma, D (új) szerkesztése szerint PBQD szintén, így az APD és P'BQ háromszögben az AP és P'B, továbbá PD és BQ oldalak egy irányban párhuzamosak és egyenlők, tehát az AD és P'Q oldalak is, vagyis DA‖e, DAB∢=α.
 
 
2. ábra
 

II. megoldás. Toljuk el a PCD háromszöget úgy, hogy D csúcsa A-ba kerüljön (2. ábra). Ezáltal C a B-be kerül, P pedig egy olyan R pontba, melyből az AB szakasz ugyanakkora szögben látszik, mint P-ből CD, vagyis mint P-ből AB. R tehát rajta van az előbbi két látókörív valamelyikén.
Másrészt az eltolás közben P az AD-vel párhuzamosan mozgott, így R rajta van a P-n átmenő és az AB egyenessel α szöget bezáró g egyenesen. Ezek alapján R, mint g és a két látókörív közös pontja, megszerkeszthető, D pedig paralelogrammává egészíti ki az ARP háromszöget.
 
III. megoldás. Mindkét fenti megoldásban első lépésként két körív és egy egyenes metszéspontját kerestük meg, ebből kaptuk meg a paralelogramma csúcsait. Az I. megoldásban a metszéspontból előbb a paralelogramma középpontját határoztuk meg, a II. megoldásban a metszéspontból már közvetlenül kaptuk az egyik csúcsot. Most olyan megoldást adunk, melyben a körívek és egy egyenes metszéspontja mindjárt maga az egyik csúcs. Egészítsük ki a BAP háromszöget a T ponttal a BAPT paralelogrammává (3. ábra). Ekkor a CDPT négyszög is paralelogramma, PA és TB, valamint PD és TC is párhuzamosak, ezért és a feltevés miatt
PCT∢=CPD∢=BPA∢=PBT∢,
vagyis C-ből a PT szakasz ugyanakkora szögben látszik, mint B-ből. C tehát rajta van azon két j, j' látókörív valamelyikén, melyeknek pontjaiból a PT szakasz ugyanakkora szögben látszik, mint B-ből. Másrészt C rajta van a B-n átmenő, AB-vel α szöget bezáró h egyenesen is (CBA∢=180∘-α), tehát C e két mértani hely közös pontja.
Kimutatjuk, hogy e közös pontok bármelyike megfelel C-ként ‐ kivéve természetesen B-t. Mivel C rajta van h-n, azért a paralelogramma szögei megfelelők, továbbá PD‖TC. Másrészt C rajta van j és j' valamelyikén, ezért DPC∢=PCT∢=PBT∢=BPA∢, mint állítottuk.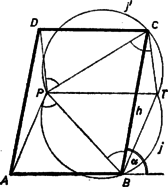
 
 
3. ábra
 

Ezek alapján a szerkesztés a következő: párhuzamost húzunk P-n át AB-vel és B-n át AP-vel, e két egyenes metszéspontja T. Megrajzoljuk a BPT háromszög köré írt kör B-t tartalmazó PT=j ívét és ennek PT-re, való j' tükörképét. Ezután B-n át meghúzzuk azt a h egyenest, amely AB-vel α szöget zár be. Ekkor h-nak j-vel, j'-vel való, B-től különböző közös pontja (e közös pontok bármelyike) adja a paralelogramma C csúcsát.
h-nak mindkét ívvel legfeljebb két közös pontja van, és j-vel mindenesetre közös pontja B, azért a megoldások száma legfeljebb 3. Csak abban az esetben nem kapunk megoldást, ha B a h-nak j-vel egyetlen közös pontja, és itt érintkeznek, j'-vel pedig nincs közös pontja. (*Ha ugyanis h a j-t B-ben metszi, akkor van pontja a j, j' ívekkel határolt idom belsejében, így a kilépési pont megfelel C-ként.)
Ha elejtjük azt az előírást, hogy az adott szög a paralelogramma A-nál levő szöge legyen, akkor h-nak az AB egyenesre való h* tükörképe is tekintetbe veendő. Ekkor a megoldások száma 6, 5, 4, 3, 2 vagy 1 (a 4‐6. ábrákon példákat látunk ilyen helyzetekre, 1 megoldás van az 1‐3. ábrák helyzeteiben is). Kimutatjuk ugyanis, hogy így minden esetben létezik legalább 1 megoldás. (A 4‐6. ábrák 2‐2 felén csak P és T közös. )
 
 
4.ábra5.ábra6.ábra
 

Elég az olyan helyzeteivel foglalkoznunk h*-nak, amelyekben fentebb h nem adott megoldást. Ekkor h* ‐ amennyiben különböző a h-tól ‐ nem érinti, hanem metszi j-t B-ben és a fenti (*) megjegyzés szerint megoldást szolgáltat.

Ha pedig h* egybeesik h-val, akkor α=90∘ (mert α=0∘ nyilvánvalóan nem jön szóba), így h merőleges PT-re, és mivel B-ben érinti j-t, azért a szimmetria miatt B-nek PT-re való tükörképében érinti j'-t, ez a közös pont megoldást ad.
Könnyű belátni, hogy j, j' az I. és II. megoldásban szerepelt i, i' körívpárból AP irányú és nagyságú eltolással áll elő, hogy ugyanez áll fenn h és az I. megoldásbeli e egyenes között, végül hogy a II. megoldásbeli g egyenes az e tükörképe F-re. Ezért a III. megoldásra adott diszkusszió a megfelelő változtatásokkal az I. és II. megoldásra is érvényes.
 
*

 
Az általános verseny 3. feladata: Határozzuk meg a (tízes alapú számrendszerben felírt) ABCC számot, ha
ABCC=(DD-E)⋅100+DD⋅E,
ahol A, B, C, D és E különböző számjegyek.
 
Megoldás. A szereplő többjegyű számokat a következőképpen alakítjuk át:
ABCC=1000⋅A+100⋅B+11⋅C,DD=11⋅D.
Ezeket behelyettesítve rendezzünk úgy, hogy a bal oldalra kerüljenek azok a tagok, amelyekben az egyik tényező 100, a többiek a jobb oldalra:
(10⋅A+B-11⋅D+E)⋅100-11⋅(D⋅E-C),(2)
így a jobb oldalnak is oszthatónak kell lennie 100-zal. Ez csak úgy lehetséges, ha D⋅E-C osztható 100-zal. Mivel D, E és C mindegyike 0 és 9 közé esik, és különbözők, azért D⋅E-C legfeljebb 9⋅8-0=72, és legalább 0⋅1-9=-9. Márpedig -9 és 72 között csak egyetlen 100-zal osztható szám van, mégpedig 0, így D⋅E=C, továbbá (2) bal oldalán is 0-nak kell állnia, ezért a zárójelen belüli kifejezés 0. Írjunk ebben 10⋅A helyett 11⋅A-A-t, és rendezzük át az egyenletet:
B+E-A=11⋅(D-A).
Mivel D és A különbözőek, ezért a jobb oldal, s így a bal oldal is 0-tól különböző szám. Továbbá a jobb oldal osztható 11-gyel, tehát a bal oldal is. Ezek szerint B+E-A11-gyel osztható és 0-tól különböző (egész) szám. Másrészt, mivel B, A és E ugyancsak 0 és 9 közé esnek és A≠0, ezért B+E-A legfeljebb 9+8-1=16, és legalább 0+1-9=-8. Mármost -8 és 16 között 0-tól különböző és 11-gyel osztható szám csak egy van, a 11. Ezért B+E-A=11, amiből D-A=1 adódik.
Eddig tehát a következőket állapítottuk meg:
D⋅E=C,B+E-A=11ésD=A+1.
A harmadik egyenlőségből A-t kifejezve és a másodikba behelyettesítve:
B+E=D+10,
amit átrendezve:
E=D+(10-B).
Mivel B legfeljebb 9, ezért 10-B legalább 1, és így E legalább D+1, más szóval E nagyobb D-nél. Ennek alapján D⋅D kisebb, mint D⋅E, vagyis C, ami legfeljebb 9; azaz D2 kisebb 32-nél, D kisebb 3-nál. Másrészt D=A+1≥2, így D=2, amiből A=1, továbbá
C=2EésB+E=12.

E>D miatt E≥3. Másrészt E≤4, különben C kétjegyű szám lenne. Az E=4 esetben C=B(=8) adódik, ami ismét nem felel meg a számjegyek különbözőségének. Az egyetlen maradó lehetőség E=3, amiből C=6, és B=9.
A jegyek adódott értékei valóban kielégítik a feltételeket:
1966=(22-3)⋅100+22⋅3.

 
A matematikai osztályok versenyének 3. feladata: Keressük meg az olyan hatjegyű négyzetszámokat, amelyeknek első három jegyét letörölve a szám négyzetgyökét kapjuk.
 
Megoldás. Jelöljük a szám négyzetgyökét x-szel. x2 hatjegyű szám, ezért x háromjegyű és x2 első három jegyét letörölve keletkezik, vagyis az x2 utolsó három jegyéből álló szám. Így tehát x2-x=x(x-1) utolsó három jegye 0, osztható 1000-rel. Feladatunk tehát olyan x háromjegyű számok keresése, melyekre x(x-1) osztható 1000=125⋅8-cal.
Vizsgáljuk a 125-tel való oszthatóságot. Mivel x(x-1) osztható 125-tel, ezért osztható 5-tel is. x-nek és x-1-nek legnagyobb közös osztója 1, ezért x és x-1 közül csak egyik lehet 5-tel osztható. Ekkor viszont az 5-tel osztható tényező osztható 125-tel is, így azt kaptuk, hogy x és x-1 egyike osztható 125-tel.
Hasonló okoskodással belátható, hogy a két tényező valamelyike osztható 8-cal. Az azonban nem lehet, hogy ugyanaz a tényező osztható 125-tel és 8-cal, ekkor ugyanis ez a tényező osztható lenne 125⋅8=1000-rel is, tehát legalább négyjegyű szám lenne. Így x és x-1 egyike 125-tel és a másik 8-cal osztható. Olyan többszörösét kell keresnünk a 125-nek, amelyiknek valamelyik szomszédja, vagyis az 1-gyel kisebb vagy 1-gyel nagyobb szám osztható 8-cal. Ez a szomszéd páros is és 4-gyel is osztható, ezért elég 125 páratlan többszöröseivel próbálkozni, ezek: 125, 375, 625 és 875. Szomszédaik közül a 26-ra és 74-re végződők még 4-gyel sem oszthatók, 124 és 876 sem osztható 8-cal, így csak két számpár marad: x=376 és x-1=375, valamint x=625 és x-1=624.
Valóban: 3762=141376 és 6252=390625.
 
 Fried Ervin