Cím: Az 1965. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása
Szerző(k):  Surányi János 
Füzet: 1966/május, 198 - 200. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1965. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása

 
Kezdők (legfeljebb I. osztályosok) versenye

A speciális matematikai osztályok feladatai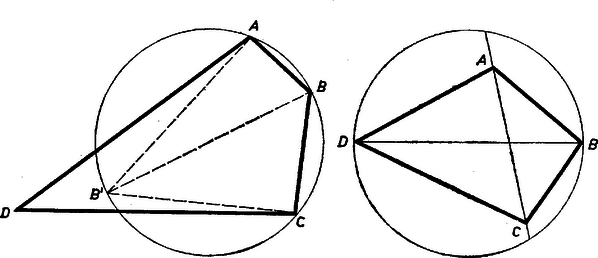
 
1. feladat. Bizonyitsuk be, hogy ha egy konvex négyszögnek 3 szöge tompaszög, akkor a negyedik szög csúcsából kiinduló átló hosszabb a másik átlónál.
 
I. megoldás. Legyen az ABCD konvex négyszög A, B és C csúcsánál levő szöge tompaszög. Írjunk kört az A, B, C csúcsok köré, ennek B-vel átellenes pontja legyen B'. Ez a BAD szögtartománynak is, a BCD szögtartománynak is a belsejében van, ugyanis Thalész tétele szerint BAB'∢=BCB'∢=90∘, az AB' és CB' félegyenes is a megfelelő szögtartomány belsejében halad. Ebből következik, hogy a BB'D konvex szög a BAD∢, BOD∢ egyikénél nagyobb, tehát tompaszög. Igy a BB'D háromszög legnagyobb oldala nagyobb BB'-nél, ez pedig, mint körátmérő, nem kisebb a kör AC húrjánál.
 
 

II. megoldás. Az előző megoldás jelöléseit és feltételeit használjuk. Rajzoljunk kört a BD átló mint átmérő fölé. Azok a pontok, amelyekből BD tompaszögben látszik, a kör belsejében vannak, így A és C is. AC tehát a kör belsejében levő szakasz, s így kisebb, mint a kör átmérője, BD.
 
Megjegyzés. Csak azt használtuk fel mind a két megoldásban, hogy A-nál és C-nél tompaszög van. Ebből a négyszög konvex volta is következik. Így azt bizonyítottuk be, hogy ha egy négyszög két szemben fekvő szöge tompaszög, akkor az ezek csúcsát összekötő átló rövidebb a másik átlónál.
 
A verseny 2. feladata ugyanaz volt, mint az általános versenyen; megoldását lásd ezen kötet 52-53. oldalain.
 
3. feladat. Fogadjuk el igaznak a következő állításokat:
a) Van olyan televízió-tulajdonos, aki nem szobafestő.
b) Akinek bérlete van a Gellért-fürdőbe, de nem szobafestő, az nem televízió-tulajdonos.
Döntsük el és indokoljuk meg, hogy következik-e a)-ból és b)-ből az alábbi állítás:
c) Nem minden televízió-tulajdonosnak van bérlete a Gellért-fürdőbe.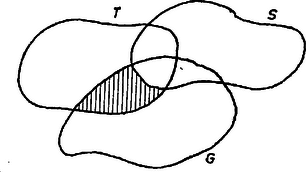
 
 

1. megoldás. Rajzoljunk a síkban egy T, egy S és egy G tartományt úgy, hogy legyen mindháromnak közös része, bármely kettő közös részének legyen olyan része, amelyik nem tartozik a harmadikhoz, és legyen mindegyiknek a másik kettőn kívül eső része ís. Gondoljuk a televízió-tulajdonosokat a T-tartomány belsejének pontjaival jelölve, a szobafestőket az S pontjaival, azokat pedig, akiknek bérletük van a Gellért-fürdőbe, a G pontjaival. Ekkor a b) állítás azt jelenti, hogy a G-be, de S-en kívül teendő pontok, ha vannak, nem kerülhetnek T-be sem, tehát az a tartomány, ami T-hez és G-hez is tartozik, de S-en kívül fekszik, egyetlen kijelölt pontot sem tartalmaz. Ezt az ábrán vonalkázással jelöltük.
Az a) állítás szerint van pont a T-nek B-hez nem tartozó részében. Ez nem kerülhet a bevonalkázott részbe, tehát G-n is kívül van, vagyis olyan televízió-tulajdonost jelöl, akinek nincs bérlete a Gellért-fürdőbe. Eszerint a c) állítás következik a)-ból és b)-ből.
 
II. megoldás. A b) állítás így is fogalmazható: nincs olyan televízió-tulajdonos, aki nem szobafestő, de bérlete van a Gellért-fürdőbe. Eszerint egy olyan televízió-tulajdonosnak, akire az a) állítás teljesül, nem lehet bérlete a Gellért-fürdőbe. Mivel az a) állítás ilyen személy létezését mondja ki, így a)-ból és b)-ből következik a c) állítás.
Surányi János