Cím: 1965. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1966/május, 194 - 198. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Mely egész a, b, c értékek elégítik ki az

a2+b2+c2+3<ab+3b+2c(*)
egyenlőtlenséget?
 

Megoldás. Minthogy egyenlőtlenségünk mindkét oldalán egész szám áll, az egyenlőtlenség akkor és csak akkor teljesül, ha a baloldal legalább 1-gyel kisebb a jobboldalnál, ha tehát
a2+b2+c2+4≤ab+3b+2c.
Ezt az egyenlőtlenséget
(a-b2)2+3(b2-1)2+(c-1)2≤0
alakba írva megállapíthatjuk, hogy csak akkor teljesülhet, ha benne minden négyzet alapja 0, hiszen különben a baloldalon pozitív szám állana. Eszerint
a-b2=0,b2-1=0,c-1=0,
és az egyetlen megoldás
a=1,b=2,c=1.

 

Második feladat. Egy körlemezen 8 pontot veszünk fel (a határoló körvonalat is a körlemezhez számítjuk). Bizonyítsuk be, hogy a 8 pont között van két olyan, amelynek távolsága a kör sugaránál kisebb.
 

I. megoldás. A 8 pont között legalább 7 a kör középpontjától különböző pont van. Minden ilyen pont a középponttal összekötve a kör egy-egy sugarát határozza meg. Ha ezek a sugarak nem mind különbözők, két pont ugyanannak a sugárnak a körközépponttól különböző pontja, s így távolságuk a sugárnál kisebb.
Ha viszont csupa különböző sugárhoz jutottunk, akkor ezek az O középpontnál elhelyezkedő teljes szöget legalább 7 szögre bontják fel, s ezért van közöttük két olyan sugár, amelynek szöge a teljes szög hatodrészénél, 60∘-nál kisebb. Legyen a 8 pont közül való A és B ezen a két sugáron (1. ábra).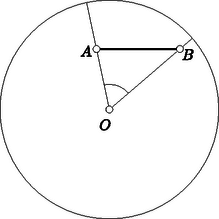
 
 

1. ábra
 

Minthogy AOB∢<60∘, van az OAB▵-nek nagyobb szöge is. A háromszög szögeiről és szemközti oldalairól szóló tételre hivatkozva kimondhatjuk ezért, hogy az OAB▵-nek van AB-nél nagyobb oldala, hogy tehát AB kisebb az OA, OB távolságok valamelyikénél, s így kisebb az utóbbiaknál nem kisebb körsugárnál is.
Minden esetben eljutottunk tehát a 8 pont közül két olyanhoz, amely kielégíti a feladat követelményét.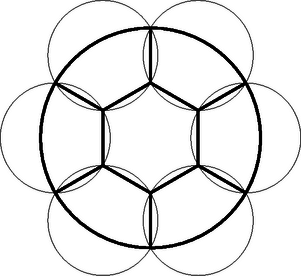
 
II. megoldás. A körlemezt egy beírt szabályos hatszög csúcsaihoz vezető 6 sugár és ezek felezőpontjai által meghatározott szabályos hatszög segítségével 7 tartományra bontjuk fel (2. ábra). E tartományok mindegyike egy-egy olyan körben helyezkedik el, amelynek átmérője az eredeti kör sugara. Ez az eredeti körrel koncentrikus és feleakkora sugarú körre, valamint a beírt szabályos hatszög oldalaihoz tartozó Thales-körökre valóban teljesül.
 

 

2. ábra
Tekintsük most a megadott 8 pontot, és forgassuk el a kört tartományokra felosztó vonalakat a kör középpontja körül úgy, hogy a 8 pont egyike se essék felosztó vonalra. Ekkor a 7 tartomány valamelyikében legalább két pontnak kell elhelyezkednie. E két pont az illető tartományt leborító kör belsejében van, s így távolságuk a kör átmérőjénél, azaz az eredeti kör sugaránál kisebb.
 
Megjegyzések. 1) Nyilvánvaló, hogy a feladatban nem írhatunk 8 helyébe 7-et, hiszen a kör középpontja és egy beírt szabályos hatszög csúcsai 7 olyan pont, amelyek között nem lép fel a kör sugaránál kisebb távolság. Első megoldásunkból azt is kiolvashatjuk, hogy más ilyen ellenpélda nincs.
2) Jelölje an a körbe írt szabályos n-szög oldalát. A feladat állítása szerint a körlemezen felvett 8 pont között van kettő, amelynek távolsága a6-nál kisebb. Bebizonyítjuk, hogy a két pont mindig megválasztható úgy is, hogy távolságuk ne legyen a7-nél nagyobb. A kör középpontja és egy beírt szabályos hétszög csúcsai mutatják, hogy a tétel állítása ilyen irányban tovább már nem finomítható.
A bizonyítás gondolatmenete második megoldásunkéhoz hasonló, de bizonyos szempontból azzal éppen ellentétes lesz. A kört most 8 tartományra bontjuk fel. Egy beírt szabályos hétszög leghosszabb átlói egy kisebb szabályos hétszöget burkolnak. Ennek csúcsai az eredeti hétszög csúcsaihoz vezető sugarakon helyezkednek el. A felbontást most a kisebb hétszög és a hétszögcsúcsokat összekötő sugárszakaszok szolgáltatják (3. ábra).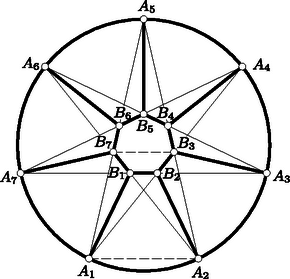
 
 

3. ábra
 

Azt állítjuk, hogy a 8 tartomány bármelyikén veszünk is fel két pontot (határpont felvételét is megengedve), ezek távolsága a7-nél nagyobb nem lehet. Ez a kis hétszög esetében nyilvánvaló, hiszen egy szabályos hétszög pontjai közül egy legnagyobb átló végpontjai vannak egymástól legtávolabbra, és a kis hétszög B7B3 átlója az ábra A1A2A5▵-éből kiolvashatóan kisebb, mint A1A2=a7.
A szektorszerű A1A2B2B1 tartományra térve először is belátjuk, hogy A1A2=A2B1 (s ugyanígy =A1B2). Ez abból adódik, hogy az A1A2B1A7 négyszög rombusz, mert szemközti oldalai párhuzamosak és A7A1=A1A2=a7, így tehát az A1B1 átló a rombuszból egyenlőszárú háromszöget vág le. Ennek szárszöge a kör egyharmadánál kisebb íven (ti. kéthetedén) nyugvó kerületi szög, ezért 60∘-nál kisebb, s így az egyenlőszárú háromszög A1B1 alapja az A1A2=a7 szárnál kisebb.
Ha a szektorszerű tartományban két egymástól maximális távolságra levő pontot keresünk, nyilván csak a határvonal pontjai jöhetnek szóba. A maximális szakasz végpontjai között nem szerepelhet egy határoló szakasz belső pontja, mert valamely pontnak egy szakasz pontjaitól mért távolságai közül a maximális értéket csak végponttól mért távolság adhatja. Nem szerepelhet a maximális szakasz végpontjai között az A1A2 körív belső pontja sem, mert a körlemez valamely (a középponttól különböző) pontjának egy körív pontjaitól mért távolságai közül a maximális értéket szintén csak végponttól mért távolság adhatja. Így tehát a keresett maximális szakasz mindkét végpontja csak az A1, A2, B2, B1 pontok közül való lehet, s e pontok távolságainak maximuma, mint láttuk, valóban a7.
Tekintsük most már a körlemez megadott 8 pontját. Ha mindannyian a kis hétszögben vannak, akkor bármelyik kettőnek a távolsága kisebb, mint a7. Ha nem ez a helyzet, forgassuk el a tartományainkat határoló vonalakat a kör középpontja körül úgy, hogy a 8 pont valamelyike elválasztó vonalra essék. Ekkor a tartományok mindegyike tartalmaz a belsejében és a határán valahány pontot (esetleg egyet sem) a 8 pont közül. E számok összege legalább 9, hiszen van olyan pont, amelyet kétszer is figyelembe vettünk. Kell tehát a 8 tartomány között olyannak lennie, amely a határát is hozzászámítva legalább két pontot tartalmaz pontjaink közül. E kettőnek a távolsága azonban a fentiek szerint legfeljebb a7, s ez állításunk helyességét bizonyítja.
 

Harmadik feladat. Olyan felfelé keskenyedő, négyzetalapú szabályos csonkagúlát tekintünk, amelynek az alaplapja köré írt kör sugara kisebb, mint az oldallapjai köré írt körök sugara. Bizonyítsuk be, hogy egy testátló két végpontját összekötő, a csonkagúla felületén haladó legrövidebb vonal a csonkagúla palástján helyezkedik el.
 

Megoldás. Tekintsük az ABCD alapú, EFGH fedőlapú szabályos csonkagúlát (4. ábra). A forgásszimmetria miatt mindegy, hogy melyik testátló végpontjait összekötő vonalakkal foglalkozunk. Ha az AG testátlót választjuk, megállapíthatjuk, hogy minden összekötő vonalnak metszenie kell a térbeli BCDHEF hatszöget. Minthogy pedig e hatszög minden pontját A-val és G-vel a csonkagúla felületén elhelyezkedő szakasz köti össze, és két pont összekötő szakasza minden más összekötő vonalnál rövidebb, a legrövidebb összekötő vonal csak két szakaszból álló töröttvonal lehet.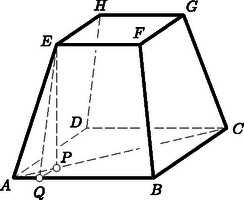
 
 

4. ábra
 

Ez vagy egy oldallapon és a fedőlapon, vagy az alaplapon és egy oldallapon, vagy pedig két oldallapon helyezkedik el. A szimmetria miatt mindegy, hogy itt melyik oldallap vagy melyik két szomszédos oldallap szerepel.
A vizsgált töröttvonal mindhárom esetben két olyan lapon halad, amelyek élben csatlakoznak. Ha e lapokat az él körül egy síkba forgatjuk, a töröttvonal is a síkba terül, s akkor lesz a legrövidebb, ha a kiterítés után nincs már törése, azaz a végpontokat összekötő egyetlen szakasszá válik. Ez persze csak akkor lehetséges, ha a kiterítés után adódó végpontok összekötő szakasza metszi a két lap közös élét. Megmutatjuk, hogy ez a bennünket érdeklő esetek mindegyikében bekövetkezik.
Csonkagúlánk ABFE oldallapja szimmetrikus trapéz, melynek AB alapvonalán 45∘-nál nagyobb (és EF fedővonalán 135∘-nál kisebb) szögek nyugszanak. Ha ugyanis P és Q az E csúcsnak az alapsíkra, illetőleg az AB élre vetett vetülete, akkor az APQ▵ egyenlőszárú derékszögű, tehát EQ>PQ=AQ miatt az AEQ▵-ben a nagyobbik befogóval szemközti EAQ∢>45∘.
A feladat követelményére támaszkodva most azt igazoljuk, hogy α=AFB∢<45∘. Az alaplap köré írt körben az AB húron 45∘-os (és 135∘-os) kerületi szögek nyugszanak. Minthogy az oldallap köré írt kör sugara nagyobb, ebben az AB húron nyugvó kerületi szögek 45∘-nál kisebbek és 135∘-nál nagyobbak. Mivel pedig az AFB∢ része a 135∘-nál kisebb EFB∢-nek, valóban csak 45∘-nál kisebb lehet.
Tekintsük most már az említett három esetnek megfelelő, kiterítéssel keletkező ábrákat (5. ábra). A testátló végpontjaiból a kiterítés után adódó pontokat összekötő (vastagon meghúzott) szakasz mind a három esetben metszi a két lap közös élét. Mindhárom esetben szerepel ugyanis olyan konvex négyszög, amelynek egyik átlója a közös él, másik átlója pedig a szóban forgó összekötő szakasz. E négyszögek két szemközti oldalát szaggatottan húztuk meg. Konvexitásuk csak az a) és c) ábrarészben kíván alátámasztást, s az a) ábrában AEF∢<135∘, valamint FEG'∢=45∘, a c) ábrában pedig AFB∢<45∘, valamint BFG''∢<135∘ következménye.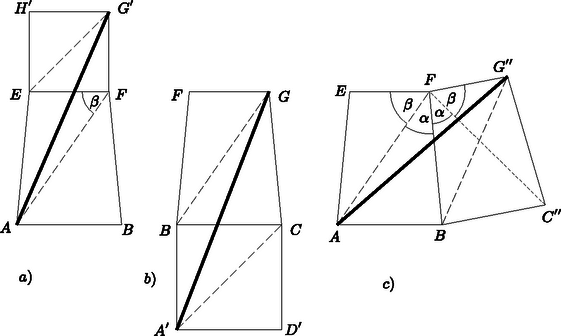
 
 

5. ábra
 

Már csak annak megmutatására van szükségünk, hogy a vastagon meghúzott szakasz a c) ábrában a legrövidebb. A b) ábra szakasza nyilván hosszabb az a) ábráénál, hiszen vízszintes (a közös él egyenesére vetett) vetülete ugyanakkora, függőleges vetülete pedig nagyobb, mert az alapél nagyobb, mint a fedőél. Azt kell csak bizonyítanunk, hogy az a) és c) ábra szakaszaira AG'>AG''. Ezek a szakaszok az AFG'▵ és AFG''▵ oldalai, amelyekben két-két oldal páronként egyenlő. Ezért az ismert tételre hivatkozva
AFG'∢>AFG''∢
igazolása szükséges, ez azonban β=AFE∢ jelöléssel
90∘+β>2α+β
alakban írható, s a már bizonyított α<45∘ következménye.
 
 Hajós György