Cím: Az 1965. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, haladók versenye, a speciális matematikai osztályok feladatai
Szerző(k):  Lőrincz Pál ,  Surányi János 
Füzet: 1966/március, 97 - 101. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1965. évi Arany Dániel tanulóversenyek II. fordulóján
kitűzött feladatok megoldása

 
Haladók (legfeljebb II. osztályosok) versenye
(2. közlemény)

 
A speciális matematikai osztályok feladatai
 
1. feladat. Bizonyítandó, hogy ha n kettőnél nagyobb és egész, akkor
(2n-1)n+(2n)n<(2n+1)n.(1)

Megoldás. Az egyenlőtlenséget az átrendezett
(2n)n<(2n+1)n-(2n-1)n(1a)
alakban fogjuk bizonyítani. Rendezzük a jobb oldali hatványokat 2n hatványai szerint. Mind a két kifejezés (a+b)n alakú, ahol a=2n, és b az egyik esetben 1, a másik esetben -1. Az n-edik hatvány egy n tényezős szorzatot jelent. Ennek a tagokra bontott alakját úgy kapjuk, hogy minden lehető módon kiveszünk mindegyik tényezőből egy-egy tagot, ezeket összeszorozzuk, és az összes ilyen szorzatokat összeadjuk.
Végezzük a fenti két hatvány tagokra bontását párhuzamosan úgy, hogy mindkettőben ugyanannyiadik tényezőkből választjuk a 2n-et és a többiből az első kéttagúnál a +1-et, a másodiknál a -1-et. Ha páros számú tényezőből választjuk a +1-et, ill. a -1-et, akkor egyenlő tagok keletkeznek, és ezek a kivonáskor kiesnek (így az a két tag is, amelyhez mindegyik tényezőből a 2n-et választjuk ki). Ha viszont páratlan számú tényezőből választjuk a +1-et, illetőleg a -1-et, akkor egyenlő abszolút értékű tagok keletkeznek, de (2n+1)n-ből pozitív előjellel, (2n-1)n-ből negatív előjellel, a kivonásnál tehát ezek kétszerese adódik. Az összes ilyen tagok összege adja a jobb oldalt. Azt csökkentjük tehát, ha ezek közül a tagok közül csak egyeseket veszünk tekintetbe.
Nézzük azokat a tagokat, amelyek úgy keletkeznek, hogy egy híjján minden tényezőből a 2n-et választjuk. Egyrészt ezek mindegyike 2(2n)n-1-t ad a különbséghez, másrészt ilyen tag n-szer keletkezik, mert az a tényező, amelyikből nem a 2n-et (tehát az 1-et, ill. a -1-et) választottuk, vagy az első vagy a második stb. vagy az n-edik. Az (1a) jobb oldala tehát legalább n⋅2⋅(2n)n-1=(2n)n, és nagyobb ennél, ha fennáll az a lehetőség is, hogy három tényezőből válasszuk a +1-et, ill. a -1-et, vagyis ha n legalább 3. Ezzel az egyenlőtlenséget bebizonyítottuk.
 
Megjegyzés. A követett gondolatmenet mutatja, hogy (a+b)n-t a és b hatványai szerint rendezve akbn-k alakú tagok keletkeznek, ahol k=0,1,2,...,n lehet, és a felírt tag együtthatója az a szám, ahányféleképpen n különböző dolog közül k-t ki lehet választani, ha a kiválasztás sorrendjére nem vagyunk tekintettel. (Ennyi módon választhatunk ki k tényezőt, hogy azokból a-t, a többiből b-t vegyük ki tényezőül.)
 
II. megoldás. Kézenfekvő (1a) jobb oldalának első tagjából levonni, a másodikhoz hozzáadni (2n)n-t, mivel a kifejezést 2n egy hatványával akarjuk összehasonlítani. Ekkor a fellépő különbségekben az alapok különbsége 1, és ezért az egyenlő kitevőjű hatványok különbsége így alakítható át:
(2n+1)n-(2n-1)n=(2n+1)n-(2n)n+(2n)n-(2n-1)n==(2n+1)n-1+(2n+1)n-2⋅(2n)+(2n+1)n-3(2n)2+...+(2n+1)(2n)n-2++(2n)n-1+(2n)n-1+(2n)n-2⋅(2n-1)+...+(2n)(2n-1)n-2++(2n-1)n-1=[(2n+1)n-1+(2n-1)n-1]+(2n)[(2n+1)n-2++(2n-1)n-2]+...+(2n)n-2[(2n+1)+(2n-1)]+2(2n)n-1.

A kifejezést n tagra bontottuk, így az egyenlőtlenség igazolást nyer, ha megmutatjuk, hogy a kifejezés növekszik, ha mindenütt, ahol előfordul, 2n+1-et és 2n-1-et egyidejűleg (2n)-nel helyettesítjük. Az utolsó előtti tagnál ez nem okoz változást, a többinél viszont nagyobbítást jelent, ugyanis ha l>1,
(2n+1)l+(2n-1)l-2(2n)l=(2n+1)l-(2n)l-[(2n)l-(2n-1)l]==(2n+1)l-1+(2n+1)l-2⋅(2n)+...+(2n+1)(2n)l-2+(2n)l-1--[(2n)l-1+(2n)l-2⋅(2n-1)+...(2n)(2n-1)l-2+(2n-1)l-1]==[(2n+1)l-1-(2n-1)l-1]+(2n)[(2n+1)l-2-(2n-1)l-2]+...++(2n)l-2⋅[(2n+1)-(2n-1)]>0.

Ezzel a feladat állítása igazolást nyert.
 

Megjegyzés. Az egyenlőtlenség belátható az egyenlő kitevőjű hatványok különbségére vonatkozó azonosság ismételt alkalmazásával is:
(2n+1)n-(2n-1)n=(2n+1)n-(2n)n+(2n)n-(2n-1)n==[(2n+1)n-1+(2n-1)n-1]+(2n)[(2n+1)n-2+(2n-1)n-2]++...+(2n)n-2⋅[(2n+1)+(2n-1)]+2(2n)n-1.



Itt az utolsó előtti tag egyenlő az utolsóval, a többi pedig nagyobb nála, mert ha l>1,
(2n+1)l+(2n-1)l-2(2n)l=(2n+1)l-(2n)l-[(2n)l-(2n-1)l]==(2n+1)l-1-(2n-1)l-1+(2n)[(2n+1)l-2-(2n-1)l-2+...++(2n)l-2⋅[(2n+1)-(2n-1)]>0.


Az n tag összege tehát nagyobb, mint n⋅2(2n)n-1=(2n)n.
 
2. feladat. Legyen adva egy egyenlő szárú trapéz. Tekintsük azt a két háromszöget, melyek közös oldala a trapéz egyik szára, harmadik csúcsaik a másik szár végpontjai. ‐ Bizonyítsuk be, hogy a két háromszög beirt körének középpontját összekötő egyenes merőleges a trapéz párhuzamos oldalaira.
 
I. megoldás. Legyen az adott egyenlő szárú trapéz ABCD, ahol a csúcsokat úgy betűztük, hogy AB‖CD és AB≥CD álljon. Jelöljük az ABC háromszögbe írt kör középpontját O-val, a BCD háromszögbe írtét Q-val, az előbbi kör érintési pontját AB-n S-sel, az utóbbiét CD-n Z-vel. A feladat állítása igazolást nyer azzal, ha megmutatjuk, hogy SZ merőleges a párhuzamos oldalakra, hiszen O az AB-re S-ben emelt merőlegesen van, Q pedig a CD-re Z-ben állított merőlegesen. D vetületét AB-n T-vel jelölve azt mutatjuk meg, hogy DTSZ téglalap. Ehhez elég megmutatni, hogy DZ=TS, hiszen ez a két oldal párhuzamos és merőleges DT-re.
 
 

A háromszög csúcsainak a beírt kör érintési pontjától való távolsága és az oldalak hossza közti ismert összefüggés szerint
AS=12(AB+AC-BC),DZ=12(DC+DB-BC).
A T pont az AB szakaszon van (esetleg egybeesik A-val), így a TS szakasz, figyelembe véve, hogy az átlók egyenlők,

TS=AS-AT==12(AB+DB-BC)-12(AB-CD)==12(DB+CD-BC)=DZ,



DTSZ tehát valóban téglalap. (Nem lehet, hogy O és Q egybeessék, s így a rajtuk átmenő egyenes iránya határozatlan, mert akkor a körök is egybeesnének, hiszen mindkettő érinti BC-t; de pl. az ABC háromszögbe írt kör nem érintheti CD-t, mert CD-nek C az egyetlen közös pontja a háromszöggel, az pedig a körön kívül van.
 
Megjegyzés. Hasonlóan lehet belátni, hogy a BCA és BOD háromszög külső érintő köreinek középpontjai ‐ alkalmas páronként összekötve ‐ ugyancsak az AB-re merőleges egyeneseket adnak.
 

II. megoldás. Az előző megoldás jelöléseit használjuk. A trapéz köré kör írható. Legyen a kör A-t (és D-t) nem tartalmazó BC ívének felezőpontja F. Megmutatjuk, hogy az OFQ háromszög egyenlő szárú és OQ-ra merőleges szimmetriatengelye párhuzamos a trapéz párhuzamos oldalaival. Ezzel a feladat állítása bizonyítást nyer.
Az állítás első része abból következik, hogy OFB és QFB egyenlő szárú háromszögek. AO és BO szögfelezők, és előbbi átmegy F-en. Így, felhasználva a külső szög és a kerületi szög tételét:
FOB∢=FAB∢+OBA∢=FAC∢+OBC∢==FBC∢+CBO∢=FBO∢.


Hasonlóan látható a QFB háromszög egyenlő szárú volta is. A kettőből OF=BF=QF, tehát OFQ is egyenlő szárú háromszög. Szimmetriatengelye az OFQ∢=AFD∢ felezője, átmegy a B-t nem tartalmazó AD ív G felezőpontján. Ez az F pont tükörképe a trapéz szimmetriatengelyére, így FG valóban párhuzamos a párhuzamos oldalakkal, OQ tehát merőleges rájuk.
 

3. feladat. Adott egy kör és a kör belsejében fekvő P pont. Legyen a körvonal tetszőleges pontja Q és a Q pontbeli érintője e. Jelöljük a kör középpontjából a PQ-ra emelt merőleges és e egyenes metszéspontját M-mel. ‐ Mi az M pontok mértani helye, ha Q végigfut a kör kerületén?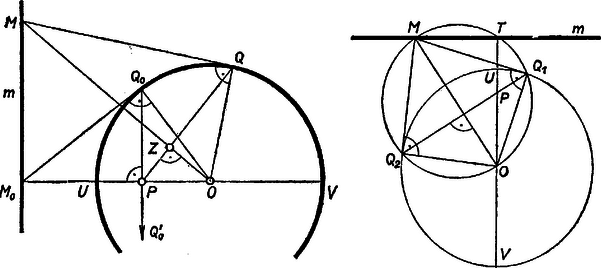
 
 

I. megoldás. Csak a kör O középpontjától különböző P pontok esetével kell foglalkoznunk, mert ha P egybeesik O-val, akkor Q semmilyen helyzetében nem jön létre az M metszéspont. Nem jön létre az M pont akkor sem, ha P különbözik O-tól, de Q a körből OP-vel kimetszett UV átmérő bármelyik végpontjában van.
Megszerkesztve M-et Q néhány helyzetéhez, a kapott pontok egy egyenesbe esnek, amely merőleges OP-re. Megmutatjuk, hogy a mértani hely valóban egyenes.
A mértani helynek van pontja az OP egyenesen. Akkor kapjuk ezt, amikor az O-n át PQ-ra állított merőleges maga OP, vagyis amikor PQ merőleges OP-re, más szóval Q a kör P-n átmenő, OP-re merőleges Q0Q'0 húrjának valamelyik végpontjában van. Legyen a Q0-hoz és Q'0-höz tartozó pont M0. Ekkor az OQ0M0 és OPQ0 derékszögű háromszögek hasonlók, mert O-nál levő szögük közös, így
M0O:Q0O=Q0O:PO,M0O⋅PO=Q0O2.
(2)
M0 az OP félegyenesen van.
Legyen a körnek egy az U, V, Q0, Q'0 pontoktól különböző pontja Q, és messe OM a PQ egyenest Z-ben. Az OQM és OZQ háromszögekből az előbbiekhez hasonlóan, majd felhasználva (2)-t
MO⋅ZO=QO2=Q0O2=M0O⋅PO,tehátMO:M0O=PO:ZO.


A két egyenlő arány tagjai az MM0O és PZO háromszögek O-ból kiinduló oldalai. E háromszögek O-nál levő szöge közös, így hasonlók, ezért MM0O∢=PZO∢=90∘. Ezzel beláttuk, hogy M valóban mindig az M0-ban OM0-ra, vagyis OP-re merőlegesen álló m egyenesen van.
m minden pontja hozzátartozik a mértani helyhez. Láttuk ugyanis, hogy M0 a kört befutó pont Q0 és Q'0 helyzeteihez tartozik hozzá. Legyen m-nek egy az M0-tól különböző pontja M*, és az M*-ból a körhöz húzott egyik érintő érintési pontja Q*. Ez csak M*-ot szolgáltathatja, mert U-tól és V-től különbözik, m-en levő pontot szolgáltat, de a Q*-ban húzott érintő egyetlen közös pontja m-mel M*, tehát M* valóban hozzátartozik a mértani helyhez.
Mindezek szerint a keresett mértani hely az OP félegyenesre a (2)-nek eleget tevő M0 pontjában állított merőleges.
 

II. megoldás. P-n át tetszés szerinti, de O-n át nem menő egyenest húzva, ennek a körrel való Q1, Q2 metszéspontjaihoz közös M pont tartozik. Ugyanis M-mel a Q1-beli és Q2-beli érintők metszéspontját jelölve az MQ1OQ2 négyszög deltoid, mert O-ból kiinduló oldalai, valamint a végpontjaiknál levő szögek egyenlők, tehát MO átlója merőleges a Q1Q2 átlóra. Ez pedig azonos a PQ1, PQ2 egyenessel, tehát az előírás szerint Q1-hez és Q2-höz M tartozik hozzá.
A deltoid köré kör írható, mert a szemben fekvő Q1, Q2 csúcsainál levő szögek összege két derékszöggel egyenlő, így MO e körben átmérő. Messe ez a kör az OP egyenest másodszor T-ben, így Thalész tétele szerint az OTM szög derékszög.
Könnyű belátni, hogy T helyzete független a Q1Q2 egyenes megválasztásától. A deltoid köré írt körnek TO és Q1Q2 a P-n átmenő húrjai, így
PT⋅PO=PQ1⋅PQ2.
Hasonlóan az adott körből
PQ1⋅PQ2=PU⋅PV,
ahol U, V ismét az adott körnek PO-n levő pontjai, így
PT⋅PO=PU⋅PV.
Itt PO, PU és PV állandó, tehát PT is állandó, amint állítottuk.
Ezek szerint M mindig az OP egyenesre az állandó T pontban állított m merőlegesen van.
Eredményünk alapján m az M egyetlen helyzetéből megszerkeszthető. Ha pl. a P-n át választott egyenes merőleges OP-re, akkor M az OP-n, tehát éppen T-ben adódik.
Az I. megoldáshoz hasonlóan látható be, hogy m minden pontja a mozgó pont egy helyzetéhez tartozik, m a keresett mértani hely.
 Lőrincz Pál, Surányi János