Cím: Megjegyzés egy 1965. évi versenyfeladathoz
Szerző(k):  Lovász László 
Füzet: 1966/május, 201 - 203. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1965. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulójának 2. feladata így szólt:
A hegyesszögű háromszögbe négyzetet írunk, amelynek két csúcsa az egyik oldalon, egy-egy csúcsa a további oldalakon van. Bizonyítsuk be, hogy a négyzet tartalmazza a háromszög beírt körének középpontját.
A közölt megoldások* szerint a négyzet e pontot mindig belsejében tartalmazza, továbbá elég a négyzet és a háromszög közös oldalegyenesén fekvő csúcsokról kikötni, hogy hegyesszögűek legyenek.
Pelikán József versenydolgozatában felvetette azt a kérdést, hogy rögzítve a négyzetet és minden lehetséges módon köréírva hegyesszögű háromszögeket, ezek beírt köreinek középpontjai kerülhetnek-e a négyzet oldalaihoz tetszés szerint közel, vagy van olyan λ>0, hogy ha a négyzet oldala t, akkor a körülírt háromszögek beírt köreinek középpontjai mindig legalább λt távolságra esnek a négyzet oldalaitól. Az alábbiakban meghatározzuk azon pontok mértani helyét a négyzetben, amelyek beírt körközéppontok lehetnek, és látni fogjuk, hogy ezek nem kerülhetnek tetszés szerint közel az oldalakhoz.
Legyen DEFG a négyzet, ABC egy körülírt háromszöge, legyenek a B, D, E, C pontok ebben a sorrendben egy egyenesen, s legyen F, ill. G az AC, ill. AB szakaszon. Legyen az ABC háromszög beírt köre k, középpontja O.
I. Egyelőre nem kötjük ki, hogy a BAC szög hegyesszög legyen.

 
 

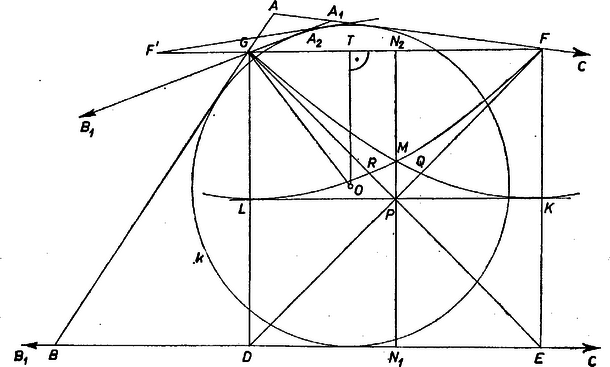
a) A k körnek metszenie kell az FG szakaszt; különben ugyanis átmérője legfeljebb DE lenne, ezért az EF, GD szakaszok közül legalább az egyiket, mondjuk EF-et nem metszené, s így teljes egészében az EFG szögtartományban volna, s így nem érinthetné az AC egyenest. Legyen EF és GD felezőpontja K, ill. L, akkor ezek szerint O a KLGF téglalapba esik.
k nem tartalmazhatja belsejében a G pontot, mert G-ből érintő vonható hozzá. Így O legalább annyira van G-től, mint a DE egyenestől, tehát alatta van a G fókuszú, DE vezéregyenesű parabolának. Hasonlóan O az F fókuszú, DE vezéregyenesű parabolának is alatta van, legyen e két parabola metszéspontja M. Ekkor O az (egy egyenes szakasz és két parabolaív által határolt) KLM idomba esik; a KL szakasz pontjai nem tartoznak hozzá e mértani helyhez.
b) Ennek a tartománynak minden pontja lehet körközéppont. Valóban, legyen O ezen idom valamely pontja. Az O körül írt, DE-t érintő k kör nem tartalmazza F-et és G-t és metszi FG-t, így az F-ből, ill. G-ből k-hoz húzott, a négyzetet nem metsző érintők és DE egy olyan háromszöget határolnak, melynek a DE egyenesen levő csúcsaiban hegyesszögei vannak és melynek a k kör beírt köre, DEFG beírt négyzete.
II. Kössük ki most még, hogy A-nál is hegyesszög van.
a) Az I.a) alatti megállapítások természetesen érvényben maradnak. Jelöljük DEFG átlóinak metszéspontját P-vel. Megmutatjuk, hogy ekkor O csak a PFG háromszög belsejében lehet! Ebből következik, hogy ha az F fókuszú parabolának és a DF átlónak a négyzetbe eső metszéspontját Q-val, a G fókuszú paraboláét és EG-ét R-rel jelöljük, O a (két egyenesszakasz és két parabolaív által határolt) PQMR idomba esik; a PQ, PR szakaszok pontjai nem tartoznak a mértani helyhez. Annak bizonyítását, hogy ezen idom minden pontja hozzátartozik a mértani helyhez, az olvasóra bízzuk.
Tegyük fel az állítással ellentétben, hogy k középpontja pl. a PDG háromszögbe esik. Ekkor k nem metszi az EF egyenest, és ezért a CA oldalt az FA szakaszon érinti. A G pontból két érintőt húzhatunk k-hoz; az ezek által lemetszett háromszögek legyenek ABC és A1B1C. Feltehetjük, hogy a jelölést úgy választottuk, hogy k az A1G, GB szakaszokat érinti. Be fogjuk látni, hogy a B1A1C és BAC szögek tompaszögek. A B1A1C szög a GAA1 háromszög külső szöge, s így nagyobb a BAC szögnél.
Nyilvánvalóan BGO∢=A1GO∢. Továbbá DGO∢≤OGF∢, ezért BGD∢≥FGA1∢. Legyen O vetülete FG-re T, és F tükörképe T-re F', ez O elhelyezkedése miatt a négyzet oldalának meghosszabbításán fekszik. Messe az FA érintő OT-re vett tükörképe GA1-et A2-ben, akkor az FGA1 szög a GF'A2 háromszög külső szöge, és így GF'A2∢<FGA1∢. Továbbá nyilvánvalóan GF'A2∢=GFA∢. Ezek szerint
GFA∢<FGA1∢≤BGD∢,és

GAF∢=180∘-AGF∢-GFA∢=90∘+BGD∢-GFA∢>90∘
és még inkább GA1F∢>90∘.
Ezzel ellentmondásra jutottunk azzal a feltevésünkkel, hogy az ABC háromszög hegyesszögű. Tehát O a PGF háromszög belsejébe esik, és így a mértani hely valóban a PQMR idom belseje, hozzávéve a QM, MR parabolaíveket.
Ennek az idomnak a négyzet kerületéhez legközelebb eső pontja M, hiszen a négyzetet P-ből, mint középpontból úgy kicsinyítve, hogy M a kerületére essék, nyilván tartalmazni fogja a PQMR idomot. Legyen DE és FG felezőpontja N1, ill. N2, a négyzet oldala t, akkor M nyilván az N1N2 egyenesre esik,
MN1=t-MN2,ésMN1=MF=MN22+t24,
azaz MN2=3t/8. Tehát Pelikán kérdésére a válasz az, hogy a beírt körök középpontjai nem kerülhetnek 3t/8-nál közelebb a négyzet kerületéhez, és ez a korlát nem javítható.
Egyébként az is látható, hogy A-nál tompaszöget is megengedve a beírt kör középpontja tetszés szerinti közel eshet a négyzet kerületéhez.
 
 Lovász László
*Lásd Surányi János: Az 1965. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulóján kitűzött feladatok megoldása, K.M.L. 31 (1965) 104‐112. o., szorosabban 106‐110. o.