Kezdőlap


Cím:	A tehetetlenségi nyomaték és mérése
Szerző(k):	Keglevich László
Füzet:	1965/december, 225 - 234. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A tehetetlenségi nyomaték fogalma és összefüggései

Forgómozgásnál a test forgásában fellépő gyorsulást a

β

szöggyorsulással, azaz az egységnyi idő alatti szögsebesség-változással mérjük. A tapasztalat szerint a szöggyorsulás arányos a testre ható

F

forgatónyomatékkal:

\begin{matrix} F = I \cdot β \end{matrix}

(1)

I

arányossági tényező a test tengely körüli gyorsításával szemben tanúsított ellenállására, tehetetlenségére jellemző mennyiség. Szerepe épp olyan, mint haladó mozgásnál a tömegé. Ezért a test tengelyre vonatkozó tehetetlenségi nyomatékának nevezzük. Az elnevezés kifejezésre juttatja azt, hogy az

I

mennyiség a test forgásszerű tehetetlenségének a mértéke. Egysége az

1 {kgm}^{2}

, ill.

1 {gcm}^{2}

1. ábra

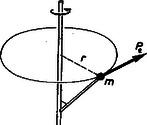Az (1) összefüggés nemcsak a tapasztalat alapján, hanem elméleti úton is megállapítható. Nézzük ezt meg egyetlen tömegpont esetére. Valamely súlytalan, merev karral

r

távolságra a tengelyhez rögzített kicsiny

m

tömegpontra hasson a tengely és a pont síkjára merőlegesen

P_{t}

erő (1. ábra). Ekkor a tömegpont pillanatnyi haladó mozgását tekintve érvényes Newton II. törvénye:

\begin{matrix} P_{t} = m \cdot a_{t} \end{matrix}

(2)

ahol a tömegpont érintő irányú gyorsulását

a_{t}

-vel jelöljük. Ez a valódi gyorsulásvektor érintő irányú (ún. tangenciális) ‐ komponense. A

P_{t}

erőn kívül szüntelenül hat még a merev kar révén egy erre merőleges, a középpont felé mutató, állandó nagyságú erő

P_{c}

is. Az utóbbi az

a_{t}

-re merőleges, középpont felé mutató, állandó értékű

a_{r}

radiális gyorsulás-komponenst eredményezi, amely az érintő irányú komponens nagyságát nem befolyásolja, csupán az irányát, biztosítva ezzel a körpályán való mozgást. Ha tehát a vizsgálat során feltételezzük, hogy a tömegpont körpályán mozog, akkor ezzel egyszer s mindenkorra figyelembe vettük a

P_{r}

hatását. A továbbiakban elegendő tehát csupán a

P_{t}

komponenssel foglalkozni.

2. ábra

Helyettesítsük most a

P_{t}

és

a_{t}

értékeket a forgómozgást jobban jellemző és ekkor ,,testhezállóbb''

F

és

β

mennyiségekkel az ismert

\begin{matrix} F = P_{t} \cdot r és a_{t} = β \cdot r \end{matrix}

(3)

összefüggések alapján. Ekkor

F

-et kifejezve azt kapjuk, hogy

\begin{matrix} F = m r^{2} \cdot β . \end{matrix}

(4)

Minthogy

m r^{2}

csak a mozgó tömeg nagyságára és a tengely helyzetére jellemző mennyiség, melynek nagysága a mozgás során nem változik, célszerű bevezetni az

\begin{matrix} I = m r^{2} \end{matrix}

(5)

mennyiséget, amelyet (4)-be helyettesítve gondolatmenetünk eredményéül máris megkaptuk az

\begin{matrix} F = I \cdot β \end{matrix}

előbbiekben tapasztalati úton megadott összefüggést. Ezt Newton II. törvényéhez való teljes formai és tartalmi hasonlósága miatt a forgómozgás dinamikai alaptörvényének nevezzük.
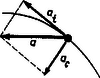
Itt még egyszer emlékeztetünk arra, hogy bár a tömegpontra ható erőnek csak egy részével, a

P_{c}

-vel számoltunk, a forgásszerű mennyiségekre átírt mozgástörvény mégis teljes és hű képet ad a mozgásról, sőt így könnyen és áttekinthetően is kezelhető. A teljes erőhatás többi részét, a

P_{t}

-t ugyanis a ,,forgó mozgás'' szóval állandóan figyelembe vesszük. Még egyszerűbb ezt elmondani a matematika nyelvén. Az erőt célszerűen felbontottuk tangenciális és radiális komponensekre, amelyekre külön-külön is érvényes Newton II. törvénye. Az (1) összefüggés egyszerűen az egyik, a tangencionális komponensre vonatkozó egyenlet, míg a másik erő állandó értékű és így az egyenletes körmozgást eredményezi. A felbontás természetesen éppen ezen az észrevételen alapul. (A dolog kicsit hasonlít a ferde hajlítás esetére, amelynél a könnyebb kezelhetőség kedvéért a mozgást szintén felbontjuk az egyszerűbb függőleges szabadesésre és vízszintes egyenletes mozgásra. Sőt, általában is megfigyelhető az, hogy bonyolultabb fizikai problémáknál a megfelelő ,,testhezálló'' részekre bontással, ill. a koordinátarendszer választással jutottak egyszerűen eredményhez.)
Jelen vizsgálataink szempontjából mindenekelőtt a levezetés során megállapított (5) összefüggés jelentős, mert ennek alapján felvilágosítást kapunk arra, hogy hogyan függ az

I

tehetetlenségi nyomaték értéke a forgó rendszer tulajdonságaitól. Mielőtt ezt közelebbről megvizsgálnánk, határozzuk meg, hogy kiterjedt testek esetén mi ennek a megfelelője.
Kiterjedt, több tömegpontból álló merev test, ill. rendszer esetén az (1) összefüggés pontonként érvényes:

\begin{matrix} F_{1} = I_{1} \cdot β, \\ F_{2} = I_{2} \cdot β, \\ . . ..., \\ F_{n} = I_{n} \cdot β . & (6) \end{matrix}

A megfelelő oldalak összeadásával a bal oldalon az eredő forgatónyomatékot kapjuk:

\begin{matrix} F = F_{1} + F_{2} + ... + F_{n}, \end{matrix}

(7)

a jobb oldalon viszont egy olyan összeget, melynek minden tagjából

β

kiemelhető, ez ugyanis ‐ merev testről lévén szó ‐ minden pontra azonos érték. Tehát

\begin{matrix} I_{1} β + I_{2} β + ... + I_{n} β = (I_{1} + I_{2} + ... + I_{n}) \cdot β . \end{matrix}

(8)

Ha a jobb oldalon ezután az

\begin{matrix} I = I_{1} + I_{2} + ... I_{n}, azaz I = \sum_{t = 1}^{n} m_{i} r_{i}^{2} \end{matrix}

(9)

helyettesítést alkalmazzuk, akkor ez esetben is a tapasztalattal megegyezően a tömegpontra érvényes

\begin{matrix} F = I \cdot β \end{matrix}

(1) összefüggést kapjuk. Látható tehát, hogy az (1) összefüggés a mozgó testekre általánosan érvényes, csupán az

I

tehetetlenségi nyomaték fogalmát kell (9) szerint általánosítani. Ez egyszerűen azt jelenti, hogy a test egyes pontjainak, ill. részeinek azonos tengelyre vonatkozó tehetetlenségi nyomatékai összegezhetők.
Az a megállapítás, hogy a forgó mozgásnál a test tehetetlenségi nyomatéka hasonló szerepet játszik, mint a haladó mozgásnál a tömeg, jól látható a forgó mozgásra érvényes

\begin{matrix} E_{k} = \frac{1}{2} I ω^{2} \end{matrix}

(10)

összefüggésből is, amely az előbbi gondolatmenethez hasonlóan nyerhető. Az összefüggésben

E_{k}

a mozgási energiát és

ω

a szögsebességet jelenti. A megfelelés teljes, mivel a sebesség és szögsebesség között is fennáll. A (10) összefüggés alapján ‐ (9) figyelembevételével ‐ érthető pl., hogy miért lehet a lendítőkerék energiáját növelni azonos szögsebesség és tömeg esetén azáltal, hogy a tömegeket a tengelytől messzebb teszik.
Az

I

tehetetlenségi nyomaték említett tulajdonsága ‐ hogy ez a forgó mozgásnál a haladó mozgás tömegének felel meg ‐ kitűnik még a torziós lengésből, ill. az itt érvényes

\begin{matrix} T = 2 π \sqrt[]{\frac{1}{D^{*}}} \end{matrix}

(11)

lengésidő képletből is. Ebben

T

a lengésidőt,

D^{*}

a direkciós forgatónyomatékot ‐ az egységnyi szögelforduláshoz tartozó forgatónyomatékot ‐ jelenti. (A torziós jelenségeket részletesen tárgyalta Keglevich László ugyanilyen című, lapunk 1964. dec. számában megjelent cikke.)

A test és a tehetetlenségi nyomatékának kapcsolata

Vizsgáljuk meg most az (5) és (9) összefüggés mondanivalóit közelebbről. Az (5) összefüggés megmutatja, hogy a tömegpont tehetetlenségi nyomatékának nagysága a tömegpont

m

tömegével az

r

tengelytől mért távolság négyzetével egyenesen arányos. Testek pontjainak járulékaira (9) miatt ugyanez érvényes. Ennek ismeretében a forgó mozgást végző testek tehetetlenségi nyomatékát megfelelően változtatni tudjuk, amint azt az előbbi lendítőkerék példánál már láttuk is. Ezen ismereteket alkalmazzák tudatosan vagy ösztönösen az akrobaták és sportolók is. Még lényegesebb azonban a következő. Mivel a pontok tömege és a tengelytől mért távolsága, tehát a tengely körüli tömegeloszlás erősen megszabja a tehetetlenségi nyomaték értékét, ezért a tengely helyét a testhez képest mindig meg kell adni. Ugyanazon test tehetetlenségi nyomatéka (5) és (9) szerint más és más értékű lehet a test forgástengelyének helyzetétől függően. Pl. egy homogén, hosszúkás rúdnak hosszmenti szimmetriatengelyére vonatkozólag a legkisebb, erre merőleges szimmetria tengelyére ennél nagyobb, végül az utóbbival párhuzamos a rúd szélső pontjában felvett tengelyére vonatkozólag még nagyobb a tehetetlenségi nyomaték értéke. Egészen általánosan tehát egy test tehetetlenségi nyomatékáról csak akkor beszélhetünk, ha konkrétan megadjuk, hogy milyen tengelyre vonatkozik.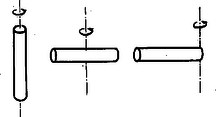

3. ábra

Jelen vizsgálatainkban az ilyen módon értelmezett, tengelyre vonatkozó tehetetlenségi nyomatékkal foglalkozunk. Meg kell azonban jegyeznünk (és ezt Bodó Zalán lapunk 1961. febr. számában megjelent Másodrendű nyomatékok c. cikkében már tárgyalta), hogy használatos a műszaki gyakorlatban ‐ a tengelyre vonatkoztatott tehetetlenségi nyomatékkal kapcsolatban levő ‐ pontra, ill. a síkra vonatkoztatott tehetetlenségi nyomaték fogalma is. A gyakrabban előforduló rögzített tengely körül történő forgó mozgásnál azonban elegendő a tengelyre vonatkoztatott tehetetlenségi nyomaték ismerete. Ezért a továbbiakban csupán erre szorítkozunk és a megkülönböztető jelzőt a középiskolai szokás szerint elhagyjuk.

A tehetetlenségi nyomaték a gyakorlatban

A gyakorlatban a merev testek rögzített tengely körüli forgó mozgása csaknem minden gépi berendezésnél, erőgépnél, meghajtóműnél, munkagépnél, járműnél stb. megfigyelhető. Az egyes termelési, ill. megmunkálási folyamatokat úgy lehet ugyanis folyamatosan gépi úton végeztetni, hogy az ott szükséges mozgásokat forgó mozgássá alakítják. Ezért forog a fúró hegye, a csiszoló-, a keverő-, a daráló-, a szellőztetőgép, az eszterga munkadarabja vagy szerszáma, a malomkő, a körfűrész és a fogorvos is így tudja gépével a szájüreg kis térségében a fogat kezelni. Ha valamely mozgást ismételni kell, mint pl. a nyomdagép műveleteinél, rázó-, présgép esetén, akkor ezt is forgó mozgást végző alkatrészek révén állítják elő. Forgó test a gépek és játékok lendítőkereke, az elektromos generátor forgó része, a lemezjátszó korongja, a magnó tekercse, a körhinta stb. A szárításra használt centrifuga ruhával töltött kosara, a búgócsiga, a sokféle pörgettyű, az űrhajó, a diszkosz, sőt a Föld is pörög maga körül, ez utóbbiak forgástengelye azonban részben vagy egyáltalán nem rögzített. Járműveknél forog a kerék, a lapátkerék, a légcsavar stb. A különböző meghajtóművek tengelyes, fogaskerekes, láncos, futószalagos átvitele is forgó részekkel működik. Ezenkívül a modern erőgépek, a víz- és gőzturbinák, szélkerekek, villamos motorok is mind forgó rendszerűek. Ugyanilyen széles területen alkalmazzák a torziós rendszereket is. (Lásd Keglevich L. említett cikkét.) A felsorolt vagy ezekhez hasonló szerkezetek és gépek forgó alkatrészeinek tengely körüli gyorsulását az (1), munkavégző képességét a (10) összefüggés adja meg, míg a torziós lengéseket (11) jellemzi. Ezek mindegyikében szerepet játszik a tehetetlenségi nyomaték, tehát alkalmazásuknál a forgó részek tehetetlenségi nyomatékát ‐ ha éppen nem ezt keressük ‐ ismerni kell.
A különböző forgó alkatrészekkel kapcsolatos méretezéskor sokféle ilyen kérdés merül fel. Ekkor természetesen még egyéb összefüggéseket is felhasználnak, amelyekben a tehetetlenségi nyomaték szerepel. A gyakorlati feladatok ugyanis a súrlódás, a centripetális erőhatás és a szilárdságtani szempontok figyelembevételét is megkívánják. Az utóbbiakkal azonban itt nem foglalkozunk.
Ilyen terület még a test tehetetlenségi nyomatékának méretezése is. Igen fontos ugyanis az, hogy a tervezők az egyes forgó részek tehetetlenségi nyomatékát még az alkatrész elkészülte előtt méreteik alapján meg tudják határozni, de ugyancsak fontos az is, hogy ezt majd az elkészült alkatrészen mérőkísérlettel ellenőrizni tudják.
Világítsuk meg mindezeket példákkal. Automatikusan működő berendezésekben gyakran alkalmaznak szervomotorokat. Ezek fürge mozgású villamos motorok, amelyek forgásirányukat és sebességüket igen rövid idő alatt meg kell, hogy tudják változtatni. Az előírt szöggyorsulás csak olyan forgó résszel érhető el, amelynek tehetetlenségi nyomatéka (1) összefüggés alapján meghatározható maximális értéknél kisebb. A motorban elérhető forgatónyomaték mellett ez meghatározott tehetetlenségi nyomaték-értéket jelent. Most vagy olyan forgatónyomatékot állítanak elő (pl. megfelelő tekercseléssel), amely a geometriai méretek alapján meghatározott tehetetlenségi nyomatékhoz szükséges, vagy a forgó rész tömegeloszlását alakítják úgy, hogy a kívánt szöggyorsulást a forgatónyomaték biztosítani tudja. Az első esetben a forgó rész tehetetlenségi nyomatékát a helyes forgatónyomaték beállítása miatt kell ismerni, másik esetben pedig annak ellenőrzésére, hogy elérhető-e rajta a tervezett szöggyorsulás.
Nézzünk egy példát a forgó mozgást végző test munkavégzőképességének hasznosításával kapcsolatban is. Lendítőkerék méretezésnél a (10) összefüggés alapján állapítható meg a tehetetlenségi nyomaték azon minimális értéke, amely elegendő ahhoz, hogy a motor és a gőzgép a holtponton túljusson, vagy a játékautó a kívánt távolságon végigfusson. A megengedett maximális geometriai méretek figyelembevételével ezután (9) alapján a megfelelő tömegeloszlás kialakítható, végül pedig a tervek alapján elkészült lendítőkerék tehetetlenségi nyomatékát még méréssel ellenőrizni kell.
Torziós rendszereknél ugyancsak ismerni kell a test tehetetlenségi nyomatékát. Gondoljunk itt példaként az órák billegő kerekére. Természetesen ezeknél van szükség a tehetetlenségi nyomaték értékének legpontosabb ismeretére.
Vizsgáljuk meg ezután, milyen módszerekkel határozható meg a testek tehetetlenségi nyomatéka.

A tehetetlenségi nyomaték meghatározásának módszerei

A testek tehetetlenségi nyomatéka két különböző módon, geometriai vagy kísérleti úton határozható meg. Az első esetben a tehetetlenségi nyomatékot a test tengely körüli eloszlása, ill. geometriai adatai alapján a (9) definíciós összefüggés alkalmazásával határozzuk meg. Az utóbbi esetben viszont a vizsgált testtel olyan mérőkísérletet végzünk, amelyben a tehetetlenségi nyomatéknak szerepe van és az erre érvényes összefüggésben a többi mennyiség könnyen mérhető. Az összefüggésből

I

-t a mért adatok alapján kiszámíthatjuk.

Geometriai módszer: A tehetetlenségi nyomaték pontonkénti járulékainak összegezését a test alakját és tömegeloszlását leíró függvény alapján integrálással számíthatjuk ki. Ezt csak matematikailag jól leírható alakkal és tömegeloszlással rendelkező testekre lehet alkalmazni, és általában az integrál kiszámítása sem könnyű feladat. Sok esetben azonban az integrálás megkerülhető és az

I

érték ‐ pusztán a tehetetlenségi nyomatékra érvényes általános összefüggések felhasználásával ‐ elemi úton is meghatározható. Ezek az összefüggések és a módszerre vonatkozó példák Bodó Zalán már említett cikkében megtalálhatók.
A tehetetlenségi nyomaték meghatározása azonban általában még ennél is egyszerűbb feladat. A legegyszerűbb homogén testek tehetetlenségi nyomatékát a súlyponton átmenő jellegzetesebb tengelyeikre vonatkozólag ugyanis általánosan kiszámították, és az eredményül kapott összefüggéseket táblázatba foglalták. Ezek az összefüggések lehetővé teszik, hogy a testek tömegének és néhány jellegzetes geometriai adatának birtokában a tehetetlenségi nyomatékot igen egyszerűen ‐ képletszerűen ‐ kiszámíthassuk, anélkül, hogy az előbb említett bonyolult számításokat minden esetben elvégeznénk.
A következőkben megadjuk a négy legalapvetőbb ilyen összefüggést, amelyekből a többi egyszerű alak (téglalap, rúd, tárcsa stb.) esetére is könnyen nyerhetünk hasonló képleteket. (Az összefüggések elemi módon való meghatározása néhány kivétellel Bodó Zalán említett cikkében megtalálható.) Mindegyik összefüggés egyenletes tömegeloszlású,

M

tömegű test súlyponton átmenő tengelyére vonatkozik.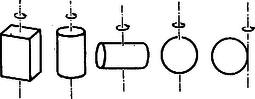

4. ábra

Homogén

M

tömegű téglatest tehetetlenségi nyomatéka a súlyponton átmenő és a

c

éllel párhuzamos tengelyre vonatkozólag

\begin{matrix} I_{c} = \frac{1}{12} M (a^{2} + b^{2}), \end{matrix}

(12)

ahol

a

és

b

a tengelyre merőleges élek hossza. Természetesen bármelyik éllel párhuzamos tengelyre hasonló összefüggés érvényes. (12) alapján a homogén téglalap-, ill. pálcaszerű idomok súlyponton átmenő bármelyik éllel párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka is meghatározható, ha ebben a megfelelő élhosszat nullának vesszük.
Homogén

M

tömegű és

R

sugarú egyenes körhenger tehetetlenségi nyomatéka súlyponton átmenő alkotóval párhuzamos forgástengelyre vonatkozólag

\begin{matrix} I_{H} = \frac{1}{2} M R^{2}, \end{matrix}

(13)

és ugyanennek a tehetetlenségi nyomatéka a súlyponton átmenő előbbire merőleges tengelyre

\begin{matrix} I_{H'} = M (\frac{1}{4} R^{2} + \frac{1}{12} h^{2}), \end{matrix}

(14)

ahol

h

a henger magasságát jelenti. Az utóbbi összefüggésből a körtárcsa súlyponton átmenő tengelyére vonatkozó tehetetlenségi nyomatékát is meghatározhatjuk, ekkor ugyanis

h = 0

.
Végül a homogén

M

tömegű

R

sugarú gömb tehetetlenségi nyomatéka a súlyponton átmenő tengelyére vonatkozólag

\begin{matrix} I_{G} = \frac{2}{5} M R^{2} . \end{matrix}

(15)

A felsorolt vagy ezekhez hasonló összefüggések megfelelő kombinálása révén részekre bontás útján, ill. megfelelő tengelyáthelyezéssel természetesen összetettebb esetekben is célhoz jutunk. (9) szerint ugyanis azonos tengelyre nézve a tehetetlenségi nyomaték egyszerűen összegezhető skaláris mennyiség, továbbá a Steiner-tétel alapján (lásd Bodó Z., ill. Keglevich L. említett cikkét) párhuzamos tengelyáthelyezések is igen egyszerűen elvégezhetők. A Steiner-tétel szerint

\begin{matrix} I = I_{s} + m s^{2}, \end{matrix}

(16)

vagyis az

I

súlyponton átmenő tengellyel párhuzamos tengelyre vett tehetetlenségi nyomatékot megkapjuk, ha a súlyponton átmenő tengelyre vonatkozó

I_{s}

tehetetlenségi nyomatékhoz hozzáadjuk a test

m

tömegének és a két tengely közti

s

távolság négyzetének szorzatát.
A tétel alkalmazását egy példán mutatjuk be. Határozzuk meg a gömb egy érintőjére mint tengelyre vonatkozó tehetetlenségi nyomatékát. Ez a Steiner-tétel szerint és (15) alapján

\begin{matrix} I_{t} = \frac{2}{5} M R^{2} + M R^{2} = \frac{7}{8} M R^{2} \end{matrix}

(17)

lesz. A tételből mindenesetre az is látszik, hogy a súlyponton átmenő tengelyre vonatkozólag a test tehetetlenségi nyomatéka a legkisebb.
A geometriai módszer feltételezi az egyenletes vagy matematikailag jól leírható tömegeloszlást, az idealizálható és matematikailag könnyen leírható alakot, továbbá lehetőséget a tömeg és geometriai adatok mérésére. Ez a gyakorlatban nem mindig teljesül. Bonyolultabb alakú és tömegeloszlású testekre a geometriai módszer nem is alkalmazható. Előnye viszont mégis az, hogy az

I

érték becslésére az alkatrész elkészítése előtt már a tervezésnél lehetőséget ad, mégpedig a leggyakoribb esetekben igen egyszerűen. Mérési pontossága pedig gyakorlatilag csak a geometriai adatok mérési pontosságától függ. Ezek ugyanis egyrészt a képletben magasabb hatványon szerepelnek, másrészt a tömeg amúgy is nagy pontossággal mérhető, vagy ha azt a sűrűség alapján határozzuk meg, a geometriai adatok a tömeghez is szükségesek. Ezért a geometriai adatokat mindig nagyszámú, a test különböző helyzetében elvégzett mérésből kell megállapítani, hogy a test görbületei és képlékenysége, továbbá a felületének érdessége által okozott hibák a minimálisak legyenek.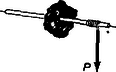

Kísérleti módszer: A tehetetlenségi nyomaték meghatározásának másik útja a mérőkísérlet. Ez lehetővé teszi bármilyen szabálytalan és inhomogén test tehetetlenségi nyomatékának meghatározását is, továbbá a geometriai úton kiszámolt

I

érték ellenőrzését, akkor is, ha a testről semmiféle adat nem áll rendelkezésre. A módszer azon alapul, hogy a testtel mérőkísérletet végzünk, és a kísérlet során nyert adatokból az ilyenkor érvényes összefüggés segítségével

I

-t kiszámítjuk. Ilyen mérésre alkalmas kísérlet a test tengely körüli gyorsítása és torziós lengése.

A tehetetlenségi nyomaték meghatározása tengely körüli gyorsítás alapján: A tehetetlenségi nyomatékot a test tengely körüli gyorsítása esetében lényegében az (1) összefüggéssel határozzuk meg. Ezért a mérendő testet a szóban forgó tengely mentén csapágyazzuk, és az ismert állandó forgatónyomaték hatására rajta bekövetkező szöggyorsulást mérjük. Ismert állandó forgatónyomatékot úgy állíthatunk elő, hogy az

r

sugarú tengelyre fonalat csévélünk, és ezen állandó

P

húzóerőt fejtünk ki.

5. ábra

A szöggyorsulás meghatározása állandó

F

forgatónyomaték esetén időmérésre vezethető vissza az egyenletesen változó mozgásnál ismert

\begin{matrix} a = \frac{2 s}{t^{2}} \end{matrix}

(18)

összefüggés alapján (ebben

s

a letekeredett szál hosszát,

a

a kerületi gyorsulást és

t

a gyorsítás idejét jelenti). Ilyen módon a tehetetlenségi nyomaték értékére (1), (3) és (18) figyelembe vételével a következőt nyerjük:

\begin{matrix} I = \frac{F}{β} = \frac{P \cdot r}{a / r}, tehát I = \frac{P t^{2} r^{2}}{2 s} . \end{matrix}

(19)

Ezzel

I

meghatározását alapmennyiségek mérésére vezettük vissza. Eredményünkből láthatjuk, hogy e módszernél a test tehetetlenségi nyomatékának meghatározásához a húzóerőt, a letekeredett szál hosszát, a tengely sugarát és az erőhatás idejét kell mérni. Elsősorban az

r

és

t

értékek pontosságától függ a mérés pontossága, mivel az összefüggésben négyzetesen szerepelnek. Ezeket tehát fokozott pontossággal kell mérni. A módszer előnye, hogy magán a testen semmit sem kell mérni, tetszőleges alakú és tömegeloszlású lehet. A geometriai módszerhez képest azonban több adat mérését igényli. Hátrányos továbbá az is, hogy éppen a könnyen mérhető kisebb szöggyorsulás esetében számottevő a súrlódás hatása és a gyorsító szerkezet esetleg együtt mozgó részei is módosíthatják a tényleges értékeket. Általában mindkettő, de főként az utóbbi körülmény számítással elég jól követhető. Az így nyert módosított összefüggések alapján mérési eredményeink most már helyes értéket adnak.

6. ábra

Nézzük meg például azt az esetet, amikor az ismert forgatónyomatékot a tengelyre csévélt fonál másik végére függesztett súllyal állítjuk elő. Ekkor a mérés alatt a súly maga is gyorsulni fog és ez húzóerejét állandóan csökkenti. Ekkor is könnyen megkapjuk azonban az eredményt, ha az energiamegmaradás elvét alkalmazzuk. Eszerint a súly helyzeti energia-vesztesége egyenlő a súly és forgórész együttes mozgási energiájával:

\begin{matrix} m g s = \frac{m v^{2}}{2} + \frac{I ω^{2}}{2}, \end{matrix}

(20)

ahol

m

a súly tömege,

g

a nehézségi gyorsulás,

v

a súly pillanatnyi sebessége és

ω

a forgórész pillanatnyi szögsebessége. Tudjuk, hogy az egyenletesen gyorsuló mozgás esetében

\begin{matrix} v = \frac{2 s}{t}, \end{matrix}

(21)

továbbá ‐ mivel a fonál nem nyúlik ‐

v = r \cdot ω

, tehát az energia megmaradását leíró egyenlet úgy alakítható át:

\begin{matrix} m g s = \frac{2 m s^{2}}{t^{2}} + I \frac{2 s^{2}}{r^{2} t^{2}} . \end{matrix}

(22)

Ebből a forgó test tehetetlenségi nyomatéka

\begin{matrix} I = \frac{G t^{2} r^{2}}{2 s} - m r^{2}, \end{matrix}

(23)

ha a húzóerőt

G

-vel jelöljük. Látjuk, hogy az előbbihez képest összefüggésünk a

(- m r^{2})

taggal bővült. Ebben azonban új mérnivaló nincs, hiszen a súly

G

húzóereje tömegét is meghatározza. Ha a súly tömege kicsi a testéhez képest, a (19) összefüggés továbbra is jó közelítés marad. Hasonlóan lehet a fonál irányát megváltoztató csigát, a súrlódást stb. is figyelembe venni. Ha még pontosabb

I

értékeket szeretnénk nyerni, más módszert, a torziós lengések módszerét kell alkalmaznunk.
A tehetetlenségi nyomaték meghatározása torziós lengések alapján: Az előbbiekben (11) láttuk, hogy a tehetetlenségi nyomaték a torziós lengéseknél is szerepet játszik, meghatározása tehát ennek alapján is lehetséges. Ez esetben a testet torziós szálra erősítjük úgy, hogy a szál iránya és a test szóban forgó vonatkoztatási tengelye egybeessék. Így a rendszer mint torziós inga lengéseket végezhet.

7. ábra

A lengés idejére érvényes (11) összefüggésben azonban a mérés szempontjából célszerű a

D^{*}

-t a torziós rugalmassággal kapcsolatos ismeretek alapján, a szál

G

torziómoduluszával,

l

hosszával és

r

sugarával kifejezni, így a

\begin{matrix} T = 2 π \sqrt[]{\frac{2 l I}{G r^{4} π}} \end{matrix}

(24)

száladatokat tartalmazó lengésidő képletet nyerjük. (Lásd Keglevich László idézett cikkét.) Ebből pedig

I

-t kifejezve

\begin{matrix} I = \frac{G r^{4}}{8 π l} T^{2} . \end{matrix}

(25)

A tehetetlenségi nyomatékot meghatározhatjuk tehát a

T

lengésidő mérésével,

l

r

és

G

ismeretében. Ilyen módon azonban az egész rendszer együttes tehetetlenségi nyomatékát kapjuk meg. Ez csak viszonylag nagy testek esetén ad kielégítő eredményt, mivel ekkor a szál és a felfüggesztő rendszer tehetetlenségi nyomatéka a testéhez képest elhanyagolható.
A test

I_{1}

tehetetlenségi nyomatéka természetesen a felfüggesztő rész

I_{ü}

tehetetlenségi nyomatékának elhanyagolása nélkül pontosan is meghatározható. Ehhez azonban az ismeretlennel terhelt

T_{1}

lengésidő mérésén kívül mérni kell az üres inga

T_{ü}

lengésidejét is. Az üres inga

T_{ü}

lengésideje (24) szerint

\begin{matrix} T_{ü} = 2 π \sqrt[]{\frac{2 l I_{ü}}{G r^{4} π}}, \end{matrix}

(26)

az ismeretlennel terhelt inga lengésideje pedig (9) figyelembe vételével

\begin{matrix} T_{1} = 2 π \sqrt[]{\frac{(2 l I_{ü} + I_{1})}{G r^{4} π}} . \end{matrix}

(27)

A két lengésidő négyzetének a különbsége

\begin{matrix} T_{1}^{2} - T_{ü}^{2} = \frac{4 π^{2} \cdot 2 l}{G r^{4} π} I_{1} . \end{matrix}

(28)

Ebből

I_{1}

tehetetlenségi nyomaték értékét kifejezve megkapjuk a keresett

\begin{matrix} I_{1} = \frac{G r^{4} (T_{1}^{2} - T_{ü}^{2})}{8 π l} \end{matrix}

(29)

összefüggést. Ez most már a mérendő test tényleges tehetetlenségi nyomatékát adja meg. (25) és (29) összehasonlításából láthatjuk, hogy

T_{1}

hez képest kis

T_{ü}

lengésidejű inga esetén (25) jó közelítést ad.
A tehetetlenségi nyomatékot száladatok nélkül is megállapíthatjuk. A száladatok helyett azonban ekkor meg kell határoznunk egy ismert

I_{2}

tehetetlenségi nyomatékú test felfüggesztése esetén az inga

T_{2}

lengésidejét. Az utóbbi esetre ugyanis szintén felírható a (29)-hez hasonló összefüggés:

\begin{matrix} I_{2} = \frac{G r^{4} (T_{2}^{2} - T_{ü}^{2})}{8 π l} . \end{matrix}

(30)

A kettő hányadosa pedig máris szolgáltatja az új, csupán a lengésidőket és az ismert tehetetlenségi nyomatékot tartalmazó összefüggést:

\begin{matrix} I_{1} = I_{2} \frac{T_{1}^{2} - T_{ü}^{2}}{T_{2}^{2} - T_{ü}^{2}} . \end{matrix}

(31)

E módszer komoly előnye, hogy a száladatok helyébe a nagy pontossággal mérhető lengésidő értékek és megfelelő testet választva az igen pontosan meghatározható

I_{2}

tehetetlenségi nyomaték kerül.
Az összefüggést tovább egyszerűsíthetjük, ha rögzített tengellyel rendelkező rendszereken végezzük a mérést. Gépek forgórészeinek tehetetlenségi nyomatékát pl. ilyen módon mérik. A mérés során az óra billegőjéhez hasonló módon egy nagy spirálrugó segítségével a forgórészt lengésbe hozzák és megmérik a lengésidőt, majd

I_{2}

ismert tehetetlenségi nyomatékú test odaerősítése után a lengésidő mérését megismétlik. A (31) összefüggés ekkor a (26‐31) gondolatmenet megismétlésével így egyszerűsödik:

\begin{matrix} I_{1} = I_{2} \frac{T_{1}^{2}}{T_{2}^{2} - T_{1}^{2}} . \end{matrix}

(32)

Ezen mérésnél ügyelni kell arra, hogy a rugó tömege a forgórészhez képest elhanyagolható legyen, mert különben hatását a (31)-nél említett módon külön figyelembe kell venni.

8. ábra

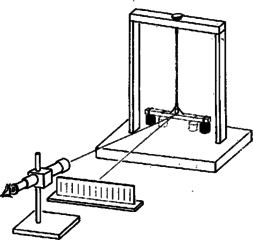A torziós módszereket összefoglalva megállapíthatjuk, hogy ezeknél a mérendő mennyiségek száma az előbbi módszerekhez viszonyítva általában nagyobb. Ezek közül a legnagyobb problémát a torziós szál

r

sugarának mérése jelenti, mivel az összefüggésben a negyedik hatványon szerepel és ugyanakkor még a legjobb szálkivitel esetén is a szál különböző pontjain az elérhető mérési pontosságnál jóval nagyobb mértékben ingadozik.

G

meghatározása több mennyiség mérésén alapuló elég komoly külön mérési feladat. (Lásd Keglevich L. említett cikkét.) E nehézségek azonban megkerülhetők, mivel vannak olyan összefüggéseink (31) és (32), amelyekben száladatokra nincs szükség. Ezekben ugyanis a száladatok meghatározását a lengésidő mérésre vezetjük vissza azáltal, hogy az ismeretlen tehetetlenségi nyomatékot ismert tehetetlenségi nyomatékhoz viszonyítjuk.
A torziós módszerek előnye pedig éppen abban rejlik, hogy a tehetetlenségi nyomaték meghatározására jórészt az egyszerűen és igen pontosan mérhető lengésidő mérések alapján ad lehetőséget. Ezzel kapcsolatban azonban nem lehet eléggé hangsúlyozni, hogy a tehetetlenségi nyomaték megállapításához valóban nagyon pontos lengésidő értékekre van szükség. Ez kitűnik abból, hogy az összefüggésekben a lengésidők négyzetei szerepelnek és ezeknek is a különbségét kell képezni. A lengésidő azonban sok lengés alapján igen nagy pontossággal mérhető, és ezért a tehetetlenségi nyomaték mérését a legnagyobb pontossággal a torziós módszerrel végezhetjük el.