| Cím: | A Brown-mozgás | ||
| Szerző(k): | Vesztergombi György | ||
| Füzet: | 1965/november, 161 - 167. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Bevezetés Képzeljük magunkat az angol botanikus, Robert Brown (1827) helyébe, aki mikroszkópjába tekintve állítólag először figyelt fel az oldatban lebegő apró festékszemcsék ide-oda cikázó mozgására. Mint az élővilágot tanulmányozó tudóstól nem állhatott tőle távol az a gondolat, hogy valami kis mikroszkopikus élőlényektől származik ez az örökös mozgás, aminek persze rögtön ellentmondott a részecskék minden életmegnyilvánulást nélkülöző anyagból való eredete. Ma már az ilyen és ehhez hasonló elképzeléseken csak nevetünk, de azért most is felmerülhet a kétely: hogyan lehet az, hogy ezek a részecskék a tapasztalat szerint mindig fellépő súrlódás ellenére örökös mozgásban vannak. Honnan veszik ehhez az energiát? Talán valami belső energiaforrás pótolja a veszteségeket? Ez a feltevés még az előzőnél is rosszabb, mert ezzel az energiamegmaradással kerülnénk szembe, ugyanis minden Brown-részecskét az örökmozgó egy-egy mintapéldányának tekinthetnénk. Az ellentmondás eltűnik, ha elfogadjuk az anyag molekulár-kinetikus elméletét. Eszerint minden anyag igen apró, kb. cm átmérőjű, mikroszkópon nem látható, állandóan rendszertelen mozgásban levő molekulákból áll. Ezek között per definitionem nem lép fel súrlódás, hisz a makroszkópikus testek súrlódásakor hő formájában elvont energia éppen ezen molekulák kinetikus energiájának növelésére fordítódik. Nézzük meg, hogyan magyarázható a molekulár-kinetikus elmélet alapján a Brown-részecskék mozgása. Ha folyadékba vagy gázba makroszkopikus test merül, a rendszertelen mozgásban levő molekulák ütköznek a test felületén és eközben erőt fejtenek ki a szilárd testre. A molekulák ütközése a test felületén minden oldalról teljesen rendszertelenül történik. Ha a test lineáris méretei elég nagyok, úgyhogy már rövid idő alatt is sok molekula ütközik a test felületén, akkor a molekulák ütközése folytán a különböző irányokból nyert lökések kompenzálják egymást, vagyis a test nyugalomban marad. Ha ellenben a közegben elég kis méretű részecskék lebegnek (maximális lineáris méret kb. cm), pl. tust cseppentünk a vízbe, akkor a különböző irányú lökések már nem fognak közepelődni, a részecske rendkívül szaporán fogja sebességének irányát és abszolút értékét változtatni (másodpercenként kb. -szer): Emiatt a részecske tényleges mozgását nyomon követni; és a mozgás irányváltozásainak helyét rögzíteni lehetetlen. Szemünkkel csak a pálya kivonatát tudjuk megfigyelni, és ami így látszólag egyenes szakasz, a valóságban szubmikroszkópikus cikcakkok milliárdjaiból tevődik össze. Ez azonban, mint azt később látni fogjuk, nem változtat a jelenség lényegén. Ezek alapján a Brown-mozgás roppant meggyőző érvet szolgáltat az atomelmélet mellett, de bizonyító erejűvé akkor válik, ha a kvalitatív meggondolások mellett kvantitatív összefüggésekre is vezet. Az ezzel kapcsolatos számításokat elősször Einsteinnek és Smoluchowskinak sikerült 1906-ban elvégeznie. A következőkben lényegében az ő gondolatmenetüket követve megmutatjuk, hogy a Brown-mozgás alapján meghatározható az Avogadro-szám (a molnyi mennyiségben levő molekulák száma), amivel azt is illusztrálhatjuk, hogy azért a véletlennek is vannak törvényei. 2. A ,,bolyongás'' probléma Nyilvánvaló, hogy ezen a fokon a számítást teljes általánosságban képtelenség nemcsak elvégezni, de még követni is. Ezért a jelenség lényeges momentumait kiragadva próbáljunk egy szemléletes modellt szerkeszteni. A Brown-részecskék mozgását az jellemzi, hogy a részecske az -edik és az -edik ütközés között egyenes vonalú egyenletes mozgással utat tesz meg. A továbbiakban tegyük fel, hogy a) csak egy egyenes mentén történik ez az elmozdulás egyenlő valószínűséggel jobbra vagy balra, vagyis korlátozódjunk egydimenziós mozgásra; b) a két ütközés között megtett utak hossza legyen azonos, egyelőre tekintsük ezt hosszegységnek; c) a két ütközés között eltelt idő is legyen azonos (); d) időpillanatban legyen a Brown-részecske az origóban. Ezek után kérdezhetjük, hogy körülbelül milyen messzire lesz ütközés után, azaz időpillanatban a részecske az origótól; vagy másképp: mi annak a valószínűsége, hogy -kor pont egységnyi távolságra lesz az origótól. Ezt a problémát a valószínűségszámításban a ,,bolyongás'' problémájának szokás nevezni. Már többször említettük a titokzatos ,,valószínűség'' szót, de eddig tartózkodtunk annak mélyrehatóbb elemzésétől. Ez a fogalom a modern matematikába teljes egzaktsággal bevezethető, sőt a valószínűségi jelenségekkel foglalkozó vizsgálatok a matematika egyik legrohamosabban fejlődő fejezetét alkotják. De a valószínűségnek nemcsak ilyen elméleti jelentősége van, hanem centrális szerepet tölt be jóformán az egész fizikában. Ugyanis a fizikus számára egy adott esemény bekövetkezésének valószínűsége ugyanolyan reálisan létező fizikai mennyiség, mint például egy rúd hossza, csak éppen kissé nehezebben hozzáférhető jellemzője a fizikai objektumoknak (bár éppen a véletlen ingadozások és egyéb pontatlanságok miatt sokszor a precíz hosszúságmérés sem jelent sokkal egyszerűbb feladatot, és a hiba, azaz a statisztikus ingadozás mértékének megadása nélkül nem is igazi mérés a mérés). A valószínűség fogalma a mindennapi élet tapasztalatain alapul. Hiszen minden cselekedetünket a valószínűség szélső eseteinek alapulvételével végezzük. Akkor megyünk át az utcán, amikor igen valószínűnek látszik, hogy nem gázol el bennünket valamilyen jármű, de mint a közlekedési balesetek bizonyítják, nem -ig biztos, hogy baj nélkül juthatunk át a túloldalra. A Brown-részecskék mozgásának az egydimenziós bolyongási problémára való specializálásával elértük azt, hogy az adott esetre vonatkozóan kielégítő definíciót adjunk az egyes események bekövetkezésének valószínűségére vonatkozóan. Vizsgáljuk a részecske első Ezért ennek valószínűsége: Ezzel a definícióval felvértezve most már hozzáfoghatunk annak a kiszámításához, hogy mennyi annak a valószínűsége, hogy A kedvező esetek száma tehát megegyezik azon elemi események számával, amelyekben Ide Tegyük fel, hogy az origóba tett részecskével a kísérletet nagyon sokszor ( Határozzuk meg a bolyongási probléma várható értékét: A szummákból kiemelve a konstans faktorokat, az első szummában elegendő A binomiális együtthatók összege éppen egyenlő E hosszadalmas számítás elég triviális eredményre vezetett, tudniillik azt mondja, kogy a részecske állandóan az origó körül fog ugrándozni. Persze ez nem jellemzi eléggé a mozgást, mert így az origótól való eltérés átlagos nagyságáról nem kaptunk semmiféle tájékoztatást. Ennek oka abban keresendő, hogy az elmozdulásokat előjelesen átlagoltuk. Ezen a hibán segíthetnénk úgy, hogy az eltávolodás abszolut értékének a várható értékét határoznánk meg. Matematikailag azonban sokkal könnyebben járható út, ha az elmozdulás négyzetének várható értékét határozzuk meg, ami szintén elhárítja a fenti nehézséget. Definíció szerint: Az előzőhöz hasonló, csak pár lépéssel hosszabb számolás alapján adódik: Ezt a formulát az a körülmény teszi rendkívül használhatóvá, hogy Eddigi meggondolásaink csak az egydimenziós esetre vonatkoztak. Most térjünk át a háromdimenziós térben mozgó részecskére. Tudjuk, hogy minden háromdimenziós elmozdulás összetehető három kiválasztott tengely irányában történt elmozdulásból. Ha olyan kísérleti körülményeket választunk, hogy a térben nincs kitüntetett irány, akkor az egyes irányokba való elmozdulások azonos törvényszerűségeket követnek, vagyis mindhárom irányra nézve az elmozdulások négyzetének várható értéke: 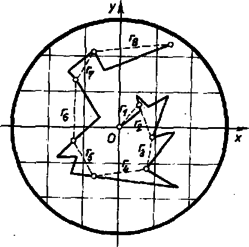 Mivel az túlságosan kényelmetlen lenne, hogy minden egyes méréshez a részecskét vigyük az origóba, ezért ,,Mohamed megy a hegyhez'' alapon, minden Ebből az előző képlet alapján: A méréseket Perrin, francia fizikus elvégezte és tényleg jó egyezést talált a más úton levezetett kb. 3. A Brown-mozgás általánosítása Képzeljük el, hogy a Brown-féle részecske méreteit egyre csökkentjük. Mivel a fenti meggondolásokban a részecske speciális tulajdonságait sehol sem használtuk fel, ezért azok érvényesek lesznek még akkor is, ha a szétdarabolásban egészen a molekulákig jutunk el. Vagyis a gáz vagy a folyadék molekulái is Brown-mozgást végeznek! Itt aztán igazán teljesül az a feltétel, hogy egy adott időpillanatban a különböző oldalról való ütközések nem kompenzálják egymást. Persze ez a mozgás még a legjobb mikroszkóppal is megfigyelhetetlen egyrészt a molekulák roppant kis méretei, másrészt az igen nagy sebességek miatt. Ugyanis a molekulák átlagos sebessége több mint Másik általánosítási lehetőségként a következő mód kínálkozik. Eddig egyetlen kiszemelt Brown-részecske, ill. molekula mozgására vonatkozó törvényszerűségeket tanulmányoztunk. Most tekintsünk nagyon sok részecskét. Vegyünk két gázzal töltött edényt, amelyeket kezdetben az 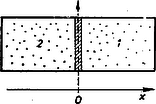 Ekkor az |