Az I. forduló feladatai:

 

1. ábra

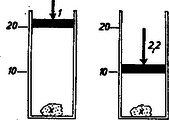xcm3, akkor az első állapotban 1 atmoszférás nyomás mellett a levegő térfogata $\left(20-x\right){\text{cm}}^3$. A végállapotban a nyomás $2\mathrm{,}2$ atmoszféra, és az ugyanakkora tömegű levegőnek a térfogata $\left(10-x\right){\text{cm}}^3$. A nyomás és tétfogat szorzata állandó:

$\begin{array}{c}{\displaystyle 1\cdot \left(20-x\right)=2\mathrm{,}2\cdot \left(10-x\right)\mathrm{.}}\end{array}$

Ebből az egyenletből a porózus anyag térfogatára kapjuk:

$\begin{array}{c}{\displaystyle x=1\mathrm{,}67{\text{cm}}^3\mathrm{.}}\end{array}$

Az eljárás elvben arra alkalmas, hogy porózus anyagok (szivacs, homok) anyagának valódi térfogatát meghatározzuk. Az eljárás pontossága nem nagy.

 

2. Valaki kerékpárja első kerekének tehetetlenségi nyomatékát úgy akarja meghatározni, hogy
a) a kereket tengelyén teljesen kiegyensúlyozza (a kerék a tengelyen minden helyzetben egyensúlyban marad),
b) a kerék küllőjére a forgásponttól $l$ távolságra $m$ tömegű, pontszerűnek tekinthető ólomnehezéket erősít,
c) a kereket lengésbe hozza és megméri a $T$ lengésidőt.
Megkaphatja-e ezekből az adatokból a keresett tehetetlenségi nyomatékot? Mekkora ez, ha 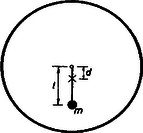$m=0\mathrm{,}5\text{kg}$, $l=0\mathrm{,}2\text{m}$ és $T=1\mathrm{,}2\text{sec}$?

 

 

2. ábra

 

Megoldás. A kerék tömege eredetileg $M$, tehetetlenségi nyomatéka $I$. Ha ráerősítjük $l$ távolságban az $m$ tömeget, az együttes tömeg $M+m$, az együttes tehetetlenségi nyomaték $I+m{l}^2$, és a súlypontnak a tengelytől mért távolsága $d$ lesz (2. ábra). Az ilyen módon létrejött fizikai inga lengésideje:

$\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{I+m{l}^2}{\left(M+m\right)gd}}\mathrm{.}}\end{array}$

Ki kell számítanunk a $d$ súlyponttávolságot. Az erre szolgáló aránypár:

$\begin{array}{c}{\displaystyle d:\left(l-d\right)=m:M\mathrm{,}}\end{array}$

innen:

$\begin{array}{c}{\displaystyle d=\frac{m}{M+m}\cdot l\mathrm{.}}\end{array}$

Behelyettesítve ezt a lengésidő képletébe, $M+m$ kiesik és kapjuk:

$\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{I+m{l}^2}{mgl}}\mathrm{.}}\end{array}$

Tehát a kerék tömegének ismerete nélkül kapjuk meg a tehetetlenségi nyomatékot; eredményünket rendezve:

$\begin{array}{c}{\displaystyle I=mgl{\left(\frac{T}{2\pi }\right)}^2-m{l}^2\mathrm{.}}\end{array}$

A megadott számadatokkal a kerék eredeti tehetetlenségi nyomatéka:

$\begin{array}{c}{\displaystyle I=157700\text{gr}\cdot {\text{cm}}^2=0\mathrm{,}01577\text{kg}\cdot {\text{m}}^2\mathrm{.}}\end{array}$

3. $1\text{cm}$ sugarú gömböt $900\text{V}$ feszültségre töltünk fel. A gömböt $30\text{cm}$ hoszszú szigetelő nyélre helyezve $18000/\text{perc}$ fordulatszámmal megforgatjuk. Mekkora mágneses térerő észlelhető a forgástengely helyén? (A forgó kis gömböt a mágneses tér meghatározásához tekintsük pontszerű töltésnek.) A körvezető középpontjában a mágneses térerősség $H=\frac{I}{2r}\left(\frac{\text{A}}{\text{m}}\right)$.

 

Megoldás. Először meg kell határoznunk, mennyi a kis gömbben levő töltés. A gömb kapacitása arányos rádiuszával; ha $R$ rádiuszt cm-ben, $C$ kapacitást faradban mérjük, akkor $C=R/9\cdot {10}^{11}$. Tehát az 1 cm-es gömb kapacitása $C=1\mathrm{,}11\cdot {10}^{-12}\text{farad}=1\mathrm{,}11\text{pF}$. A gömb töltése 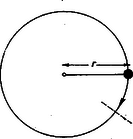$Q=CU$ alapján $Q=1\mathrm{,}11\cdot {10}^{-12}\cdot 900={10}^{-9}\text{coulomb}=1\text{nC}$.

 

 

3. ábra

 

A kör mentén körülvitt töltés köráramot jelent (3. ábra). A percenként 18 000-es fordulatszám 1 másodperc alatt 300 fordulat, tehát a körpálya valamely pontján az 1 nC 1 másodperc alatt 300-szor halad át és így a mozgatott töltés mágneses hatása olyan, mint az $I=300\cdot 1\cdot {10}^{-9}=3\cdot {10}^{-7}\text{amper}=0\mathrm{,}3\mu A$ erősségű elektromos áramé.
A köráram középpontjában jelentkező mágneses térerősségre megadott képlet szerint $H=3\cdot {10}^{-7}/2\cdot 0\mathrm{,}3=5\cdot {10}^{-7}\text{A/m}$. (Ha a mágneses térerősséget a $0\mathrm{,}2\pi I/r$ képlettel számítjuk ki, akkor $H=0\mathrm{,}2\pi \cdot 3\cdot {10}^{-7}/30=6\mathrm{,}28\cdot {10}^{-9}$ oersted.)

 

A II. forduló feladatai

 

1. Felfüggesztett $L$ hosszúságú rugóra olyan kisméretű testet akasztunk, amely a rugót eredeti hosszának $c$-szeresével nyújtja meg ($l=cL$). A rugót a testtel együtt vízszintes helyzetbe hozzuk (a rugó ekkor nyújtatlan állapotban van, hossza $L$), és innen elengedjük. Mekkora a rugó megnyúlása, amikor a test éppen a felfüggesztési pont alatt halad át?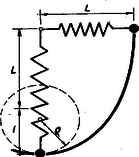

 

 

4. ábra

 

Megoldás. Az eredetileg $L$ hosszúságú rugó $l$ megnyúlása arányos az $L$ eredeti hosszal és a $P$ nyújtó erővel: $l=eLP$; a feladat szövegében szereplő állandó $c=eP$. Az $l$ megnyúlást okozó erő $P=l/eL$. Az induláskor $L$ hosszúságú rugó hossza a felfüggesztési pont alatt való áthaladáskor $L+l$, ezalatt az $m$ nagyságú tömegnél a nehézségi erő munkavégzése $mg\left(L+l\right)$, (4. ábra).
Ha a felfüggesztési pont alatt $v$ sebességgel halad át a tömeg, akkor mozgási energiája $m{v}^2/2$. A megnyúlt rugóban rugalmas energia van elraktározva. A nyújtáshoz szükséges munkavégzés $L$ úton történt 0-ról $l/eL$-re lineárisan növekvő erővel szemben, ezért középértékben az erő felét véve számításba a rugó nyújtásához szükséges munkavégzés:

$\begin{array}{c}{\displaystyle \frac{1}{2}\cdot l\cdot \frac{l}{eL}=\frac{l^2}{2eL}\mathrm{.}}\end{array}$

A mechanikai energiamegmaradás törvénye szerint a nehézségi erő munkája egyenlő a megszerzett mozgási energia és a rugalmas erővel szemben végzett munka összegével:

$\begin{array}{c}{\displaystyle mg\left(L+l\right)=\frac{m{v}^2}{2}+\frac{l^2}{2eL}\mathrm{.}}\end{array}$

Ebben az egyenletben $l$ és $v$ az ismeretlenek.
Amikor a mozgó tömeg függőlegesen a felfüggesztési pont alatt van (és vízszintes irányban halad), akkor a rugó ereje szolgáltatja az $mg$ súly ellenerejét és a centripetális erőt: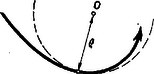

$\begin{array}{c}{\displaystyle \frac{l}{eL}=mg+\frac{m{v}^2}{\varrho }\mathrm{.}}\end{array}$

Itt $\varrho$ a pálya görbületi sugara. Tehát ebben az egyenletben három ismeretlen van: $l$, $v$ és $\varrho$.

 

 

5. ábra

 

Ha egy tömeg görbe pályán mozog, akkor az centripetális erő $m{v}^2/\varrho$. $\varrho$ a görbületi sugár, azon kör rádiusza, amely az illető helyen legpontosabban simul a görbéhez (5. ábra). (A görbületi kör fogalma megtalálható például a Középiskolai Matematikai Lapok 1964. évi 3. számában a 129. oldalon kezdődő cikkben.) Feladatunkban a kérdezett pontban ismeretlen a görbületi sugár értéke, ezért a feladatot nem tudjuk megoldani. Az a gondolat, hogy a kérdéses pontban a görbületi sugár $L+l$ volna, minden alapot nélkülöz. Nagyon is kérdéses, hogy a görbületi középpont egyáltalán benn van-e a felfüggesztési ponton átmenő függőlegesben, amikor a tömeg ezen áthalad, vagyis, hogy a tömeg vízszintesen halad-e át a felfüggesztési pont alatt. Adott numerikus értékek mellett, hosszadalmas számítási eljárásokkal a tömeg pályája bizonyos közelítéssel megállapítható.

 

2. A száloptikás orvosi tükör (endoszkóp) optikai modellje adott $n_1$ törésmutatójú szál, amelyet oldalról $n_2$ törésmutatójú anyag vesz körül. A szál vége síklap, amely $n_3$, törésmutatójú közeggel érintkezik. (A törésmutatók levegőre vonatkoznak.) Hogyan kell $n_1$ értékét megválasztanunk ahhoz, hogy a szálon keresztül a véglap alatti teljes félteret láthassuk, ha a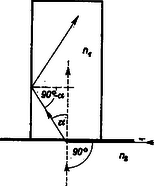) $n_2=n_3=1$, b) $n_2=1$ és $n_3=4/3$?

 

 

6. ábra

 

Megoldás. Vegyük figyelembe azt a határesetet, amikor a fénysugár az $n_3$ törésmutatójú anyagból súrlódva érkezik a határfelületre és az $n_1-n_2$ határfelületet a teljes visszaverődés határszöge alatt érinti (6. ábra). $\alpha$ az $n_1$ törésmutatójú közegbe belépő sugár irányát jelzi. Az $n_3-n_1$ határfelületen:

$\begin{array}{c}{\displaystyle \frac{\text{sin}{90}^{\circ }}{\text{sin}\alpha }=\frac{n_1}{n_3};}\end{array}$

a teljes visszaverődés határesetének feltétele az $n_1-n_2$ határfelületen:

$\begin{array}{c}{\displaystyle \frac{1}{\text{sin}\left({90}^{\circ }-\alpha \right)}=\frac{n_1}{n_2}\mathrm{.}}\end{array}$

Mivel $\text{sin}{90}^{\circ }=1$ és $\text{sin}\left({90}^{\circ }-\alpha \right)=\text{cos}\alpha$, ezért $\text{sin}\alpha =n_3/n_1$ és $\text{cos}\alpha =n_2/n_1$. $\alpha$ kiküszöbölése leggyorsabban a négyzetek összegezésével történik:

$\begin{array}{c}{\displaystyle {\left(\frac{n_3}{n_2}\right)}^2+{\left(\frac{n_2}{n_1}\right)}^2=\text{sin}{}^2\alpha +\text{cos}{}^2\alpha =1.}\end{array}$

Rendezéssel: $n_1^2=n_2^2+n_3^2$, illetve $n_1=\sqrt[]{n_2^2+n_3^2}$. Ez $n_1$ azon értékét adja meg, amely mellett a fénysugár mindkét határfelületet a teljes visszaverődés feltételével érinti. Ha $n_1$ értéke nagyobb, a fénysugár behatolása a szálba és a szálban maradása még bizonyosabb. Tehát a válasz úgy szól, hogy $n_1$ törésmutatónak nem szabad kisebbnek lennie, mint a másik két törésmutató négyzetösszegének négyzetgyöke. Az eredmény $n_2$ és $n_3$ tekintetében szimmetrikus, e két anyag felcserélhető. Száloptikáról lévén szó, meg kell említeni, hogy az $n_3$-as közegből a szálba behatoló sugárnyaláb szálban maradása egyáltalán nem jelenti azt, hogy képalkotás is történik, vagyis, hogy a berendezés használható. Lényegében ugyanez a jelenség szerepel abban a közismert kísérletben, hogy egy üvegkocka oldaláról nem látható az üvegkocka alatt levő tárgy (az 1936. évi Eötvös verseny 3. feladata).
A feladatban kérdezett a) esetben $n_1=\sqrt[]{2}$, b) esetben $n_1=5/3$.

 

3. $48$ voltos generátor áramkörébe sorba kapcsolunk egy motort és egy kaloriméterbe helyezett $5$ ohm ellenállású vezetőt. A generátor és az egyéb kapcsoló huzalok ellenállása elhanyagolható. Ha a motor forgásban van, a kaloriméterben $72$ cal, ha pedig a motort akadályozzuk a forgásában, $1152\text{cal}$ hő keletkezik percenként. Mekkora forgás közben az indukált ellenelektromotoros erő és a motor kapocsfeszültsége?

 

Megoldás. Az áram hőhatásának $Q=0\mathrm{,}24I^{2}Rt$ törvénye alapján azonnal kiderül, hogy ha a motor áll ($Q=1152\text{cal}$, $R=5\text{ohm}$, $t=60\text{sec}$), az áramerősség 4 amper, ha a motor forog ($Q=72\text{cal}$, $R=5\text{ohm}$, $t=60\text{sec}$), az áramerősség 1 amper.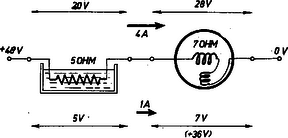

 

 

7. ábra

 

Először tárgyaljuk a forgásában megakadályozott motor esetét (7. ábra, a felső számok). Ha az áramerősség 4 amper, akkor a kaloriméterben levő 5 ohmra $4\cdot 5=20$ volt feszültségesés jut. Az áramforrás változatlan 48 voltos elektromotoros erejéből a motorra $48-20=28$ volt jut. Minthogy a motoron is átfolyik 4 amper, a motor tekercselésének ohmos ellenállása $28:4=7$ ohm értékű.
Most vizsgáljuk a forgásban levő motort (7. ábra, az alsó számok). 1 amperes áramerősség mellett a kaloriméterben levő 5 ohmra $1\cdot 5=5$ volt jut. A motortekercselések 7 ohmjára most $1\cdot 7=7$ voltnak kell jutnia. Marad az áramforrás 48 voltjából $48-5-7=36$ volt. Ekkora a forgáskor indukció által keltett ellenelektromotoros erő. A motor kivezetéseire eső kapocsfeszültség $36+7=43$ volt, vagy $48-5=43$ volt. Az ellenelektromotoros erővel szemben végzett munka alakul mechanikai munkává, így motorunk mechanikai teljesítménye $36\cdot 1=36$ watt, amely üresen járó motornál csapágysúrlódás, közegellenállás leküzdésére fordítódik. A motor által felvett teljesítmény $43\cdot 1=43$ watt, így a hatásfok $36/43=0\mathrm{,}84=84\%$.
Általánosságban és kaloriméter nélkül tárgyalva, ha a motor tekercselése $R$ ohm ellenállású, $U_0$ elektromotoros erejű feszültségforrásra van kapcsolva és állva $I_{\text{<span style="font-style: italic;">á</span>}}$, forogva $I_f$ az áramerősség, akkor a motor ohmos ellenállása $U_0/I_{\text{<span style="font-style: italic;">á</span>}}$ lévén a forgáskor ellenindukált elektromotoros erő

$\begin{array}{c}{\displaystyle U=U_0-I_f\cdot \frac{U_0}{I_{\text{<span style="font-style: italic;">á</span>}}}=U_0\left(1-\frac{I_f}{I_{\text{<span style="font-style: italic;">á</span>}}}\right)\mathrm{.}}\end{array}$