|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A fizikai kölcsönhatások gyakran kiegyenlítődő jellegűek: ha két vagy több test bizonyos tulajdonságai (sebesség, hőmérséklet) különböző értékűek, a kölcsönhatás során ezek kiegyenlítődnek, átlagolódnak. Másképpen fogalmazva azt is mondhatjuk, hogy több részből álló rendszer egy bizonyos sajátságát tekintve helyettesíthető eggyel. Ez utóbbi megfogalmazás általánosabb is, mert sztatikus esetekre, amikor keveredés nem történik, szintén alkalmazható.
Az átlagérték-képzés problémája már a változó mozgás tanulmányozásakor előkerült. Az átlagsebességet így definiáltuk: a megtett út osztva a megtételéhez szükséges idővel. Az átlagsebesség az az egyenletes sebesség, amellyel a mozgó test a meghatározott idő alatt ugyanakkora utat tesz meg, mint változó mozgása során. Tehát az átlagérték képzésekor a változónak egy olyan értékét keressük, amellyel az összes előforduló értéket helyettesítve valamely ‐ a szóban forgó értékektől függő mennyiség értéke ugyanaz marad. számú változó érték mellett az ún. számtani átlag az összefüggésből kapható: ahol a jel (szumma) összegezést jelent.
Az értékek között lehet több egyenlő is. Tegyük fel, hogy -szer fordul elő az összegben. Ezeket összevonva a következő összefüggést kapjuk: | |
azaz így ahol . (Az összegjel határait csak akkor írjuk ki, ha szükséges, egyébként értelemszerűen az összes összegzendőre vonatkozik.) Így jutunk el a súlyozott átlag fogalmához, megengedve, hogy a számok tetszőleges pozitív értéket vegyenek fel. Az értékek különböző erősséggel, súllyal szerepelnek az átlagban.
Az eddigiekben az átlagsebesség példájából kiindulva azt feltételeztük, hogy egy anyagi test valamilyen tulajdonsága vesz fel különböző értékeket. Átlagképzés viszont akkor is lehetséges, ha több test valamely közös tulajdonságának egy megfigyelés során felvett értékeiről van szó. Ilyen esetekben a súlyozás más jelentést is kaphat. Az átlagolásra kerülő egyedek az átlagképzés szempontjából különböző értékűek lehetnek.
Belátható, hogy a súlyozott átlag az átlagolandó sorozatban előforduló legnagyobb és legkisebb érték közé esik: Ennek bizonyítását az olvasóra bízzuk.
A továbbiakban vizsgáljuk meg, hol találkozunk súlyozott átlag képzésével a középiskolai fizika anyagban.
Rugalmatlan ütközés
Két test rugalmatlan ütközésekor a mozgásmennyiség nem változik meg: így a közös sebesség: Ütközés után mozgásukat együtt folytatják, sebességük a megfelelő tömegekkel súlyozva átlagolódik. Nyilvánvaló, hogy az összefüggés kettőnél több test rugalmatlan ütközése esetén is érvényes,
Fajsúlymérés
Ismeretes a már Archimedes által megoldott probléma: a szirakuzai király koronája aranytartalmának meghatározása. Az arany-ezüst korona súlya levegőben 20 egység, vízben egység, kérdés: mennyi a korona százalékos aranytartalma. Az adatokból a felhajtóerő egység. Jelöljük az arany súlyát -gyel, az ezüstét -vel, ekkor azaz ahol az ötvözet fajsúlyát jelenti, ebből Tehát a fajsúly átlagolódik a keveredés során, de az egyes anyagok fajsúlya a térfogattal súlyozva van.
A feladatban ismerjük értékét így, kiszámítható. térfogategység, hiszen a felhajtóerő egység és a víz fajsúlyát egységnyinek vesszük . Így
alapján | | (3.3) |
Ez az összefüggés az alkotórészek százalékos eloszlásának meghatározásához mindig felhasználható. Látható, hogy a fajsúlyátlag dimenziója csupán az általunk választott egységtől függ és független a súly és térfogat egységétől. A százalék pedig viszonyszám, amely dimenziómentes.
Párhuzamos erők összegezése
Egy testre (gerendára) ható erők összegezése, az eredő erő, illetve az egyensúlyhoz szükséges ellenerő támadáspontjának számítása is súlyozott átlagolásra vezet. Az egyensúly feltétele, hogy a testre ható erők és forgatónyomatékok összege nulla legyen: azaz
tehát
4.2-ből látható, hogy az egyensúlyozó, illetve az eredő erő karja a testre ható erők karjainak az erőkkel súlyozott átlaga.
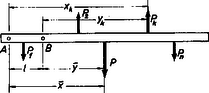 1. ábra
Könnyen beláthatjuk azt is, hogy a forgatónyomatékok felírásakor tetszőleges helyen vehetjük fel a vonatkoztatási pontot, akár a testen kívül is (1. ábra). Vegyük fel a vonatkoztatási pontot először -ban, majd -ben. A megfelelő erőkarokat jelöljük -szel, illetve -nal. Az ábrából látható, hogy Felírva az átlagképző egyenletet a 4.3 és 4.4 egyenletekből | | (4.5) |
4.5-ből kapjuk: | | (4.6) |
ami bizonyítja állításunkat, hogy az egyensúlyozó erő támadáspontja független a vonatkoztatási pont felvételétől.
Izotermikus gázok keveredése
Hasonlóan átlagolódnak a különböző térfogatban elhelyezkedő, különböző nyomású gázok nyomásértékei, ha állandó hőmérsékletet tartva, az elválasztófalakat kiemeljük. a kialakuló átlagnyomás az egyes nyomásoknak a megfelelő térfogatokkal súlyozott átlaga. Ezzel kapcsolatban még egy érdekességet említünk meg. Egy edényből álló rendszernél vizsgáljuk a -adik edényt, és tágítsuk ki az összes edény térfogatával egyenlő térfogatra. A Boyle-Mariotte törvény szerint a nyomás a egyenletből kapható. (A jobb megértés kedvéért két indexet használunk, de és egyaránt 1-től -ig fut.) 5.2-ből Ha ezt az eljárást minden edényre elvégezzük és összegezzük a -ket (most természetesen a index szerint), akkor | | (5.4) |
A kifejezés jobboldala egyenlő az 5.1 egyenlet jobboldalával. (Ne zavarjon az indexek különbözősége: helyébe ismét visszaírhatjuk az -t.) 5.1‐5.4-ből adódik az átlagnyomás az úgynevezett parciális nyomások összege.
Kalorimetria
Végül vizsgáljuk meg részletesebben a kalorimetriás jelenségeket. Két vagy több test közötti hőkicserélődés esetén alapfeltételünk, hogy hőmennyiség a rendszerből nem távozik el, és nem jut a rendszerbe. Két anyag keveredésekor az egyik által leadott hőt a másik felveszi: | | (6.1) |
innen | | (6.2) |
Látható, hogy a hőmérséklet az egyes hőmérsékleteknek a megfelelő értékekkel súlyozott átlaga. Ez érthető is, mert az -edik tömeg hőkapacitása. Tehát azokban az esetekben, ha átalakulási pontokon (olvadás, párolgás, stb.) nem megyünk keresztül, Az átalakulási pontokon áthaladó folyamatok esetében nehezebb a közös hőmérséklet meghatározása. Egy anyag különböző halmazállapotai esetében mégis találhatunk egy érdekes felírási módot.
Vezessük be az illető anyagra a hőmérsékleti skála helyett a következő hőskálát, amelyet a következőképpen definiálunk: szerint változik az átalakulási pontokon kívül, az egyes halmazállapotok között pedig az átalakulási hőnek megfelelő számértékű egység helyezkedik el. A jég-víz átalakulási pont környékén a függvény alakját a 2. ábra mutatja: és állandók értékét a skála nullpontjának tetszőleges megválasztásával adhatjuk meg.
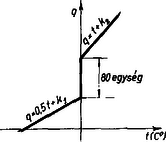 2. ábra
Egy számpéldán könnyebben megérthetjük ezt. Keverjünk össze kg -os jeget és kg -os vizet. Mi lesz belőle ?
Eddigi módszerünk szerint a vizet lehűtöttük -os jégé, és az így felszabadult hőmennyiséggel gazdálkodtunk az egész mennyiségre vonatkozóan. kg -os víz lehűtésekor hő szabadul fel, és van -os jegünk. Ha ezt a mennyiséget felmelegítjük -ra, akkor használódik fel. Marad még . A maradékból átalakul -os vízzé. és így víz.
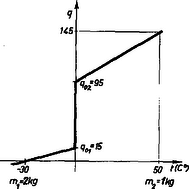 3. ábra
Tegyük át most a két tömeget a skála megfelelő pontjaira; legyen a jég a helyen. A skála most a 3. ábrán látható. Tehát -nál van tömeg, -nél tömeg. Átlagolunk -ra, súlyként a tömegeket választva: | | (6.4) |
Mit is tettünk ezzel tulajdonképpen ? A hőmérséklet átlagolása helyett az egységnyi tömegek hőtartalmát átlagoltuk a tömegekkel súlyozva. Matematikailag pedig a hőtartalom ‐ hőmérséklet összefüggés helyett, amelynek az átalakulási pontokon ugrása van, a folytonos függvényt vezettük be.
A 6.4 érték az átalakulási tartományban van. Képezzük a következő hányadost: | | (6.5) |
a vízzé alakult tömeg és az összes tömeg hányadosa: A pont ugyanis az átalakulási szakaszt a kétféle halmazállapot arányában osztja fel (a megfelelő szakaszok az ábrából láthatóan fordítva helyezkednek el). Ha egy halmazállapotnak megfelelő szakaszra kerül, akkor nem jelent nehézséget a megfelelő közös hőmérséklet megadása.
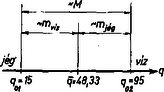 4. ábra
Különböző anyagok esetén, ha a folyamat során halmazállapot-változás is történik, az átlagoláskor nem használhatjuk ezt a módszert. Hőmérséklet-kiegyenlítődésnél még egy érdekes esetre hívjuk fel a figyelmet. Archimedes korona feladatánál az arány kiszámításához szükséges második egyenletet a felhajtóerő‐térfogat összefüggésből kapjuk. Előfordulhat azonban az is, hogy az ötvözet-arány megállapításához szükséges adatokat (a tömegmérésen kívül) kalorimetriás úton szerezzük meg.
Legyen egy két anyagból álló ötvözet tömege , hőmérséklete . Dobjuk az ötvözetet tömegű, hőmérsékletű folyadékba. A közös hőmérséklet . Ismerjük még a két anyag sűrűségét , fajhőjét és a hűtőfolyadék fajhőjét . Feladat: a tömegarányok és a közös sűrűség meghatározása.
A kalorimetriás adatokból: | | (6.7) |
ahol -sal az ötvözet fajhőjét jelöljük. | | (6.8) |
Hogyan jött létre ez a közös fajhő ? Nyilván összefüggésben van az ötvözetet alkotó anyagok hőkapacitásával. Ezeket szétválasztva a egyenletet írhatjuk fel, ahol , általános esetben Láthatjuk, hogy az ötvözet fajhője az összetevők fajhőinek a megfelelő tömegekkel súlyozott átlaga. Most ismét az a helyzet, hogy összeget ismerjük. 6.10 összefüggésben ezt felhasználva kapjuk, hogy | |
Rendezve A baloldalon ismert értékek, a jobboldalon az első összetevő tömegének az egész tömeghez viszonyított értéke áll. Az átlagsűrűséget 3.1-hez hasonlóan kapjuk: Most a tömegeket ismerjük (bár a térfogatokat is ki tudjuk számítani), ezért | |
A reciprok értéket véve Tehát a sűrűség reciprok értékei átlagolódnak, ha a térfogat helyett a tömeggel súlyozunk. Ez azonban már egy másfajta átlagképzés problémáihoz tartozik. |
 PDF | MathML
PDF | MathML 


