Cím:	A dinamikai példák megoldásáról
Szerző(k):	Major János
Füzet:	1965/február, 84 - 88. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A dinamikai példák megoldásáról   A mechanikai feladatok között sűrűn fordulnak elő a dinamikai (statikai és kinetikai) példák. Ezeket ‐ a Középiskolai Matematikai Lapok-hoz beérkező dolgozatok tanúsága szerint sokszor nem a legcélszerűbb módon szokták megoldani. Sokan a megoldásnak azt a módját választják, hogy egy erre az esetre alkalmazható ötletes gondolatmenetet felhasználva viszonylag kevés ,,írással'' röviden oldják meg a feladatot. A módszer hátránya, hogy csak az egyszerűbb feladatokra alkalmazható. Az általunk ajánlott módszerrel tetszőlegesen nehéz feladat megoldható néhány alapösszefüggés gépies alkalmazásával, és az esetleg felmerülő nehézségek csak matematikai természetűek lehetnek. A módszert példákon fogjuk bemutatni. Az első csoportba tartoznak a statikai feladatok: merev testek megadott rendszerében keressük a testek között ható erőket. Természetesen a rendszer paraméteresen is megadható, és a paraméter bizonyos értékeit keressük (ilyen lesz az első példa).   1. példa. Súrlódásmentes talajon vízszintes helyzetű hengert rögzítünk. Milyen maximális $\alpha$ szöget zárhat be az elég hosszú, nyugalomban levő deszka, ha a henger és a deszka közötti súrlódási együttható $\mu$ (l. az 1. ábrát)? Számítsuk ki a reakcióerőket is! 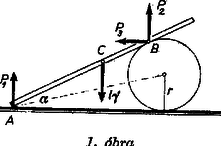    Megoldás. Legyen a deszka hossza $l$, súlya hosszegységenként $\gamma$, a henger sugara $r$. A deszka nyugalomban van, tehát a rá ható erők eredője nulla. Két helyen hat a deszkára reakcióerő: az $A$ és a $B$ pontban. Az $A$ pontban súrlódás nélkül érintkezik a talaj és a deszka vége, vagyis a köztük levő kölcsönhatás csak a talajra merőleges lehet. A deszkára itt a $P_1$ erő hat. A $B$ pontban nem ismerjük a kölcsönhatás irányát, ezért két egymásra merőleges $P_2$ és $P_3$ komponensét tekintjük ismeretlennek. A deszkára hat még a súlypontjában az $l\cdot \gamma$ nagyságú súlyerő. Azt, hogy ezen erők eredője nulla, csak vektoregyenlettel lehetne felírni, ehelyett inkább azt írjuk fel, hogy az erők vízszintes és függőleges komponenseinek eredője külön‐külön nulla: $\begin{array}{c}{\displaystyle P_1+P_2-l\cdot \gamma =0;P_3=0.}\end{array}$ Ez két egyenlet, de három ismeretlen van: $P_1$, $P_2$ és $P_3$. A hiányzó egyenlet felírásánál azt használjuk fel, hogy a deszkára ható erők forgatónyomatékainak összege bármely pontra nulla. A legegyszerűbb esetet keressük meg: az egyenletet a $B$ pontra írjuk fel, ugyanis erre a pontra a $P_2$ és $P_3$ erők nyomatéka nulla $$($\overline{AB}=r\cdot \text{ctg}\frac{\alpha }{2}$ és $\overline{BC}=r\cdot \text{ctg}\frac{\alpha }{2}-l/2$, az erők karja $\overline{AB}\cdot \text{cos}\alpha$ és $BC\cdot \text{cos}\alpha$$$): $\begin{array}{c}{\displaystyle l\cdot \gamma \left(r\cdot \text{ctg}\frac{\alpha }{2}-\frac{l}{2}\right)\cdot \text{cos}\alpha -P_1\cdot r\text{cos}\alpha \text{ctg}\frac{\alpha }{2}=0.}\end{array}$ Az $\alpha$ paraméter, egyelőre ismertnek tekintjük. Tehát megkaptuk a háromismeretlenes egyenletrendszert, melynek megoldása: $\begin{array}{c}{\displaystyle P_1=l\cdot \gamma \left(1-\frac{l}{2r}\text{ctg}\frac{a}{2}\right);P_2=\frac{l^2\gamma }{2r}\cdot \text{ctg}\frac{\alpha }{2};P_3=0.}\end{array}$ A súrlódás részletesebb megvizsgálásához számítsuk ki a $P_2$ erőnek az érintkező felületre merőleges és azokkal párhuzamos $P_N$ és $P_S$ komponensét: $P_N=P_2\cdot \text{cos}\alpha$ és $P_S=P_2\cdot \text{sin}\alpha$. Ha $P_S=\mu P_N$, vagyis $\mu =P_S/P_N=\text{tg}{\alpha }_0$, akkor éppen maximális szögben hajlik a deszka, hiszen ha $\alpha >{\alpha }_0$, akkor $P_S>\mu P_N$, ami lehetetlen ‐ a deszka lejjebb csúszik, viszont ha a $a\leqq a_0$, akkor $P_S\leqq \mu P_N$ ‐ a deszka nyugalomban marad. A megoldás során kihasználtuk azt, hogy a $C$ pont, a deszka súlypontja az $A$ és a $B$ pont között van, vagyis a deszka nem túl hosszú. Ha ez nem teljesül, akkor a maximális szöget akkor kapjuk, ha a $C$ pont egybeesik a $B$ ponttal, ugyanis ha a $B$ másik oldalára kerül, akkor a deszka átbillen. Ha $B$ és $C$ egybeesik, akkor $P_1=0$, $P_2=l\cdot \gamma$, $P_3=0$ és $\text{tg}\frac{\alpha }{2}=2r/l$ teljesül a maximális szögre. A megoldás menete tehát a következő: Az ábrán felrajzoljuk azokat az erőket, amelyek a testekre hatnak (tehát nem az ellenerejüket). Ezután felírjuk mindegyik testre, hogy a rájuk ható vízszintes és függőleges erők eredője nulla. Felírjuk minden egyes testre ‐ tetszőleges pontra ‐ a forgatónyomatékok egyensúlyát. Így annyi egyenletet kapunk, ahány ismeretlen van. (Ha kevesebbet kapnánk, akkor ez azt jelenti, hogy a feladat statikailag határozatlan.) A kapott egyenletrendszert megoldva nyerjük a keresett erőket, és ezzel a feladatot lényegében megoldottuk. Kövessük végig egy másik példa megoldásán ezt a módszert!     2. ábra     2. példa. A 2. ábrán látható elrendezésben a $G$ súlyú deszka súrlódásmentesen van megtámasztva két helyen, a felső végén a lecsúszás ellen kötéllel van rögzítve, és az alsó részére támaszkodó $Q$ súlyú és $r$ sugarú hengerre csavart fonál függőlegesen halad felfelé. A henger és a deszka közötti súrlódási együttható elég nagy ahhoz, hogy csúszás ne következzen be. Számítsuk ki a kötélerőket és a két támasznál levő reakcióerőt!   Megoldás. Rajzoljuk fel a deszkára ható erőket: a kötél húzza $P_1$ erővel, az első és a második támasz $P_2$ és $P_3$ erővel nyomja a felületre merőlegesen (súrlódás nincs), a súlyerő függőlegesen hat a súlypontban. A henger hatásának irányát nem ismerjük, ezért a $P_4$ és $P_6$ komponenseit rajzoljuk fel. A hengerre ható erők: a deszka hatása éppen ellentétes a hengernek a deszkára gyakorolt hatásával ($-P_4$ és $-P_5$), a súlyerő függőlegesen hat és a $P_6$ erő kötélirányú. Írjuk fel a deszkára ható erők vízszintes és függőleges komponenseinek összeget: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P_1}& {\displaystyle \cdot \text{cos}\alpha +P_2\cdot \text{sin}\alpha -P_3\text{sin}\alpha +P_4=0}\hfill \\ \hfill {\displaystyle -P_1}& {\displaystyle \cdot \text{sin}\alpha +P_2\cdot \text{cos}\alpha -P_3\cdot \text{cos}\alpha +G+P_5=0.}\hfill \end{array}}$ Hasonlóképpen a hengerre is felírjuk az erők egyensúlyát: $\begin{array}{c}{\displaystyle -P_5+Q-P_6=0;-P_4=0.}\end{array}$ Továbbá felírjuk azt, hogy a deszkára ható erők forgatónyomatékainak összege az $A$ pontra nulla: $\begin{array}{c}{\displaystyle -a\cdot P_2+b\cdot P_3-c\cdot G\cdot \text{cos}\alpha =0.}\end{array}$ Szintén az $A$ pontra felírjuk a hengerre ható erők nyomatékainak összégét: $\begin{array}{c}{\displaystyle Q\cdot r\cdot \text{sin}\alpha -P_6\cdot r\left(1+\text{sin}\alpha \right)=0.}\end{array}$ Így már megoldható az egyenletrendszer. A megoldás a következő: ${\displaystyle \begin{array}{c}\hfill {\displaystyle P_1=\frac{\text{sin}\alpha }{1+\text{sin}\alpha }\left[G\left(1+\text{sin}\alpha \right)+Q\right];P_2=\frac{\text{cos}\alpha }{1+\text{sin}\alpha }\cdot \frac{G\left(1+\text{sin}\alpha \right)\left(b-c\right)+bQ}{a-b};}\hfill \\ \hfill {\displaystyle P_3=\frac{\text{cos}\alpha }{1+sin\alpha }\cdot \frac{G\left(1+\text{sin}\alpha \right)\left(a-c\right)+a\cdot Q}{a-b};P_4=0;}\hfill \\ \hfill {\displaystyle P_5=Q\cdot \frac{1}{1+\text{sin}\alpha };P_6=\frac{\text{sin}\alpha }{1+\text{sin}\alpha }\mathrm{.}}\hfill \end{array}}$ A deszka és a henger közötti kölcsönhatás $P_4=0$ miatt függőleges irányú és $P_5$ nagyságú. Ezzel a feladatot megoldottuk ‐ a látszólag bonyolult példa megoldása során semmilyen nehézség nem lépett fel. A dinamikai feladatok másik csoportjába a kinetikai példák tartoznak. Ezeknél néhány merev test vagy tömegpont, a köztük levő kényszerek (kötél, lejtő stb.) és a rájuk ható erők (gravitációs, súrlódási erők stb.) adottak. Feladat a magára hagyott rendszer mozgásának leírása (általában elég a magára hagyott rendszer gyorsulását kiszámítani).   3. példa. $M$ tömegű, $2l$ hosszúságú hasáb közepén $m$ tömegű golyó nyugszik. A nulla időpillanattól kezdve $t$ ideig a hasábra állandó $P$ húzóerő hat. Ekkor az erőhatás megszűnik. Az alaplap és a hasáb közötti súrlódás elhanyagolható. A golyó és a hasáb közötti csúszó súrlódás biztosítja, hogy a golyó meg ne csússzék, hanem gördüljön. Mekkora $T$ idő múlva esik le a hasábról? (Mikor éri el a golyó a hasáb szélét?) A golyó gördülő ellenállása elhanyagolható. (Az 1963. évi középiskolai fizikai tanulmányi verseny II. fordulójának 3. feladata. Megoldással együtt megjelent a Középiskolai Matematikai Lapok 1963. évi 7. számában a 86. oldalon.)   Megoldás. Azt mindjárt látjuk, hogy a példa lényegileg megoldottnak tekinthető, ha az egyes gyorsulásokat és a golyó szöggyorsulását kiszámítjuk. Ennek érdekében írjuk fel mindkét testre a mozgásegyenletet! A hasáb gyorsulása legyen $A$, a golyóé $a$ ‐ külső koordinátarendszerből nézve. A golyó szöggyorsulása legyen $\beta$, valamint a golyó és a hasáb közötti kölcsönhatás legyen $K$ nagyságú erő. A hasábra ható erők éppen a gyorsítóerőt adják. Hat rá a $P$ erő és a golyó 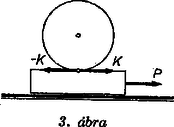$-K$ hatása: $MA=P-K$.     A golyóra csak a $K$ erő hat: $m\cdot a=K$. Most felírjuk a golyó forgásának egyenletét: a rá ható forgatónyomatékok összege egyenlő a tehetetlenségi nyomaték és a szöggyorsulás szorzatával: $\Theta \cdot \beta =K\cdot r$, ahol $\Theta =\frac{2}{5}m{r}^2$ a golyó tehetetlenségi nyomatéka és $r$ a golyó sugara. Ez eddig három egyenlet, és az ismeretlenek száma négy. A negyedik egyenletet a kényszerfeltétel adja meg (tehát az, hogy a golyó nem csúszhat a hasábon). Amíg a golyó $x$ utat tesz meg és $\alpha$ szöggel elfordul, addig a hasáb $X$ utat tesz meg, vagyis $a\cdot r+x=X$. Azonban $\alpha =\frac{1}{2}\beta \cdot t^2$, $x=\frac{1}{2}a\cdot t^2$ és $X=\frac{1}{2}A\cdot t^2$, tehát a negyedik egyenlet: $\beta r+a=A$.   Az egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle a=\frac{P}{M\left(\frac{7}{2}+\frac{m}{M}\right)};A=\frac{\frac{7}{2}P}{M\left(\frac{7}{2}+\frac{m}{M}\right)};\beta =\frac{\frac{5}{2}P}{M\left(\frac{7}{2}+\frac{m}{M}\right)}\mathrm{.}}\end{array}$ Ezen adatok ismeretében a kérdésre már könnyen válaszolhatunk. A megoldás menete tehát a következő: Minden gyorsuló mozgást végző testre felírjuk az $m\cdot a=\Sigma P$ mozgásegyenletet és minden forgó mozgást végző testre a $\Theta \beta =\Sigma M$ mozgásegyenletet. ($M$ itt forgatónyomatékot jelöl!): Az egyenletrendszer többi egyenletét a kényszerfeltételek megadásával kapjuk meg. Kissé bonyolultabb a helyzet akkor, ha a súrlódást nem hanyagolhatjuk el. Ha csúszó súrlódás van, akkor azt tudjuk, hogy a mozgás sebességével ellentétes irányú súrlódási erő $\mu N$, ahol $\mu$ a súrlódási együttható és $N$ a felületeket összenyomó erő. Ilyen feladatok esetén figyelembe kell venni a kezdeti feltételeket is, ugyanis a gyorsulás függ a sebesség irányától. (Például valamely lassuló mozgásnál a súrlódási erő a gyorsulás számértékét növeli, a megállás után, amikor a test már visszafelé mozog, a súrlódási erő irányt változtat és a gyorsulás számértékét csökkenti.) Ha tapadó súrlódás van, akkor a súrlódási erőnek nem ismerjük a nagyságát, csak azt tudjuk róla, hogy kisebb, mint $\mu N$. Ekkor azonban fel tudunk írni egy kényszeregyenletet a felületek tapadására (a 3. példában ez előfordult). Ha olyan példát kapunk, amelyben súrlódás is szerepel, rendszerint azzal a feltevéssel oldjuk meg, hogy kezdetben a rendszer nyugalomban volt. Ekkor először, hogy a súrlódási erők irányát megtudjuk, meghatározzuk a sebességek irányát (a sebesség irányával mindig ellentétes irányú a súrlódási erő). Ez úgy történik, hogy a súrlódás elhanyagolásával felírjuk a mozgásegyenleteket és a kényszeregyenleteket, és megoldjuk azokat. Ha a súrlódás már nem elhanyagolható, akkor legfeljebb csökken a mozgás gyorsulása, illetve sebessége, de az irányukon ez nem változtathat. Miután ismerjük a súrlódási erő irányát (és nagyságát is), felírjuk a végleges egyenletrendszert. Ha ennek megoldása az előző gyorsulással ellentétes irányú gyorsulást ad meg, akkor a helyes megoldás az, hogy a nagy súrlódás miatt a test nem indul meg. (Ha a súrlódási együtthatót növeljük, a lejtőn lecsúszó test nem indul el fölfelé, legfeljebb megáll.) Nézzük meg egy olyan példa megoldását, amelyben csúszó súrlódás szerepel! 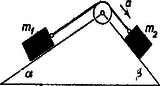    4. ábra   4. példa. A 4. ábrán látható összeállításban a súrlódási együttható $\mu =0\mathrm{,}1$, $m_1=10\text{kg}$, $m_2=15\text{kg}$, $\alpha ={30}^{\circ }$, $\beta ={45}^{\circ }$, a kötél ideális, igen jól csúszik a csigán. Számítsuk ki a $K$ kötélerőt és a gyorsulást!   Megoldás. Vegyük fel a gyorsulás irányát a nyíl szerint. A mozgásegyenletek a súrlódás figyelmen kívül hagyásával: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m_{1}a}& {\displaystyle =K-m_{1}g\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle m_{2}a}& {\displaystyle =-K+m_{2}g\text{sin}\beta \mathrm{.}}\hfill \end{array}}$ Az egyenletrendszer így megoldható, ugyanis a kényszerfeltételt akkor vettük figyelembe, amikor észrevettük, hogy mindkét test gyorsulása $a$. A megoldás: $a=g\cdot \frac{m_2\text{sin}\beta -m_1\text{sin}\alpha }{m_1+m_2}\approx 9\mathrm{,}81\cdot \frac{2\mathrm{,}12-1}{5}\frac{m}{{\text{sec}}^2}>0$, vagyis a pozitív irányt helyesen választottuk meg. Ezután már felírhatjuk a mozgásegyenleteket a súrlódás figyelembevételével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m_{1}a}& {\displaystyle =K-m_{1}g\text{sin}\alpha -\mu m_{1}g\text{cos}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle m_{2}a}& {\displaystyle =-K+m_{2}g\text{sin}\beta -\mu m_{2}g\text{cos}\beta \mathrm{.}}\hfill \end{array}}$ A megoldás: $a=12\mathrm{,}7{\text{ cm/sec}}^{-2}$, vagyis pozitív érték. Ha a súrlódási együttható pl. $0\mathrm{,}5$ lenne, akkor a gyorsulásra már negatív értéket kapnánk, a két test nem mozdulna meg. A következő feladatban tapadási súrlódás szerepel.   5. példa. $\alpha$ hajlásszögű lejtőn $m$ tömegű és $r$ sugarú homogén korong gurul le. A súrlódási együttható $\mu$. Mennyi lesz a korong gyorsulása?       Megoldás. A korongra az $mg\text{sin}\alpha$ és az $S$ súrlódási erő hat. Az $mg\text{cos}\alpha$ és a lejtő kényszerereje éppen kiegyenlítik egymást. A mozgásegyenletek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m\cdot a}& {\displaystyle =m\cdot g\text{sin}\alpha -S\mathrm{,}}\hfill \\ \hfill {\displaystyle \Theta \beta }& {\displaystyle =S\cdot r\mathrm{.}}\hfill \end{array}}$ A kényszerfeltétel a tapadás: $\beta \cdot r=a$. Az egyenletrendszer megoldása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a}& {\displaystyle =\frac{2}{3}g\cdot \text{sin}\alpha ;}\hfill \\ \hfill {\displaystyle S}& {\displaystyle =\frac{1}{3}mg\text{sin}\alpha ;}\hfill \\ \hfill {\displaystyle \beta }& {\displaystyle =\frac{2}{3}g\frac{\text{sin}\alpha }{r}\mathrm{.}}\hfill \end{array}}$ Ez azonban csak akkor igaz, ha $S⩽\mu \cdot mg\text{cos}\alpha$. Az $S>\mu mg\text{cos}\alpha$ már nem állhat fenn, ekkor $S=\mu \cdot mg\text{cos}\alpha$, és a korong csúszni fog. A mozgásegyenletek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m\cdot a}& {\displaystyle =m\cdot g\cdot \text{sin}\alpha -\mu mg\text{cos}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle \Theta \cdot \beta }& {\displaystyle =\mu \cdot mg\cdot r\cdot \text{cos}\alpha \mathrm{.}}\hfill \end{array}}$ A kényszerfeltételt nem írjuk fel, mert megszűnt a tapadás. Az eredmény: $\begin{array}{c}{\displaystyle a=g\left(\text{sin}\alpha -\mu \text{cos}\alpha \right);\beta =2\mu g\frac{\text{cos}\alpha }{r}\mathrm{.}}\end{array}$  Major János   (A szerző köszönetet mond Gaál István tud. kutatónak, aki az itt ismertetett eljárás lényeges gondolatait az Ifjúsági Fizikai Kör ülésein több előadásban kifejtette.)