Cím:	1964. évi Eötvös Loránd Fizikaverseny
Füzet:	1965/február, 81 - 83. oldal	PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1964. évi Eötvös Loránd fizikai verseny   Az Eötvös Loránd Fizikai Társulat október 3-án rendezte ez évi fizikai versenyét Budapesten és 6 vidéki városban az idén érettségizettek számára. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.   1. ${60}^{\circ }$-os és ${20}^{\circ }$-os hajlásszögű lejtők egy élben találkoznak. Itt kicsiny, súrlódásmentes csigát helyezünk el. A csigán átvetett fonál végein $m_1$ és $m_2$ tömegű ládák függnek, amelyek csúszó súrlódási együtthatója $0\mathrm{,}2$. Milyen feltétel mellett maradnak a ládák nyugalomban?   Megoldás. Az $m_1$ tömeg $m_{1}g$ súlyának lejtő menti összetevője $m_{1}g\text{sin}{\alpha }_2$, lejtőre merőleges összetevője $m_{1}g\text{cos}{\alpha }_2$. A keletkezhető legnagyobb súrlódási erő $\mu m_{1}g\text{cos}{\alpha }_2$, ha $\mu$-vel jelöljük a súrlódási együtthatót. Az $m_1$ tömegű láda leengedéskor $m_{1}g\text{sin}{\alpha }_2-\mu m_{1}g\text{cos}{\alpha }_2$ erővel tartható egyensúlyban, viszont felhúzásához legalább $m_{1}g\text{sin}{\alpha }_2+\mu m_{1}g\text{cos}{\alpha }_2$ erőt kell kifejtenünk (1. ábra). 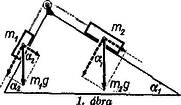    Hasonlóképp az $m_2$ tömegű láda lecsúszik, hacsak nem tartjuk a fonalat legalább $m_{2}g\text{sin}{\alpha }_1-\mu m_{2}g\text{cos}{\alpha }_1$ erővel és felfelé mozog, ha a jobboldali fonalat legalább $m_{2}g\text{sin}{\alpha }_1+\mu m_{2}g\text{cos}{\alpha }_1$ erővel húzzuk felfelé, minden esetben a lejtő hosszával párhuzamosan. A fonállal összekötött ládák nem csúsznak balfelé, ha $\begin{array}{c}{\displaystyle m_{1}g\text{sin}{\alpha }_2-\mu m_{1}g\text{cos}{\alpha }_2\leqq m_{2}g\text{sin}{\alpha }_1+\mu m_{2}g\text{cos}{\alpha }_1\mathrm{,}}\end{array}$ és nem csúsznak jobbfelé, ha $\begin{array}{c}{\displaystyle m_{2}g\text{sin}{\alpha }_1-\mu m_{2}g\text{cos}{\alpha }_1\leqq m_{1}g\text{sin}{\alpha }_2+\mu m_{1}g\text{cos}{\alpha }_2\mathrm{.}}\end{array}$ Az $m_1/m_2$ hányadost mindegyikből kifejezve, $g$-vel egyszerűsítve adódik a nyugalom feltétele: $\begin{array}{c}{\displaystyle \frac{\text{sin}{\alpha }_1-\mu \text{cos}{\alpha }_1}{\text{sin}{\alpha }_2+\mu \text{cos}{\alpha }_2}\leqq \frac{m_1}{m_2}\leqq \frac{\text{sin}{\alpha }_1+\mu \text{cos}{\alpha }_1}{\text{sin}{\alpha }_2-\mu \text{cos}{\alpha }_2}\mathrm{.}}\end{array}$ (1) Amennyiben a tömegviszony e két határ között van, a ládák nyugalomban maradnak. Felhasználhatjuk a súrlódási határszög fogalmát. E súrlódási határszög az a szög,amelynek tangense egyenlő a súrlódási együtthatóval: 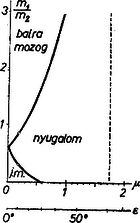$\begin{array}{c}{\displaystyle \text{tg}\epsilon =\mu =\frac{\text{sin}\epsilon }{\text{cos}\epsilon }\mathrm{.}}\end{array}$ Behelyettesítve (1)-be és bővítve cos $\epsilon$-nal: $\begin{array}{c}{\displaystyle \frac{\text{sin}{\alpha }_1\text{cos}\epsilon -\text{cos}{\alpha }_1\text{sin}\epsilon }{\text{sin}{\alpha }_2\text{cos}\epsilon +\text{cos}{\alpha }_2\text{sin}\epsilon }\leqq \frac{m_1}{m_2}\leqq \frac{\text{sin}{\alpha }_1\text{cos}\epsilon +\text{cos}{\alpha }_1\text{sin}\epsilon }{\text{sin}{\alpha }_2\text{cos}\epsilon -\text{cos}{\alpha }_2\text{sin}\epsilon }\mathrm{.}}\end{array}$ (2) Goniometriai átalakítással: $\begin{array}{c}{\displaystyle \frac{\text{sin}\left({\alpha }_1-\epsilon \right)}{\text{sin}\left({\alpha }_2+\epsilon \right)}\leqq \frac{m_1}{m_2}\leqq \frac{\text{sin}\left({\alpha }_1+\epsilon \right)}{\text{sin}\left({\alpha }_2-\epsilon \right)}\mathrm{.}}\end{array}$ Ez az egyenlőtlenség fejezi ki általában a nyugalom feltételét.     2. ábra   Ha mint feladatunkban is ${\alpha }_1+{\alpha }_2={90}^{\circ }$, akkor $\text{sin}{\alpha }_2$ helyébe $\text{cos}{\alpha }_1$ és $\text{cos}{\alpha }_2$ helyébe $\text{sin}{\alpha }_1$ tehető, és ezzel (2) így írható fel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\text{sin}{\alpha }_1\text{cos}\epsilon -\text{cos}{\alpha }_1\text{sin}\epsilon }{\text{cos}{\alpha }_1\text{cos}\epsilon +\text{sin}{\alpha }_1\text{sin}\epsilon }}& {\displaystyle \leqq \frac{m_1}{m_2}\leqq \frac{\text{sin}{\alpha }_1\text{cos}\epsilon +\text{cos}{\alpha }_1\text{sin}\epsilon }{\text{cos}{\alpha }_1\text{cos}\epsilon -\text{sin}{\alpha }_1\text{sin}\epsilon }\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}\left({\alpha }_1-\epsilon \right)}{\text{cos}\left({\alpha }_1-\epsilon \right)}}& {\displaystyle \leqq \frac{m_1}{m_2}\leqq \frac{\text{sin}\left({\alpha }_1+\epsilon \right)}{\text{cos}\left({\alpha }_1-\epsilon \right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{tg}\left({\alpha }_1-\epsilon \right)}& {\displaystyle \leqq \frac{m_1}{m_2}\leqq \text{tg}\left({\alpha }_1+\epsilon \right)\mathrm{.}}\hfill \end{array}}$ Ez az egyenlőtlenség fejezi ki legjobban az egyensúly feltételét feladatunk esetében. A feladat szövege szerint ${\alpha }_1={30}^{\circ }\mathrm{.}$ 2. ábránk az egyensúly két határa esetében érvényes tömegviszonyt ábrázolja e szögnél mint a $\mu$ súrlódási együttható függvényét. Ha a $\mu$ és $m_1/m_2$ tömegviszony által feltüntetett pont a felső görbe felett van, akkor a ládák balra mozognak, ha pedig az alsó görbe alatt, akkor jobbra. A két görbétől jobbra fekvő terület jelzi azon $m_1/m_2$ és $\mu$ értékpárokat, amelyek mellett nyugalom van. Ha ${\alpha }_1={30}^{\circ }$ és $\mu =0\mathrm{,}2$, akkor a nyugalom feltétele: $\begin{array}{c}{\displaystyle 0\mathrm{,}338\leqq \frac{m_1}{m_2}\leqq 0\mathrm{,}879.}\end{array}$ 2. Kilenc négyzetből álló hálózat mindegyik éle $R$ ohm ellenállású. A középső négyzetes mező helyébe tökéletesen vezető négyzetlapot teszünk. Mennyi az eredő ellenállás a négyzet két átellenes csúcsa között? (3. ábra) 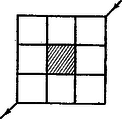 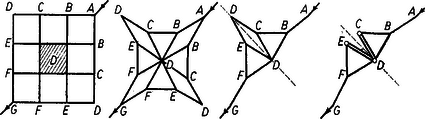   3. ábra     4. ábra   Megoldás. A tökéletesen vezető négyzetlaphoz csatlakozó ellenállások egyetlen $D$ pontban egyesíthetők (4. ábra első és második rajza). A vezetékhálózatot ferde átlójánál fogva kettévágjuk. Észrevesszük, hogy szimmetriaokokból a $D$ betűvel jelölt pontok közös potenciálon vannak (4. ábra harmadik és negyedik rajza); ezeket a pontokat egybeejtjük. A 4. ábra negyedik rajzán látható hálózat $AD$ részén először is $C$, $B$ között $R$ ohm és $C$, $D$ között $R/2$ ohm sorba van kapcsolva, ami $3R/2$ ohmot ad, azután ez a $D$, $B$ közötti $R$ ellenállással párhuzamosan van kapcsolva, így a $BD$ rész teljes ellenállása: $\begin{array}{c}{\displaystyle \frac{\frac{3R}{2}\cdot R}{\frac{3R}{2}+R}=\frac{3}{5}\cdot R\mathrm{.}}\end{array}$ Ehhez kapcsoljuk sorba az $A$, $B$ közötti $R$ ohmot, ami $3R/5+R=8R/5$ ohmot ad. $DG$ között ugyanennyi az ellenállás, viszont az ábrán látható hálózattal párhuzamosan van kapcsolva az átló alatt egy ugyanilyen alakzat, tehát az eredő ellenállás: $\begin{array}{c}{\displaystyle \frac{8}{5}\cdot R=1\mathrm{,}6R\mathrm{.}}\end{array}$ 3. Egy gyűjtőlencsét szemünkhöz közel helyezünk el úgy, hogy egy hengeres formájú parafadugó homlokfelületét a tisztán látás távolságában élesen látjuk. A dugó és lencse kölcsönös távolságát rögzítve elhelyezhetjük-e szemünket úgy, hogy a dugó palástfelületét is lássuk? A henger hossztengelye és a szem tengelye mindig a lencse tengelyében legyen.  (Pócza Jenő) 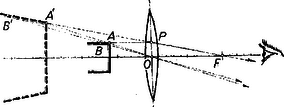    5. ábra   Megoldás. A feladat szövegéből következik, hogy a dugó homlokfelületének virtuális képét nézzük (5. ábra). A homlokfelület $A$ pontjának képét $AP$ tengellyel párhuzamos fénysugárral (amelynek folytatása $PF$ fókuszon átmenő sugár) és $AO$ középponton átmenő sugárral szerkesztjük meg. A virtuális kép $A\text{'}$-ben keletkezik. Keressük most a hengerpalást alkotójának $B$ pontjához tartozó képpontot. Az egyik szerkesztő sugár most is $AP$, a másik $BO$, és a kép helye a $B\text{'}$ pont. Látható, hogy a henger $AB$ alkotójának virtuális képe $A\text{'}B\text{'}$ egyenes, amelynek folytatása átmegy a lencse $F$ fókuszán. A lencsét úgy hagyják el a sugarak, mintha a dugó és lencse helyett az $A\text{'}B\text{'}$ alkotójú (világító) csonka kúp volna jelen, lencse nélkül. Rögtön nyilvánvaló: akkor látunk rá e csonka kúp palástjára, ha szemünket a gyújtóponton kívül helyezzük el. Tehát a feladat megoldása: szemünket a fókuszponton kívül kell elhelyezni. Természetesen szükséges feltétel még, hogy a lencse átmérője nagyobb legyen, mint a dugó alapkörének átmérője.   A verseny eredménye. I. díjat nyert Corradi Gábor (a győri benedekrendi gimnáziumban Grabner Oszvald tanítványa), II. díjat nyert Doskar Balázs (a budapesti Piarista Gimnáziumban Havas József, Szoboszlay András és Varga László tanítványa), III. díjat nyert Lakó Ferenc (a budapesti II. Rákóczi Ferenc gimnáziumban Kozma Péter tanítványa). Dicséretet kapott Petrányi Gyula (a debreceni gyakorló gimnáziumban Dr. Nagy László és Dr. Nagy Lászlóné tanítványa). A versenyen kívül részt vevő középiskolai tanulók közül dicséretet kaptak Pelikán József (a budapesti Fazekas gimnázium III. osztályában Wiedemann László és Szalay Béla tanítványa) és Antos György (a budapesti II. Rákóczi Ferenc gimnázium IV. osztályában Petyerity Géza tanítványa).