| Cím: | Az elektronoptika alapjai és néhány alkalmazása | ||
| Szerző(k): | Goda Gábor , Veszely Gyula | ||
| Füzet: | 1965/január, 33 - 45. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az elektronoptika alapjai és néhány alkalmazása Jelen cikkünkkel az a célunk, hogy a középiskolai elektromos és matematikai ismeretekkel rendelkezőknek az elektronoptikába vázlatos betekintést nyújtsunk, és néhány fontos műszaki alkalmazáson keresztül megvilágítsuk a terület jelentőségét. Ebből a célból először ismertetjük az elektronoptika alapjául szolgáló elektron‐ballisztikát, majd rátérünk a legfontosabb elektronoptikai készülékekre: a katódsugárcsőre, elektronmikroszkópra, ciklotronra, magnetronra. A következőkben az elektronok, protonok ‐ közös kifejezéssel a töltött részecskék ‐ mozgását csak vákuumban vizsgáljuk, és így a súrlódást teljesen elhanyagoljuk. Ezt megtehetjük, mert ‐ egyéb okokból is ‐ a készülékeinkben vákuum van. Továbbá a nehézségi erő hatását figyelmen kívül hagyjuk, mert az sokkal kisebb, mint az elektromos erőhatások. 1. Töltött részecske mozgása homogén elektrosztatikus térben Az elektronballisztika feladata, hogy megvizsgálja: milyen pályán és hogyan mozognak a töltött részecskék elektromos és mágneses terekben. Először a legegyszerűbb, de a gyakorlat számára igen fontos esetet tárgyaljuk. Csak elektromos térerősség legyen jelen és az is legyen homogén. Ilyet lehet megvalósítani például (jó közelítéssel) egy síkkondenzátor lemezei között. Tudjuk azt, hogy ha a síkkondenzátor lemezeire egyenfeszültséget kapcsolunk és a lemezek egymástól távolságra vannak, akkor a lemezek között kialakuló elektromos tér térerőssége:
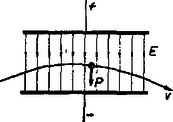 Töltött részecske pályája homogén villamos térben Lorentz szerint erősségű elektromos térben egy töltésű és tömegű részecskére
Minden mozgás vizsgálatához koordinátarendszer felvétele szükséges. Vegyük fel azért a koordinátarendszert, a részecske kezdősebességét és a térerő irányát a 2. ábrán látható módon. 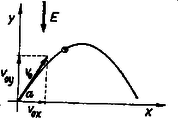 A pályaegyenlet meghatározása A mozgás pályáját Newton törvényéből kaphatjuk meg, amely szerint
Ha a (4) alatti úgynevezett mozgásegyenletet megoldjuk, azt kapjuk, hogy valamely idő alatt a részecske elmozdulása (komponenseként)
Ha a (7) kifejezésből felírjuk a pálya egyenletét, megkapjuk természetesen a 2. ábrán látható parabola egyenletét:
A fenti általános mozgás mellett nézzük meg a gyakorlatban igen fontos két speciális esetet. Először azt az esetet vizsgáljuk, amikor a részecske a koordinátarendszer kezdőpontjából nulla kezdősebességgel indul, tehát . Ilyenkor a mozgásegyenletek az alábbiak lesznek az (5), (8) és (7) egyenletekből: a gyorsulás
A második speciális esetben a részecske az elektromos erővonalakra merőlegesen lépjen be a térbe. Ilyenkor a 2. ábrából láthatóan amiből a pályaegyenlet
A pályaegyenletből látszik, hogy ez a mozgás a vízszintes hajlításnak felel meg. 2. A töltött részecske energiaviszonyai Kimutatható, hogy a sztatikus villamos és mágneses térben mozgó töltött részecske helyzeti energiája értékű, ahol a kérdéses pont potenciálja. Mivel a mozgási energiája , az energia‐egyensúly
Fejezzük ki a (17) egyenletből -t, azt kapjuk, hogy
Ez a képlet igen fontos gyakorlati összefüggés. Ennek segítségével ki lehet ugyanis számítani, hogy milyen sebességre gyorsítja fel a részecskét egy elektromos erőtér. Érdekes módon a részecske végsebessége csak a gyorsító feszültségtől függ, és attól nem, hogy milyen távolságot repül át. Nézzünk egy gyakorlati példát. Elektroncső anódjára a katódhoz képest 250 volt feszültséget kapcsolunk. Határozzuk meg, hogy milyen sebességgel csapódnak az elektronok az anódba? Mivel elektronra 3. Töltött részecske mozgása homogén mágneses térben Mágneses térben a töltött részecskére ható erő mindig merőleges a mágneses indukcióra () és merőleges a sebességre is. (Megjegyezzük, hogy a mágneses indukció és mágneses térerősség közötti kapcsolat: , ahol a permeabilitás.) Mivel az erő mindig merőleges a sebességre, a mágneses tér a sebességnek csak az irányát befolyásolja, a nagyságát nem. Ebből azonnal következik, hogy nyugvó részecskére mágneses térben nem hat erő, így az nyugalomban marad. Legyen először a kezdősebesség a 3. ábra szerint merőleges a mágneses térre. Ekkor a sebesség és az erő vektora is egy a -re merőleges síkban van, így a mozgás síkmozgás lesz, mégpedig olyan síkmozgás, melynél az erő a sebességre állandóan merőleges, és a sebesség abszolút értéke állandó. Ilyen síkmozgás egy van, az egyenletes körmozgás. A részecske tehát egy sugarú körpályán fog mozogni. 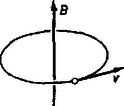 Töltött részecske mozgása homogén mágneses térben Lorentz szerint a mágneses térben a sebességgel mozgó részecskére ható erő nagysága
A körmozgás frekvenciája
A körpályán mozgó részecske energiája a (22) egyenlet alapján:
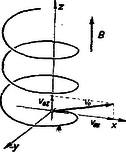 Töltött részecske mozgása homogén mágneses térben, általános irányú kezdősebesség esetén Ha a részecske sebessége úgy jött létre, hogy gyorsító feszültségen futott át, akkor a (19) összefüggés szerint
A fentiek arra az esetre vonatkoznak, amikor a kezdősebesség merőleges volt a mágneses térre. Ha a sebesség párhuzamos a -vel, a részecskére erő nem hat. Vizsgáljuk még meg röviden az általános esetet, amikor tehát a kezdősebesség vektora -vel tetszésszerinti szöget zár be. A viszonyokat a 4. ábrán látható térbeli koordinátarendszerben vizsgáljuk. Minden különösebb matematikai levezetés nélkül előre meg tudjuk mondani, hogy milyen lesz a mozgás pályája. A kezdősebességet felbontottuk és összetevőkre. A merőleges -re, így ez a sebességkomponens a fentiek alapján körmozgást eredményez. A viszont -vel nem ad erőt, mert egyirányúak, hanem csak egyenletes, egyenesvonalú mozgást jelent. Végeredményben egyenletes menetemelkedésű, körvetületű csavarmozgást kapunk. 4. Töltött részecske mozgása egyszerre ható villamos és mágneses térben Egyszerre ható villamos és mágneses tér esetén a két tér egymástól függetlenül hat, és a legkülönbözőbb mozgások léphetnek fel. Ezek közül mi csak néhány, a gyakorlat számára fontos esetet vizsgálunk meg. Először legyen az merőleges -re, és mindkettőre merőleges a részecske sebessége. Az 5. ábrán a pozitív kondenzátorlemeztől a negatív lemez felé mutat, pedig a papírra merőlegesen, az asztal felé. Ilyenkor a ,,nyilának'' a farkát látjuk, és ezt ábrázolja a kereszt. Ekkor a töltött részecskékre elektromos és mágneses erő is hat, amelyeknek értéke a (3) és a (20) egyenletek szerint 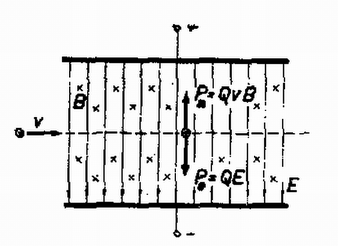 Töltött részecskére ható erő villamos és mágneses térben Az erők iránya ‐ amint az 5. ábrán látható ‐ egymással ellentétes, így előfordulhat, hogy a két erő egyenlő nagy, vagyis a mozgó részecskékre nem hat erő, irányváltozás nélkül elhagyja a lemezek terét. Ennek feltétele tehát:
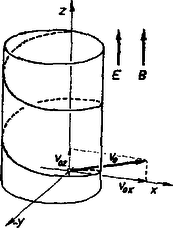 Töltött részecske mozgása párhuzamos elektromos és mágneses térben Bonyolultabb az eset akkor, ha a villamos és mágneses térerősség párhuzamos egymással, és a részecske kezdősebessége tetszőleges irányú (lásd a 6. ábrát). Ilyenkor a mágneses tér körmozgásra készteti a részecskét az , síkban (a hatására), az elektromos térerősség pedig a saját irányában, tehát a tengely mentén gyorsítja. A kettő eredményeképpen változó menetemelkedésű hengeres csavarvonalat kapunk. 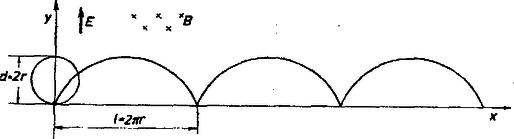 Töltött részecske mozgása egymásra merőleges villamos és mágneses térben, ha a kezdősebesség nulla Igen fontos a gyakorlati szempontból az az eset, amikor a villamos és mágneses tér merőleges egymásra, és a részecske nulla kezdősebességgel indul a koordinátarendszer kezdőpontjából (7. ábra). Amikor még a sebesség nulla, a mágneses tér nem gyakorol erőt a részecskére. Az elektromos tér azonban gyorsítani kezd a saját irányában, az -tengely felé. Ha azonban már van a részecskének sebessége, akkor a mágneses tér körpályájára próbálja kényszeríteni, és így ismét visszajutunk az -tengelybe. Ezzel a folyamatot elölről kezdjük. Ez a pálya ciklois pálya, mégpedig csúcsos ciklois, (egyenes mentén görbített kör egy kerületi pontja ír le ilyen görbét), ahol a gördülőkör sugara
Ha most ebben az elrendezésben nem nulla a kezdősebesség, hanem ; de az merőleges -re, akkor a csúcsos cikloisból hurkolt vagy nyújtott lesz (ilyen görbét írnak le a gördített körlemez belső, ill. külső pontjai), attól függően, hogy mekkora és milyen irányú ez a kezdősebesség. Ha a legáltalánosabb esetben a kezdősebesség nem is merőleges -re, akkor a ciklois pálya kiemelkedik az , síkból, és ferde ciklois pályán fog mozogni a részecske. 5. Töltött részecske mozgása igen erős terekben Az ,,igen erős tér'' most nem egy alig megvalósítható esetet jelent, hanem az atomfizikai részecskegyorsítókban nagyon sokszor ténylegesen fellépő alábbi jelenséget. Ha töltött részecske nagy potenciálkülönbséget fut át, akkor a (19) képlet szerint igen nagy sebességre gyorsul fel. Ekkor pedig a relativitáselmélet értelmében számolni kell azzal, hogy nagy sebességeknél a tömeg megnő az alábbi törvény szerint:
A fentieknek megfelelően elektronok esetében nagyon gyakran nem használhatjuk a (19) összefüggést, hanem a (30) alapján levezetett alábbi képlettel kell számolnunk:
A két képlet alkalmazhatóságáról annyit szükséges tudnunk, hogy ha a gyorsító feszültség 10 000 volt értékű, akkor már a (31) képlettel kell számolnunk, mert ha a (19) egyenlettel számolnánk, akkor körülbelül hibát követnénk el (elektron esetéit). 10 000 volt gyorsító feszültség felett feltétlenül a (31) egyenlettel számoljunk. A fentiekben elmondottak csak elektronra vonatkoznak, protonok és más nehéz részek gyorsításakor a gyakorlatban mindig elegendő pontosságot biztosít a (19) képlet is. 6. Elektrosztatikus eltérítésű katódsugárcső Az elektronoptika egyik legfontosabb alkalmazása a katódsugárcső eltérítő rendszere. Ennél a 8. ábra szerint egy izzószálból kilépő elektronok kondenzátorlemezek közé érkeznek. Erre a lemezpárra kapcsoljuk rá az eltérítő feszültséget, amelynek hatására az elektronok elhajlanak, ás az ernyőn távolsággal a középvonal felett csapódnak be, itt tehát világító pont jelenik meg. Határozzuk meg, hogy adott geometriai méretek és feszültségek esetén mekkora eltérítést kapunk az ernyőn. 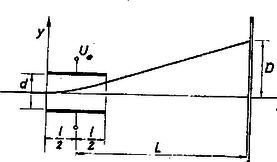 Elektrosztatikus eltérítésű katódsugárcső eltérítő rendszere Ez az eset, mivel mágneses tér nincs, és az elektronok -re merőlegesen lépnek be a térbe, az 1. fejezetben leírtaknak felel meg. A mozgásegyenletek tehát a (14), (15) és (16) egyenletek lesznek. A mozgás ‐ részletesebben megvizsgálva ‐ úgy alakul, hogy az elektronok sebességgel, egyenesvonalú egyenletes mozgással repülnek a tengelyben, egészen addig, amíg el nem érik a lemezek szélét. Ettől kezdve parabola alakú pályára kényszerülnek, majd a lemezek közül kilépve a pillanatnyi érintő irányában ugyancsak egyenesvonalú, egyenletes mozgással folytatják útjukat az ernyőig. A számítás kiindulási egyenlete tehát a (16) összefüggés:
A (32) összefüggésből látható, hogy az eltérítés annál nagyobb, minél nagyobb az eltérítő feszültség, és vele egyenesen arányos. Ezen a tényen alapszik a katódsugárcső felhasználása. Meg szokták adni az eltérítő rendszer érzékenységét, mely az egységnyi eltérítő feszültséghez tartozó eltérítés, azaz
Nézzünk a számadatok nagyságrendjének érzékeltetésére egy gyakorlati példát. Legyen az eltérítő lemezek hossza cm, távolságuk cm; az anódfeszültség volt, és az ernyő távolsága cm. Az eltérítő rendszer érzékenysége a (33) egyenletből: 7. Az optikai töréstörvény analógiája Az elektronoptika elnevezés egy érdekes analógiára utal, amely a következőképpen hangzik. Általános elektrosztatikus térben mozgó töltött részecske pályája megegyezik a térben meghatározott módon változó törésmutatóval bíró anyagban terjedő fénysugár útjával. A fénysugár útjára vonatkozó legfontosabb törvényszerűség a töréstörvény. Ezért a fenti analógia közelebbi vizsgálatához megnézzük, milyen törést szenved egy elektron pályája, amikor a részecske egy potenciálú térrészből egy potenciálú térrészbe halad át (9. ábra). 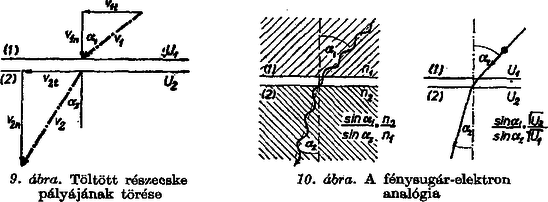 Az (1) és a (2) térrészben is a potenciál állandó, így a térerősség zérus, a két térrész között pedig a határfelületre merőleges. Ilymódon az elektron csak normális irányú gyorsulást szenved, tangenciális irányban a sebesség állandó marad: . Az ábrából: , és , ezért fenti egyenletünk így írható:
Használjuk most fel a (17) egyenletet meghatározására. (Az egyszerűség kedvéért feltételezzük, hogy az elektron zérus kezdősebességgel, nulla potenciálú helyről kerül az (1) térrészbe, azaz nulla energiával indult):
Összevetve ezt a Descartes‐Snellius-féle optikai töréstörvénnyel, látható, hogy az optikai törésmutatónak megfelelően bevezethetjük az elektromos törésmutatót, amely a potenciál négyzetgyökével arányos. Ezekután rajzoljuk meg a fejezet elején említett analógiát a 10. ábrán. Az analógiának igen nagy jelentősége van, hiszen az optikai készülékek elmélete jól kidolgozott, tulajdonságai szemléletesek. Ezeket átvihetjük az elektronok mozgására és az elektronikus készülékekre. Az analógia pl. elektronlencsék létezésére is figyelmeztet bennünket. 8. Elektromos lencsék Az elektronpálya töréstörvényének ismeretében az optikai lencse elektromos analogonját a 11. ábra szerint rajzolhatjuk meg. Az elektromos lencse fémhálóból készül (hogy az elektronok át tudjanak haladni rajta). A gyakorlatban azonban nem ez az elrendezés használatos. A gyakorlat elektromos lencséi olyan elektróda elrendezések, ahol az ekvipotenciális felületek megfelelnek a 11. ábra fémhálóinak. Például különböző potenciáira kapcsolt henger ekvipotenciális felületei kétszer domború lencsének felelnek meg (12. ábra). Itt persze a potenciál már nem ugrásszerűen, hanem folyamatosan változik. Ennek megfelelően az elektron pályája sem fog megtörni, hanem pontról‐pontra folyamatosan görbül. (Hasonlóképpen alakul a fénysugár útja olyan közegben, amelynek törésmutatója folytonosan változik.) Az optikai lencsékkel való hasonlóság kidomborítása végett a folytonosan változó potenciálú teret az ábrán vékony, ugrásszerűen változó potenciálú héjakra bontottuk. Készítenek elektromos lencsét két középen perforált lemezből is a 13. ábrán feltüntetett módon.  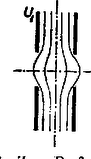 9. Mágneses lencsék A 3. fejezet szerint homogén mágneses térben tetszőleges irányú kezdősebesség esetén az elektron pályája körvetületű csavarvonal. Ha ezt a pályát a másik nézetből ábrázoljuk (14. ábra), látható, hogyan fokuszál a mágneses lencse: az egy pontból kiinduló, de irányra és nagyságra nézve különböző sebességű elektronokat ismét egy pontba gyűjti. (Ne felejtsük el, hogy a körülfordulás ideje [(23) szerint] nem függ a sebességtől. 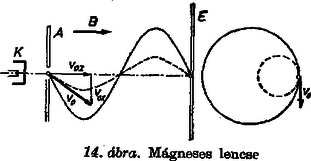 10. Az elektronmikroszkóp Akár elektromos, akár mágneses lencsékből felépíthető az elektronmikroszkóp. A 15. ábrán példaképpen elektrosztatikus elektronmikroszkópot vázoltunk. Itt az elektronforrás, , , gyorsító és egyben diafragmául szolgáló elektródák, a tárgylemez, és elektromos lencsék, a képlemez, amelyen a vizsgált tárgy képe megjelenik. 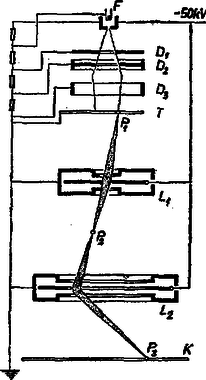 Elektrosztatikus elektronmikroszkóp vázlata Az elektronmikroszkóp nagy előnye az optikai mikroszkóppal szemben az, hogy felbontóképessége sokkal nagyobb. Így például optikai mikroszkóppal nagy nehézségek árán érhető el az, hogy két, egymástól 800 A távolságra levő pontot meg tudjunk különböztetni. Kiderül, hogy az elektronmikroszkópnál a felbontóképesség annál nagyobb, minél nagyobb az alkalmazott gyorsítófeszültség. A felbontóképesség növelésének elvileg csak a kvantummechanika határozatlansági relációja szab határt. Ebből ‐ a jelenleg alkalmazott elrendezéseknél 3 A adódik, mint a felbontóképesség korlátja. A mai elektronmikroszkópok megközelítik ezt a korlátot, felbontóképességük 10‐20 A. 11. A ciklotron Az atomfizikai kutatásokban nagyenergiájú részecskékre van szükség. Előállításukhoz alkalmas egyik legfontosabb eszköz a ciklotron. A ciklotron vázlatos felépítését a 16. ábra mutatja. A mágnes pólusai között két üres, nyílásukkal egymás felé fordított alakú fémdoboz helyezkedik el. A két fémdoboz közé váltakozó feszültséget kapcsolunk. 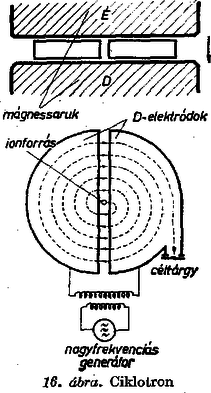 Működése a következő. Az elektródák közé helyezett ionforrásból kilépő ionok az elektromos tér hatására bejutnak valamely fémdoboz belsejébe, ahol elektromos tér gyakorlatilag nincs. De ekkor az ionok már bizonyos sebességgel bírnak, tehát a mágneses tér hatására körpályán fognak mozogni. Egy félkör befutása után a két elektróda közé kerülnek az ionok, így a villamos tér ismét hat rájuk, tehát sebességüket megnöveli, aminek következtében a másik elektróda belsejében már nagyobb sugarú körpályán fognak mozogni. (Lásd a 3. fejezet (22) képletét!) Eközben a villamos tér megfordul, így az elektródákból kilépő ionra ismét gyorsítólag hat. Ez a folyamat így folytatódik addig, míg a gyorsító méretei által megszabott legnagyobb sugáron a részecske el nem éri a maximális energiát. A működést az teszi lehetővé, hogy homogén mágneses térben a részecske körülfutási ideje nem függ sem a sebességtől, sem a sugártól, hiszen a 3.fejezet (23) képlete szerint . Tehát ha az elektromos tér frekvenciája , akkor biztosítva van, hogy a részecske a résbe érkezve mindig energiát nyerjen, azaz gyorsuljon. Határozzuk még meg a maximális energiát. (22)-ből a részecske legnagyobb sebessége: , ahol a lehetséges legnagyobb sugár, amelyet az elektródák mérete határoz meg. Ennek felhasználásával a maximális energia: 12. A magnetron Vizsgáljuk a 17. ábrán látható elrendezést (az úgynevezett síkmagnetront), amely tulajdonképpen egy síkkondenzátor, rá merőleges mágneses térben. 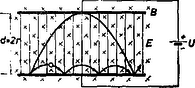 Síkmagnetron Az elektromos és mágneses tér tehát egymásra merőleges. Ha az egyik lemezből kezdősebesség nélküli elektronok lépnek ki, akkor azok a 4. fejezet 7. ábrája szerint ciklois pályán fognak mozogni, éspedig a (28) képlet szerint a gördülőkör sugara . Esetünkben ,
Ha a feszültség kicsi, akkor kicsi lesz a ciklois magassága (ami -rel egyenlő), így az elektronok nem érik el az anódlemezt, tehát anódáram nem fog folyni. A feszültséget növelve kapunk egy olyan ún. kritikus feszültséget, amelynél az anódáram éppen megindul. Ha viszont a feszültséget tartjuk állandó értéken, akkor az indukciót csökkenteni kell ahhoz, hogy az áram meginduljon, hiszen erősebb mágneses tér jobban meggörbíti az elektronok pályáját. Az áram megindulásának feltétele; , azaz A magnetronnak mint mikrohullámú elektroncsőnek a működése a fenti ciklois mozgáson alapul, ezzel azonban nem foglalkozunk. 13. Sebesség homogenizálás A 4. fejezet 5. ábráján látható elrendezés alkalmas arra, hogy a qtextitkülönböző sebességgel érkező részecskék közül (27) szerint csak a sebességűeket engedje tovább, mert a többinek a pályája elgörbül, és azok a lemezbe ütköznek. A fenti formula egyben meg is adja, hogy milyen sebességű részecskék jutnak ki a berendezésből. Gonda Gábor és Veszely Gyula |