Cím: Az 1965. évi Arany Dániel tanulóversenyek I. fordulóján kitűzött feladatok megoldása (kezdők versenye)
Szerző(k):  Scharnitzky Viktor 
Füzet: 1965/december, 193 - 196. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Legyen az ABC háromszög A csúcsából húzott magasság A1 talppontja a BC szakasz belső pontja. Mindig kisebb-e az AB és AC oldalak különbsége, mint az A1B és A1C szakaszok különbsége? (Indokolás)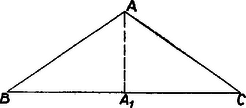

 
Megoldás. A feltett kérdésre a válasz tagadó. Ennek igazolására elég egyetlen olyan példát mutatni, amelyben az állítás nem teljesül. Az állítás egyenlő szárú háromszögben nem teljesül, ha a meghúzott magasság a háromszög szimmetriatengelye. Legyen ugyanis az ABC háromszögben (1. ábra) AB=AC, így a különbségük nulla, másrészt A1 felezi a BC alapot, tehát az A1B és A1C szakaszok különbsége is nulla. A szóban forgó két különbség tehát egyenlő.1
 
 

1. ábra
 

2. feladat. Oldjuk meg x-re a következő egyenletet:
1a+b+a+bx=1a-b+a-bx.(1)
Vizsgáljuk meg, hogy a és b milyen értékpárjainál hány megoldása van az egyenletnek.
 
I. megoldás. Az egyenletnek akkor van értelme, ha egyik tört nevezője sem nulla. Tegyük fel, hogy ez teljesül, azaz legyen a≠b, a≠-b, és x-nek csak a 0-tól különböző értékeit engedjük meg.
Gyűjtsük a bal oldalra az ismeretlent tartalmazó tagokat:
a+bx-a-bx=1a-b-1a+b,
majd hozzuk közös nevezőre a jobb oldalt is
2bx=2ba2-b2.(2)
A két egyenlő tört számlálója azonos. Ha ez nem nulla, akkor ebből következik, hogy a két nevező is egyenlő, vagyis
x=a2-b2.

Csak azonos átalakításokat végeztünk, a kapott érték valóban gyöke az egyenletnek, mert feltevésünk miatt x≠0, és így az egyenlet x-nevezőjű tagjainak is van értelme.
Ha b=0 (és így a feltevés szerint a≠0), akkor (2)-nek minden x≠0 szám eleget tesz, ugyanis (1) így alakul
1a+ax=1a+ax.(1a)

Ezek szerint a≠b≠0 és a≠-b esetén az egyenlet egyetlen megoldása x=a2-b2;
a≠b=0 esetén pedig minden szám megoldása az egyenletnek, kivéve x=0.
 

II. megoldás. Szorozzuk meg az egyenletet (a+b)(a-b)x-szel:
(a-b)x+(a+b)2(a-b)=(a+b)x+(a-b)2(a+b).
Tagokra bontás, rendezés majd kiemelés után
2b(x+b2-a2)=0.(3)
Ez akkor áll fenn, ha legalább az egyik tényező nulla. Ha b≠0, és a zárójelben levő kifejezés nulla, akkor
x=a2-b2,
és ezt (1) két oldalába külön-külön behelyettesítve az
1a+b+a+ba2-b2,illetve1a-b+a-ba2-b2
kifejezéseket kapjuk. Ha ennek a két kifejezésnek van értelme, azaz ha a≠b és a≠-b, akkor értékük egyenlő, vagyis x=a2-b2 gyöke az egyenletnek. Ha a=b vagy a=-b, akkor nincs megoldása az egyenletnek.
Ha b=0, akkor (3)-ban a és x bármely értéket felvehet, kivéve a nullát, mert ekkor ‐ mint (1a) mutatja ‐ az eredeti egyenletnek nincs értelme.
 

3. feladat. Fogadjuk el igaznak a következő állításokat:
(a) Vannak Beatles-frizurás huligánok.
(b) Minden huligánnak nyegle a modora.
Döntsük el és indokoljuk meg, hogy következnek-e ebből az alábbiak:
(c) Van olyan nyegle modorú huligán, akinek Beatles-frizurája van.
(d) Minden nyegle modorú huligánnak Beatles-frizurája van.
 

I. megoldás. A (c) állítás következik az (a) és (b) állításokból, mert (b) szerint minden huligánnak nyegle a modora, és így a Beatles-frizurás huligánok is nyegle modorúak ‐ ha vannak ‐, azonban (a) szerint vannak.
Így (c)-nél valamivel több következik (a)-ból és (b)-ből, ugyanis (c) csak azt állítja, hogy van nyegle modorú, Beatles-frizurájú huligán, mi pedig beláttuk, hogy többen is vannak ilyenek.
A (d) állítás viszont nem következik az igaznak elfogadott állításokból, mert attól, hogy minden huligán nyegle modorú ‐ amint (b) mondja ‐, és hogy így ‐ (a)-t is figyelembe véve ‐ vannak nyegle modorú, Beatles-frizurájú huligánok, még lehetnek olyan nyegle huligánok is, akiknek nincs Beatles-frizurájuk.
 

II. megoldás. Gondoljuk minden ember nevét egy-egy cédulára írva és e cédulákat egy E négyszög belsejében úgy elrendezve, hogy a nyegle modorúak, a huligánok, továbbá a Beatles-frizurások céduláit körülkeríthessük egy-egy N, H, ill. B vonallal. Ehhez N-nek ketté kell osztania E-t, H-nak N belsejét is, külsejét is, B-nek pedig az E tartomány így keletkezett mind a négy részét újra ketté kell vágnia (2. ábra). Miután egy-egy ember a mondott 3 tulajdonságból többel is rendelkezhet, a cédulákat a tartományokba úgy kell elhelyezni, hogy azoknak a tartományoknak a belsejében legyenek, amelyeknek megfelelő tulajdonsággal a név tulajdonosa rendelkezik, a többin pedig kívül.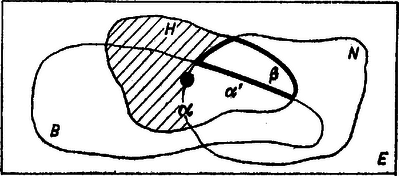

 
 

2. ábra
 

Az (a) állítás szerint a H és B görbék belsejének közös α részében vannak cédulák. Ezt a tényt egy a tartományba tett ponttal jelezzük. Mivel a tartományt N határa kettéosztja, és egyelőre nem tudjuk, hogy mindegyikbe jut-e cédula, és ha nem, melyikbe jut, így a pontot e határvonalra tettük. Viszont (b) szerint a H görbe belsejének az N-en kívüli része üres (az ábrán vonalkázva). Így az α részben levő cédulák csak a vonalkázatlan részben lehetnek, azaz N, H és B közös α' részében van cédula. Ez pedig éppen azt jelenti, amit (c) állít, tehát (c) következik az (a), (b) állítás-párból.
(d) azt jelentené, hogy N és H közös részének B-n kívüli β része üres lenne (vastag határvonal). Ez a rész nincs vonalkázva, tehát nem biztos, hogy üres, így (d) nem következik a feltételekből.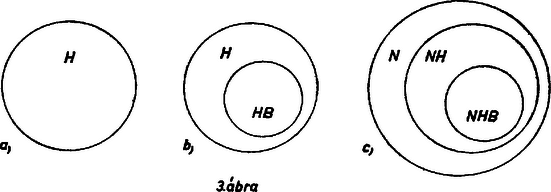
 
III. megoldás. Gyorsabban célhoz jutunk, ha az egyes tartományokat már az (a), (b) állítások figyelembevételével rajzoljuk meg. Képzeljünk minden huligánt a H görbe belsejébe (3/a ábra). Az (a) állítás szerint vannak Beatles-frizurájú huligánok, de nem biztos, hogy mind az: képzeljük a Beatles-frizurás huligánokat egy a H-ban levő HB görbe belsejébe (3/b ábra).
 
 
A (b) állítás szerint minden huligánnak nyegle a modora, viszont nem biztos, hogy minden nyegle modorú ember huligán, ezért a nyegle modorúak köré N görbét rajzolva ez a görbe magába zárja H-t (3/c ábra).
(c) következik (a)-ból és (b)-ből; mert az NHB görbébe képzelt emberek nyegle modorú Beatles-frizurás huligánok.
(d) nem következik a feltevésekből, mert H-nak a HB-n kívüli részében maradhattak huligánok, és ezek az NH-ban benne vannak, de az NHB-n kívül, tehát nyegle modorúak, de nincs Beatles-frizurájuk.
1A kérdés további vizsgálatára egy cikkben visszatérünk. ‐ Szerk.