| Cím: | Az 1965. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása | ||
| Szerző(k): | Scharnitzky Viktor | ||
| Füzet: | 1965/november, 97 - 104. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Oldjuk meg a következő egyenletrendszert: Megoldás. Adjuk hozzá az első egyenlethez a második egyenlet 3-szorosát, így a bal oldal lesz. Ebből köbgyökvonással
és akkor valósak, ha a négyzetgyök alatt pozitív szám vagy nulla áll. A négyzetgyök alatti tört értéke akkor pozitív, ha számlálója és nevezője egyszerre pozitív vagy negatív, tehát ha A négyzetgyök értéke nulla, ha (és , különben lenne), ekkor egy megoldás van: Ha végül , akkor , és ez a második egyenlettel csak úgy fér össze, ha ; ekkor is fennáll. Ekkor minden -re választással megoldását kapjuk az egyenletrendszernek. ‐ Ha viszont és , akkor az egyenletrendszernek nincs megoldása. 2. Az azonosság felhasználásával és a két egyenlet elosztásával az Numerikus adatok: , , , . A megoldások során a következő jelöléseket fogjuk használni: A járművek sebességét ‐ mint az ilyen feladatoknál ez szokásos ‐ állandónak tételezve fel, legyen a tehergépkocsi sebessége , a személygépkocsi sebessége , és távolsága , a hazaérkezés közös időpontja . A tehergépkocsi menetideje órával több, mint a személygépkocsié, mert az utóbbi -ból órával később indult, és -be órával később érkezett, mint a tehergépkocsi, azaz
esetén a gyök mindig valós. A negatív gyöknek nem tulajdonítunk értelmet. A második találkozás után mind a két gépkocsi még ideig volt úton, és ezalatt együttesen ismét befutották az utat, azaz A numerikus adatokkal 2. Hasonló gondolatmenettel is meghatározható. A visszaindulástól a második találkozásig a tehergépkocsi a személygépkocsi előtt álló utat tette meg. Ehhez időre volt szüksége. Hasonlóan a személygépkocsi a találkozás előtt idővel indult vissza. Ennek a két időnek a különbsége egyben az egész út megtételéhez szükséges idők különbsége is. Az odamenetre vonatkozó adatok szerint ez az időkülönbség , azaz Most már kiszámíthatjuk a második találkozástól a hazaérkezésig eltelt időt. Ennyi idő alatt a teherautó az egész út részét, a személyautó az részét teszi meg, a kettő együtt az egész utat ‐ az út 1-szeresét ‐ adja, azaz A numerikus adatokkal , adódik. Mindegyik autó oda-vissza útját (külön-külön) egyenlő hajlású szakaszok ábrázolják, ezért végpontjaik, valamint a találkozásokat jelentő pontok közül alkalmasan választott ponthármasok hasonló háromszögeket határoznak meg, és ezek alapjából a találkozási pontok vetületei arányos részeket vágnak le. Az 1. ábra jelöléseivel 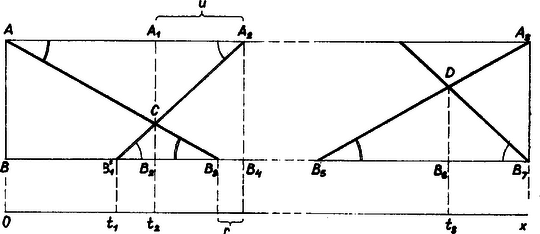 1. ábra Numerikusan óra, és óra. 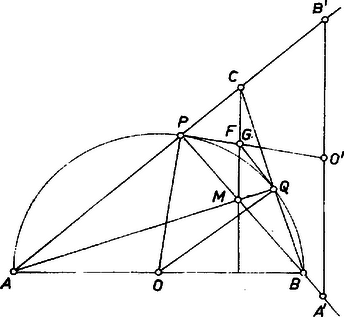 I. megoldás. Messe a magasságvonalat a kör -beli érintője -ben, a -beli érintő -ben (2. ábra). Azt kell belátnunk, hogy és egybeesnek. Thalész tétele miatt a -ből húzott magasság talppontja, ezért a körüli, pozitív irányú -os elforgatás az háromszöget átviszi egy a hozzá hasonló háromszöggel párhuzamos oldalú háromszögbe, a sugarat pedig a rá merőleges érintőre. Mivel felezi -t, azért a szakasz felezőpontja. Az háromszöget körül az előbbivel ellentétes irányban átforgatva a háromszöggel hasonló helyzetbe, ugyanígy látható, hogy is a szakasz felezőpontja, azaz egybeesik -fel. ‐ Ezzel a feladat állításánál többet bizonyítottunk be, mégpedig azt, hogy a kérdéses metszéspont felezi a magasságpont és az első oldallal szemben fekvő csúcs közti szakaszt. A háromszög egyenlő szárú; -nél és -nál levő szöge egyenlő a kör ívéhez tartozó bármely kerületi szöggel, így a szöggel is, melynek nagysága a derékszögű háromszögből . Ezért a szakasz -ból szögben látszik. -nak -ből vett látószöge viszont , és mivel és a egyenesnek ugyanazon a partján van, azért a körül írt, -n és -n átmenő kör átmegy a csúcson is. Ezért a háromszög egyenlő szárú, tehát
A szög csúcsszöge egy a íven nyugvó kerületi szög, ezért egyenlő az ugyanazon az íven nyugvó szöggel, ami . Így a háromszög -nél levő szöge , vagyis a -nél levő szögének pótszöge, ezért a -nél levő szöge derékszög, vagyis valóban merőleges -re. 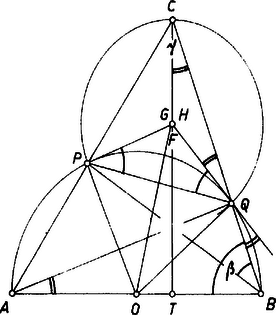 III. megoldás. A -ből húzott magasság és a pontbeli érintő metszéspontját ismét -vel jelölve azt fogjuk megmutatni, hogy a mint középpont körül írt, -n áthaladó körön rajta van is, is (3. ábra). Ebből ugyanis már következik, hogy , és így az és háromszögek három-három oldalban megegyezve egybevágóak, ezért a szög egyenlő a szöggel, az utóbbi pedig , tehát a -ben húzott körérintő. Az és háromszögek oldalai páronként merőlegesek egymásra, tehát a háromszögek hasonlóak, és így az előbbivel együtt az utóbbi is egyenlő szárú háromszög, , valóban a mondott körön van, és Másrészt az húrnégyszögben az belső és a külső szög egyenlő, mert mindkettő az szög -ra kiegészítő szöge, ezért 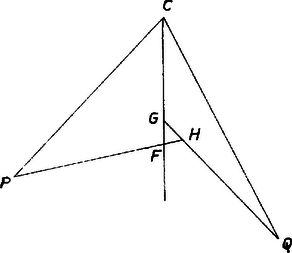 Ha , és nem esne egybe, és például a szakasz belső pontja lenne (4. ábra), akkor a szakasz -en túli meghosszabbításán és a szakasz belsejében lenne, mert így (és az eredeti feltevések szerint) belső pontban metszi a háromszög oldalát, a oldalát viszont a meghosszabbításán, tehát a oldalt is belső pontban metszi, vagyis Ha esnék a szakaszra, akkor hasonlóan adódik, hogy mindenütt az ellenkező értelmű egyenlőtlenség állana fenn, ami ugyancsak lehetetlen. Kell tehát, hogy a három pont egybeessék, és így az érintők a magasságvonalon messék egymást.  V. megoldás. Legyen a két érintő metszéspontja , a csúcsból húzott magasság talppontja (5. ábra). Említettük már, hogy és a háromszög másik két magassága. és háromszögek derékszögűek, és az szakasz mint átmérő fölé rajzolt kör átmegy -n és -n. Megmutatjuk. hogy ez a kör átmegy a talpponton is1. Ebből már következik a feladat állítása, ugyanis ekkor az derékszög szára átmegy az -ból induló átmérő másik végpontján, a ponton is. Az és a szög, mint a , illetőleg egyenlő szárú háromszög külső szöge, , illetve nagyságú, másrészt együttesen a -ot egyszer és a szöget kétszeresen fedik le, így Az és négyszögek húrnégyszögek (az első az , a második a mint átmérő fölé rajzolt Thalesz-körben), és így a , illetőleg külső szögük egyenlő a szöggel. Ezek alapján Mivel és a egyenesnek ugyanazon az oldalán fekszik, azért , , és valóban egy körön van, és ezzel igazoltuk állításunkat. 2. Ha az háromszög bármelyik szöge derékszög, a feladat állítása érdektelen. Ha ugyanis a derékszög -nél van, a kérdéses érintők, ha pedig és valamelyikénél van, akkor az egyik érintő és a magasság esik egybe. 3. Az olvasó a fenti megoldások csekély változtatásával könnyen beláthatja, hogy az állítás tompaszögű háromszögre is igaz, oldalszakasz helyett természetesen oldalegyenest mondva. Egy ilyen helyzetet mutat be a 6. ábra. 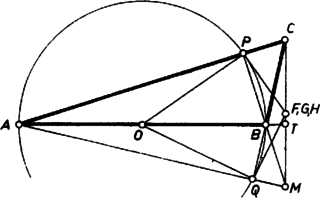 Scharnitzky Viktor 1A kör az háromszög Feuerbach-köre, amely átmegy a magasságok talppontjain, az oldalak felezőpontjain és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjain. Lásd pl. Gallai T.‐ Hódi E. ‐ Péter R. ‐ Szabó P. ‐ Tolnai J.: Matematika az ált. gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Bp. 1962. 183 ‐ 188. o. ‐ Az alábbiakban azonban erre való hivatkozás nélkül bizonyítjuk be állításunkat. |