Cím: Az 1964. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, haladók versenye
Szerző(k):  Lőrincz Pál ,  Surányi János 
Füzet: 1965/február, 49 - 56. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A) Az általános verseny feladatai:

 

1. feladat. Egy hatjegyű négyzetszámot három kétjegyű számra vágunk szét. A két szélső egyenlő, a középső pedig a fele ezek egyikének. Melyik e hatjegyű négyzetszám?
 

Megoldás. Legyen a kérdéses négyzetszám n2 és jelöljük a középső két jegyéből alkotott számot x-szel. Így a két szélső kétjegyű szám 2x, ezért
10≦2x<100,
és így
5≦x<50,(1)
másrészt
n2=2x⋅104+x⋅102+2x=20102x=2⋅19⋅232⋅x.

Egy négyzetszámot különböző törzsszámok hatványainak szorzataként előállítva minden kitevő páros. Ezért x ilyen előállításában a 2 és 19 törzsszámok páratlan kitevővel szerepelnek, s így a kitevőjük legalább 1, viszont minden más törzsszámhatványban páros szám a kitevő. Eszerint 2 és 19 első hatványát különválasztva, a többieket pedig összefoglalva x így írható:
x=2⋅19⋅k2=38k2,és ígyn2=(2⋅19⋅23⋅k)2,
ahol k egész szám. (1) csak k=1 esetén teljesül, így az egyetlen lehetséges megoldás:
n2=(2⋅19⋅23)2=8742=763876.

Ez valóban meg is felel a feladat követelményeinek.
 

2. feladat. Oldjuk meg a következő egyenletet:
x+x-x-x=32xx+x.(2)

Megoldás. Ahhoz, hogy az egyenletben szereplő kifejezéseknek értelme legyen, kell, hogy x>0, továbbá x-x≧0 legyen. Az utóbbi pozitív x-re akkor és csak akkor teljesül, ha
x≧1.(3)
Ilyen x-ekre a jobb oldali négyzetgyökös kifejezéssel végig oszthatjuk (2)-t, az egyenlet 1-nél nem kisebb x-ekre akkor és csak akkor teljesül, ha
x+xx+x2-xx=x+1-x-1=32,
azaz ha
x-12=x-1.(4)

Itt a bal oldal a (3) feltétel mellett pozitív, tehát a két oldal (a gyököket nem negatívnak véve) akkor és csak akkor egyenlő, ha a négyzeteik egyenlők:
x-x+14=x-1,x=54,x=2516.
Ez 1-nél nagyobb szám, tehát az egyenlet egyetlen megoldása.
 

Megjegyzés: (4)-et x-x-1=1/2 alakban írva, majd a pozitív 2(x+x-1) kifejezéssel szorozva a x+x-1=2 egyenlet adódik, amiből és az előbbiből, mint elsőfokú egyenletrendszerből ismét x=5/4 és az ezzel összhangban levő x-1=3/4 eredmény adódik.
 

3. feladat. Az ABCD paralelogramma A csúcsán átmenő kör az AB és az AD oldal egyenesét az F, illetőleg a H pontban, az AC átló egyenesét pedig a G pontban metszi. Bizonyítsuk be, hogy
AB⋅AF+AD⋅AH=AC⋅AG.(5)

Megoldás. Legyen F tükörképe AG felező merőlegesére F', az AG és F'H egyenesek metszéspontja M.
I. Vizsgáljuk először azt az esetet, amikor F, G, H sorra az A-ból B, C, D felé induló félegyenesen van. Ekkor az AC egyenes elválasztja a B és D pontokat és velük együtt az F és H pontokat is. Így az AC egyenes A és G pontjaival kettévágott körnek különböző ívein van F és H, F' pedig ugyanazon az íven van, mint F, mert FF'∥AG. Ebből következik, hogy M az AG húr belső pontja.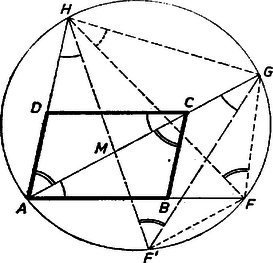
 
 
1. ábra
 

Megmutatjuk, hogy az
AHM,ACD,F'GMésCAB(6)
háromszögek hasonlók, megfelelő szögeik egyenlők. Ebből már könnyen fog következni (6). A háromszögek megfelelő szögeire egyrészt

ACB∢̲=CAD∢̲=HAM∢̲=HAG∢=HF'G∢=MF'G∢̲;
az utolsó előtti és az azt megelőző szög azonos íven nyugvó kerületi szögek. Másrészt
AHM∢̲=AHF'∢=AGF'∢=MGF'∢̲=FAG∢=CAB∢̲=ACD∢̲.


A második és harmadik szög azonos íven nyugvó kerületi szögek, a negyedik és ötödik pedig egymás tükörképe. A (6) alatti első és második háromszög hasonlóságából, illetőleg a harmadik és negyedik hasonlóságából a következő arányok egyenlősége olvasható le:
AHAM=ACAD,GF'GM=ACAB.
Innen, figyelembe véve, hogy GF' és AF egymás tükörképei, tehát egyenlők, kapjuk, hogy
AD⋅AH=AC⋅AM,AB⋅AF=AC⋅GM,
és a kettőt összeadva, mivel AM+MG=AG, adódik az (5) egyenlőség.
II. Megmutatjuk, hogy az (5) egyenlőség a kör minden helyzeténél érvényes marad, ha az A-tól B-vel, C-vel, ill. D-vel ellentétes irányban levő pontok távolságát negatívnak tekintjük. Ennek belátására forgassuk a kört az A pont körül pl. az óramutató járásával ellentétes irányban. A fenti bizonyítás nem alkalmazható már, ha a kör az AB oldalt érintő helyzetbe kerül (2. ábra). Ekkor AF=0, másrészt az ACD és AHG háromszögek hasonlók, mert egy szögük közös és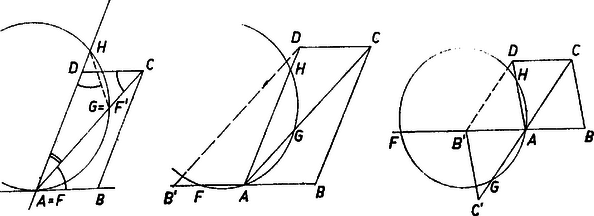
ACD∢=CAB∢=GAB∢=GHA∢.
Az utolsó egyenlőségben azonos íven nyugvó kerületi szögek szerepelnek. Így
ACAD=AHAG,AC⋅AG=AD⋅AH=AB⋅AF+AD⋅AH.

 
 
2.,  3.   és   4. ábra
 

Ha a kör továbbfordul, F az AB oldal A-n túli meghosszabbítására kerül (G és H még az AC és AD félegyeneseken lesz, 3. ábra). Jelöljük B-nek A-ra vonatkozó tükörképét B'-vel, ekkor az ACDB' paralelogrammára érvényes az I. alatti bizonyítás és azt adja, hogy
AC⋅AG+AB'⋅AF=AD⋅AH,
azaz
AC⋅AG=AB'⋅(-AF)+AD⋅AH.
Így ha magán az AF jelölésen a szakasz negatív előjellel vett hosszát értjük ebben az esetben, akkor az eredeti összefüggés változatlanul helyes marad.
Ha a kör továbbfordulásával G is az AC átló A-n túli meghosszabbítására kerül, akkor vegyük a B és C pontok A-ra vonatkozó B' és C' tükörképét. Az ADB'C' paralelogrammára ismét alkalmazható az I. rész bizonyítása, s így (4. ábra)
AC'⋅AG+AD⋅AH=AB'⋅AF,
azaz
AB⋅(-AF)+AD⋅AH=AC⋅(-AG).
Ez azonban ismét azt jelenti, hogy a II. elején mondott előjelmegállapodással (5) érvényben marad.
Ha a kör az AD-t A-ban érintő helyzeten is túlfordul, akkor korábban már tekintetbe vett körhelyzetek A-ra vonatkozó tükörképeit kapjuk. Egy ilyen tükrözés előjelmegállapodásunk szerint AF, AG és AH előjelének egyidejű megváltozását, és így (5) minden tagjának ellenkező előjelűre változását okozza, az egyenlőség helyességét tehát nem változtatja meg. Ezzel a II. alatti állítást is igazoltuk.
 

Megjegyzések. 1. Könnyen látható (1. ábra), hogy ABC▵∼FGH▵. A megfelelő szakaszok arányát h-val jelölve AB=h⋅GH, AC=h⋅FH, BC=AD=h⋅FG. Ezeket (5)-be beírva és h-val egyszerűsítve az AFGH húrnégyszögre a következő összefüggést kapjuk:
AF⋅GH+FG⋅HA=AG⋅FH,
vagyis húrnégyszögben a szemközti oldalpárok szorzatainak az összege az átlók szorzatával egyenlő. Ez az összefüggés PTOLEMAIOS tétele néven ismeretes. A fenti hasonlóság felhasználásával természetesen ebből a feladat állítása is könnyen következik. Ha viszont az I. alatti bizonyításban az ACD és CAB háromszög helyébe egyaránt az FHG háromszöget tesszük, akkor közvetlen bizonyítást kapunk PTOLEMAIOS tételére.
 

2. A versenyen a bíráló bizottság megelégedett az I. eset tárgyalásával.
 

B) A speciális matematikai osztály versenyének feladatai:
 

1. feladat. Egy hatjegyű négyzetszámot három kétjegyű számra vágunk szét. E három kétjegyű szám közül a középső egyenlő az előtte állóval, az utolsó és a középső kétjegyű szám különbsége négyzetszám. Melyik az eredeti hatjegyű szám?
 

Megoldás. Jelöljük a hatjegyű négyzetszámot n2-tel, ennek középső részét alkotó kétjegyű számot x-szel, az utolsó és a középső kétjegyű szám különbségét y2-tel. Ekkor feladatunk követelménye így írható:
n2=x⋅104+x⋅102+(x+y2)=10101x+y2.
Ezt átrendezéssel és az együtthatót törzsszámok szorzatára bontva a következő alakra hozhatjuk:
(n+y)(n-y)=37⋅13⋅7⋅3⋅x.(7)

n2 hatjegyű, ez azt jelenti, hogy 105≦n2<106. Mivel 3162<105<3172, így
317≦n≦999.

Másrészt x és x+y2 kétjegyű számok:
x≧10  és  x+y2≤99,(8)
így
y2≦99-x≦99-10=89;
és mivel nyilván elegendő y nem negatív értékeire szorítkoznunk, azért 0≦y≦9.
Így (7) bal oldalának tényezőire a következő korlátozások állnak fenn:
{n+y≦999+9=1008,(9)n-y≧317-9=1308,
továbbá a két tényező különbségére:
(n+y)-(n-y)=2y≦18.(10)
Ezek szerint olyan x kétjegyű számot kell keresnünk, hogy (7) jobb oldala a (9)‐(10) korlátozásoknak megfelelő két egész tényező szorzatára legyen bontható, belőlük n és y is egésznek adódjék, végül x-re és y-ra (8) is teljesüljön. Evégett minden szóba jövő módon két tényezős szorzattá próbáljuk alakítani (7) jobb oldalát, gondolva x felbontására is, legyen x=x1x2 (x1 és x2 egyike lehet 1 is).
A (7) alatti törzsszámok szorzata nagyobb 1008-nál, így nem lehet mind ugyanabban a tényezőben. Két 1008-nál kisebb tényezőre a következő módokon bontható szét:
13⋅777,21⋅481,37⋅273,39⋅259és91⋅111.

(7) bal oldalának két tényezőjét 13x1 és 777x2 alakban keresve (9) miatt csak x2=1 felel meg, ez a tényező 777, ennélfogva (10) miatt a másik tényezőre
777-18=759≦13x1≦795=777+18,
amiből, 13-mal osztva, és a hányadosnak csak az egész részét kiírva
58<x1≦61.
n és y csak akkor egész, ha összegük és különbségük ugyanolyan párosságú. A 777-es tényező páratlan, ezért csak x'1=59 és x''1=61 jön szóba.
Az első esetben x=x'1x2=59, a második tényező 13⋅59=767, kisebb 777-nél, így n+y=777, n-y=767; amiből n=772, y=5; és x+y2=84, kétjegyű szám, tehát megoldást találtunk. Valóban, 7722=595984, megfelel a feltételnek.
A második esetben x=61, és y=8 adódik, ezekből x+y2 háromjegyű szám, innen nem adódik megoldás.
Hasonló gondolatmenettel 21x1, 481x2 alakú tényezőket keresve (9) miatt csak x2=1 vagy 2 lehetséges. Mindkettővel megoldás adódik: x2=1 esetén x1=23, x=23, n=482, y=1, és n2=232324; valamint x2=2 esetén x1=46, x=92, n=964, y=2, és n2=929296. (Az utóbbiban x2, x1, n és y kétszer, n2 és x négyszer akkora, mint az előbbi megoldás megfelelő száma.)
Ha a tényezőket 37x1 és 273x2 alakban keressük, (9) miatt csak x2=2 és 3 jön szóba. x2=2 esetén x1 csak páros lehet, ámde 546-18=528 és 546+18=564 közé 37-nek csak páratlan többszöröse esik: 555=15⋅37. Nem ad megoldást x2=3 sem, mert így x1 páratlan, viszont 3⋅273-18=801 és 3⋅273+18=837 közé 37-nek csak páros többszöröse esik: 814=22⋅37.
Nem adódik megoldás sem 39x1, 259x2 alakú tényezőkkel, sem 91x1, 111x2 alakú tényezőkkel, mert véve x2-nek a (9) megengedte értékeit és a (10) alapján adódó korlátokat, ezek közé x1 együtthatójának vagy nem esik többszöröse, vagy az adódó többszörös párossága nem egyezik x2 párosságával.
Mindezek szerint a feladat feltételeinek a következő három négyzetszám felel meg:
4822=232324,7722=595984és 9642=929296.

2. feladat. Négy egymás utáni páratlan szám összegéhez hozzáadva a számok szorzatát, továbbá a számokból a tényezők ismétlése nélkül képezhető összes kéttényezős és háromtényezős szorzatokat, eredményül 26 879-et kapunk. Melyik ez a négy szám?
 

Megoldás. Tetszés szerinti négy számból, a, b, c, d-ből a feladatban szereplő összeget képezve és egyet hozzáadva szorzattá alakítható kifejezést kapunk, ugyanis
1+(a+b+c+d)+(ab+ac+ad+bc+bd+cd)++(abc+abd+acd+bcd)+abcd=(1+a)(1+b)(1+c)(1+d),


amint az könnyen látható.
Ha a számok egymás utáni páratlan számok, akkor az 1-gyel megnövelt számok egymás utáni páros számok. A köztük középen levő páratlan számot (páratlan számaink közül növekedő sorrendben a harmadikat) x-szel jelölve páros számaink x-3, x-1, x+1, x+3. Ezek szorzatáról tudjuk, hogy 1-gyel nagyobb az adott összegnél, azaz
(x-3)(x-1)(x+1)(x+3)=(x2-9)(x2-1)==x4-10x2+9=26880.(11)


Ebből
x4-10x2-26871=0,x2=5±164.

Csak a pozitív gyökhöz, 169-hez tartozik valós x érték, éspedig x1=13, x2=-13. Ezek páratlan egész számok, így van a feladat feltételeinek megfelelő számnégyes, kettő is: 9, 11, 13, 15 és -17, -15, -13, -11.
 

Megjegyzések. 1. Nem használtuk fel a megoldásban a számok páratlan egész voltát, így elég lett volna csak annyit előírni, hogy 2 különbségű számtani sorozatot alkossanak.
Tovább haladhatunk (11)-ből ezeknek a feltételeknek a kihasználásával és a számtani és mértani közép egyenlőtlenségét használva. (11) pozitív megoldásait keresve a bal oldal a négy egymás utáni páros szám mértani közepének a negyedik hatványa. A számok számtani közepe az x páratlan szám, erre
x>268804>163>12.
x=13-mal próbálkozva 10⋅12⋅14⋅16=26880, s így megoldást kaptunk, 9, 11, 13, 15 kielégíti a feladat követelményeit. Minden tényezőt a negatívjával helyettesítve látjuk, hogy -12-1=-13 is megoldást ad, s így a -17, -15, -13, -11 számok is megfelelnek a feladat követelményeinek. Mivel (11) bal oldalának az értéke x=±1, ±3-ra 0, 3-nál nagyobb abszolút értékű x-ekre pedig x abszolút értékének növekedésével minden tényező abszolút értéke, tehát a szorzat is növekszik, így több megoldás nincs.
 

3. feladat. Az ABC hegyesszögű egyenlő szárú háromszög alapja BC. Határozzuk meg a háromszög köré írható A csúcsú téglalapok közül a legnagyobb és a legkisebb területűt.
 

I. megoldás. Legyen egy az ABC háromszög köré írható, A csúcsú téglalapok közül ADEF úgy, hogy a DE oldal B-n, EF pedig C-n halad át (5. ábra). Így BEC derékszög, ezért E a BC átmérő fölötti Thalész körön van, éspedig ennek azon a félkörén, amelyet a BC egyenes elválaszt A-tól. Jelöljük a kör középpontját (BC felezőpontját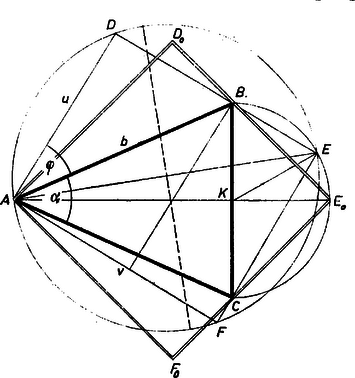) K-val.
 
 
5. ábra
 

a) Megmutatjuk, hogy a keresett legnagyobb területű körülírt téglalapot akkor kapjuk, ha E a mondott félkörív E0 felezőpontjában adódik. Ekkor a körülírt AD0E0F0=N0 téglalap négyzet, mert az AE0 egyenes merőleges BC-re, így felezi a BE0C∢=D0E0F0 szöget.
Ha ADEF=T egy N0-tól különböző, az ABC háromszög köré írt téglalap, akkor átlója rövidebb, mint AE0, mert
AE<AK+KE=AK+KE0=AE0.
Így minden AE átlójú téglalap területe is kisebb, mint N0-é, ugyanis e téglalapok másik két csúcsa az AE átmérőjű körön van, ennek pedig AE-től legtávolabbi pontjai az AE-re merőleges átmérő végpontjai, vagyis az egyenlő átlójú téglalapok közül a négyzet területe a legnagyobb; de még az AE átlójú négyzet területe is kisebb, mint N0-é.
 

b) Az ABC háromszög keresett legkisebb területű körülírt téglalapját akkor kapjuk, ha a téglalap egyik oldala AB vagy AC (e két téglalap szimmetrikus az ABC háromszög tengelyére, így területeik egyenlők). Ekkor ugyanis a téglalap területe 2-szer akkora, mint az ABC háromszögé, és könnyű belátni, hogy körülírt téglalap területe ennél nem lehet kisebb. Ugyanis a B-n át EF-fel párhuzamosan húzott egyenes a körülírt téglalapot és az ABC háromszöget két részre vágja. Mindegyik rész‐téglalapba be van írva egy rész‐háromszög, amelyiknek egyik oldala a téglalap egy oldalán fekszik, és nem nagyobb ennél a téglalapoldalnál, az ehhez tartozó magasság a téglalap szomszédos oldala. Így a két rész‐téglalap területe nem kisebb a rész‐háromszögek területe 2-szeresénél, ugyanez áll tehát az ABC háromszögre és a köré írt téglalapra is. Épp kétszer akkora is csak akkor lehet a körülírt téglalap területe, mint a háromszögé, ha a téglalap egyik oldala egybeesik a háromszög egyik szárával.
 

II. megoldás. Használjuk ismét az I. megoldás jelöléseit, legyen továbbá AC=AB=b, BAC∢=α, AD=u,AF=v, és BAD∢=φ. Az utóbbi szög legkisebb értéke 0, ha ti. T egyik oldala AB; legnagyobb értéke 90∘-α, ha ti. T egyik oldala AC:
0∘≦φ≦90∘-α.(12)
T területe, az ABD és ACF derékszögű háromszögek felhasználásával
t=uv=bcosφ⋅bsin(α+φ),
ugyanis ACF∢=CAD∢=α+φ.
A két szögfüggvény szorzatát a sinzcosw=[sin(z+w)+sin(z-w)]/2 azonosság alkalmazásával összeggé alakítjuk:
t=b22[sin(α+2φ)+sinα].(13)
A zárójelben csak az első tag változik, és (12)-t 2-vel szorozva, valamint mindenütt α-t hozzáadva a változó szögre
α≦α+2φ=180∘-α.(14)
A talált intervallum bal végpontja a feltevés szerint hegyesszög, jobb végpontja tompaszög, közrezárják 90∘-ot. Itt veszi fel (13) első tagja a legnagyobb értékét, 1-et, tehát φ-nek a maximális t-t adó értékére
α+2φ=90∘-bólα2+φ=45∘,
vagyis tmax akkor adódik, ha AD az ABC háromszög AE0 tengelyével 45∘-os szöget zár be. Ekkor a rá merőleges AF oldalegyenes is 45∘-ot zár be AE0-lal, a körülírt téglalap tükrös AE0-ra, tehát négyzet.
Az y=sinx függvény a (14) intervallum (α, 90∘) részintervallumában nő, (90∘, 180∘-a) részintervallumában fogy, így (13) legkisebb értéke az a és 180∘-α végpontokban felvett értékek kisebbike. A két végpontban y=sinx értéke egyenlő, tehát t-nek az
α+2φ=α,azazφ=0∘és azα+2φ=180∘-α,azazφ=90∘-α


értékek esetén egyaránt minimuma van. Az első esetben AD azonos AB-vel (és D azonos B-vel), a másodikban AF azonos AC-vel (és F azonos C-vel).
Ezzel a legnagyobb és legkisebb területű körülírt téglalapok meghatározását befejeztük.
 Lőrincz Pál, Surányi János