Cím: Az 1964. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, kezdők versenye
Szerző(k):  Fried Ervin 
Füzet: 1965/január, 1 - 6. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A) Az általános verseny feladatai

 

1. feladat. Bizonyítsuk be, hogy ha a, b, c pozitív számok, akkor
a3+b3+c3≥a2b+b2c+c2a.(1)
Mikor áll fenn egyenlőség?
 

I. megoldás. Megmutatjuk, hogy az egyenlőtlenség bal oldalából levonva a jobb oldalt, a keletkező k különbség nem lehet negatív. Ha a helyébe b-t, b helyébe c-t, c helyébe a-t, vagy a helyébe c-t, c helyébe b-t, b helyébe a-t írunk, a különbségben csak a tagok sorrendje változik meg, ezért feltehetjük, hogy a a számhármasban előforduló legkisebb érték, azaz
x=b-a≥0ésy=c-a≥0.

Fejezzük ki k-t a, x és y segítségével:
 

k=a3+b3+c3-a2b-b2c-c2a=a3+(a+x)3+k+(a+y)3-a2(a+x)-(a+x)2(a+y)-(a+y)2a=k=2a(x2-xy+y2)+(x3-x2y+y3).
 


Itt egyik zárójeles kifejezés sem negatív, amint az a következő átalakításokból nyilvánvaló:
 


ha x≥y, akkor
x2-xy+y2=x(x-y)+y2≥0,ésx3-x2y+y3=x2(x-y)+y3≥0;
ha pedig x<y, akkor
x2-xy+y2=x2+y(y-x)>0,ésx3-x2y+y3=x3+y(y2-x2)>0.
Egyik esetben sem lehet tehát k negatív.
A fenti átalakításokból látható, hogy 0 is egyedül akkor lesz k, tehát az eredeti egyenlőtlenség két oldala csak akkor egyenlő, ha mind a két zárójeles kifejezés 0. Ez akkor áll fenn, ha x=y és közös értékük 0, azaz ha a=b=c.
 

II. megoldás. Az előző megoldás bevezető meggondolása szerint feltehetjük, hogy a c szám sem a-nál, sem b-nél nem kisebb. A bal és jobb oldal k különbségét így alakítjuk át:
k=a2(a-b)+b2(b-c)+c2(c-a)==a2(a-b)-b2[(c-a)+(a-b)]+c2(c-a)==(a2-b2)(a-b)+(c2-b2)(c-a)=(a+b)(a-b)2+(c+b)(c-b)(c-a).
Itt egyik tag sem negatív, mert sem az elsőben a különbség négyzete, sem a másodikban a különbségek nem negatívok, tehát k≥0.
 

k=0 akkor és csak akkor teljesül, ha mindkét tag 0, tehát ha egyrészt a-b=0, vagyis a=b, amivel a második tag 2. és 3. tényezője egyenlővé válik, másrészt e két tényező közös értéke is 0, tehát akkor és csak akkor, ha a=b=c.
 

Megjegyzések. 1. A feladat állítása könnyen következik Szűcs Adolf következő tételéből1: legyen x1≥x2≥...≥xn≥0, y1≥y2≥...≥yn≥0, legyen továbbá z1, z2, ..., zn az y1, y2, ..., yn számok elrendezése tetszés szerinti sorrendben, akkor
x1y1+x2y2+...+xnyn≥x1z1+x2z2+...+xnzn≥≥x1yn+x2yn-1+...+xn-1y2+xny1.


Ebből feladatunk állítása így következik: Legyen n=3, továbbá tegyük fel továbbra is, hogy a≤b, a≤c. Ha b≤c, legyen x1=c2, x2=b2, x3=a2, y1=c, y2=b, y3=a, z1=a, z2=c, z3=b. Ha pedig b>c, akkor legyen x1=b2, x2=c2, x3=a2, y1=b, y2=c, y3=a, z1=c, z2=a, z3=b. A fenti első egyenlőtlenség mindkét esetben a feladat állítását adja.
 

2. Az egyenlőtlenség helyessége belátható a számok nagyságviszonyára tett minden megszorítás nélkül is, pl. a következő azonosság alapján:
a3+b3+c3-a2b-b2c-c2a==13[(a-b)2(2a+b)+(b-c)2(2b+c)+(c-a)2(2c+a)].



2. feladat. Szerkesszünk háromszöget, ha adott egy oldala, a hozzá tartozó magasság és a rajta levő két szög különbsége.
 

Megoldás. Ha az adott szögkülönbség 0, akkor egyenlő szárú háromszöget kell szerkeszteni az alapjából és az ehhez tartozó magasságból. Ennek megoldása jól ismert, így tovább azzal az esettel foglalkozunk, amikor az adott δ szögkülönbség pozitív.
Legyen ABC a keresett háromszög, a jelölést úgy választva, hogy AB=c legyen az adott hosszúságú oldal, C-nek AB-től való távolsága az adott mc magasság, az A és B csúcsoknál levő α és β szög különbsége pedig δ. Húzzuk meg C-n át az AB-vel párhuzamos d egyenest. Ennek C-ből induló és AB-vel egyező irányú d1 félegyenese CB-vel β nagyságú szöget zár be, az AC oldal C-n túli meghosszabbításával, e-vel bezárt szöge pedig a. Így CB-t d-re tükrözve létrejön az adott szögkülönbség. Jelöljük B tükörképét d-re B'-vel, ekkor CB' is β nagyságú szöget zár be d1-gyel, s így 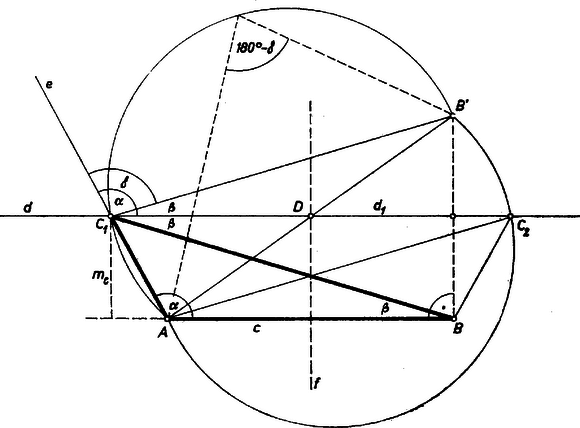CB' és e szöge δ, tehát ACB'∢=180∘-δ.
 

 

1. ábra
 

A d egyenes és B-nek erre vonatkozó tükörképe C ismerete nélkül is megszerkeszthető. Így a következő szerkesztéshez jutottunk: Rajzoljunk c hosszúságú AB szakaszt és az AB egyenes egyik oldalán, tőle mc távolságban egy vele párhuzamos d egyenest. Szerkesszük meg a B pont d-re vonatkozó tükörképét, B'-t. Szerkesszük meg végül azt a körívpárt, amiről az AB' szakasz 180∘-δ szögben látszik. A d egyenes és a körívpár C1 és C2 metszéspontja lehet a háromszög harmadik csúcsa. Ezek meg is felelnek, mert bármelyiket jelölve C-vel, az ABC háromszögben AB=c, az erre merőleges magasság mc, továbbá d-nek a C-ből induló, AB-vel egyirányú félegyenese AC meghosszabbításával α nagyságú szöget zár be. CB'-vel pedig ugyanakkorát, mint a tükörképével, CB-vel, az utóbbi szög szárai pedig ellenkező irányban párhuzamosak β száraival. Így α és β különbsége egyenlő az AC meghosszabbítása és CB' közti szöggel, ami viszont az ACB'∢ kiegészítő szöge, tehát δ.
 

A keletkezett két háromszög egymás tükörképe az AB oldal f felező merőlegesére, ugyanis a körívpár centrál‐szimmetrikus az AB' szakasz D felezőpontjára. Ezen megy át a d egyenes is, mert átmegy BB' felezőpontján és párhuzamos AB-vel. Ugyancsak átmegy D-n f is, mint az ABB' derékszögű háromszög középvonala. Így C1 és C2 az f-re D-ben merőleges d egyenesen D-től egyenlő távolságra van, tehát a két pont egymás tükörképe f-re vonatkozóan.
 

Mivel A és B' a d egyenes különböző partján van, így az egyenes a körívpár mindkét ívét metszi és mindegyiket csak egy pontban, a feladatnak tehát mindig van megoldása és csak egy (ha, mint szokás, egybevágó megoldásokat nem tekintünk lényegesen különbözőknek).
 

3. feladat. Határozzuk meg az ABCD¯ négyjegyű számot úgy, hogy a következő osztás helyes legyen: ABCD¯:D=DBA¯. (A különböző betűk különböző számjegyeket jelölnek.)
 

Megoldás. Írjuk a feltételt szorzat alakban:
DBA¯⋅D=ABCD¯.(2)
Tekintsük először az A és D számjegyeket; első jegy gyanánt csak ezek lépnek fel, így egyikük sem 0.
A szorzat utolsó jegye, ami nem más, mint a D⋅A rész‐szorzat utolsó jegye, egyenlő D-vel, így különbségük, DA-D=D(A-1), osztható 10-zel. Ezért D és A-1 közül legalább az egyik osztható 5-tel, mert 5 törzsszám. Ha D osztható 5-tel, akkor csak D=5 lehet, ha pedig A-1 osztható 5-tel, akkor értéke 5 vagy 0; így az alábbi lehetőségek jönnek szóba:
a)D=5,b)A=6,c)A=1.

Másrészt a szorzandóra:
100D<DBA¯<100(D+1),
és így a szorzatra:
100D2<DBA¯⋅D=ABCD¯<100D(D+1).(3)
Hasonlóan a szorzatra a kezdő jegye alapján:
1000A<ABCD¯<1000(A+1).(4)
A közös belső tag miatt (4) bal oldala kisebb (3) jobb oldalánál, és (3) bal oldala kisebb (4) jobb oldalánál:
1000A<100D(D+1),azaz(5)10A<D2+D,100D2<1000(A+1),azaz(6)D2<10(A+1).

Ezek alapján az a) lehetőség esetében A<3, ill. A>1,5, tehát A=2, így viszont D(A-1)=5, nem osztható 10-zel, ez a feltevés nem vezet megoldásra.
A b) esetben (6) alapján D2<70, D≤8, ezt felhasználva (5)-ből
D2>10A-D=60-D≥52,D>7,
tehát csak D=8 jön szóba. Ekkor azonban a követelményből
(800+10B+6)⋅8=6000+100B+10C+8,2B+C=B+B+C=44,


ami lehetetlen, mert három számjegy összege legfeljebb 27. Innen sem kapunk megoldást.
A hátra levő A=1 esetben (6)-ból D2<20, D≤4, így (5)-ből
D2>10A-D≥10-4=6,D≥3,
D szóba jövő értékei 3 és 4. Ekkor (2)-ből
100D2+10BD+D=1000+100B+10C+D,C+(10-D)B=10(D2-10),


a bal oldal sohasem negatív, a jobb oldal viszont csak D>3 esetén nem az.

A fennmaradt D=4 lehetőség esetében
C+6B=60,
itt C<10 miatt 6B>50, B>8, és a B=9, C=6 jegyekkel megoldást kapunk:
491⋅4=1964,
tehát a keresett szám 1964.
 

A megoldásban nem kellett kihasználnunk, hogy különböző betűk helyére különböző számjegyek írandók, csak azt, hogy kezdő számjegy nem lehet 0.
 

B) A speciális matematikai osztályok versenyének feladatai
Az 1. feladat ugyanaz volt, mint az általános versenyen.
 

2. feladat. Szerkesszünk háromszöget, ha adott valamelyik oldalához tartozó súlyvonala és magasságvonala, továbbá az ugyanezen oldalon fekvő szögek különbsége.
 

Megoldás. Legyen a keresett háromszög ABC, benne a C csúcsnak az AB oldaltól, illetőleg annak F felezőpontjától mért távolsága az adott mc magasság, illetőleg sc súlyvonal, továbbá a CAB és CBA szögek különbsége egyenlő az adott δ szöggel.
Először a δ>0 esettel foglalkozunk. Tükrözzük az ABC háromszöget az AB oldal f felező merőlegesére, C tükörképét jelöljük C'-vel. Ekkor CC' párhuzamos AB-vel, tőle mc távolságra van, C'F=CF=sc, a CC' szakasz látószöge pedig A és B csúcsból a tükrözés folytán a háromszög AB oldalán fekvő szögeinek a különbsége: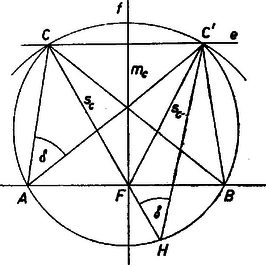
CAC'∢=CBC'∢=δ.
Ezek szerint meg tudjuk szerkeszteni először is a CFC' egyenlő szárú háromszöget mc magasságából és sc szárából: egy e egyenesre egy pontjában f merőlegest állítunk, erre e-től egyik irányban rámérjük mc-t, végpontja F. Az F körüli sc sugarú körrel kimetsszük e-ből a C és C' pontot. Ezután az A és B pontot az F-en át e-vel párhuzamosan húzott egyenesből az az i körív metszi ki, amelyről CC' δ szögben látszik, és amelyik e-nek azon a partján van, amelyiken F.
 

 

2. ábra
 

Az ABC háromszög megfelel a feladat követelményeinek, mert AB-re merőleges magassága mc, miután AB∥CC', CF súlyvonala sc hosszúságú, végül A és B egymás tükörképe f-re, mert az i ív középpontja rajta van a CC' húr felező merőlegesén, f-en, így az A és B csúcsnál levő szögeinek különbsége egyenlő a CAB és C'AB szögek különbségével, ez pedig szerkesztés szerint δ.
 

A másik keletkező háromszög, ABC', az előbbi tükörképe f-re, így nem tekintjük attól különböző megoldásnak.
Nyilvánvaló, hogy a CC'F háromszög akkor és csak akkor jön létre, ha sc>mc. A és B akkor és csak akkor jön létre, ha F benne van abban a körben, melynek része i, vagyis ha CF-nek F-en túli meghosszabbítása metszi ezt a kört. A metszéspontot H-val jelölve ez akkor és csak akkor következik be, ha
CFC'∢>CHC'∢=δ.

Ha δ=0, akkor a háromszög egyenlő szárú, és mc=sc. Így ha e két feltétel egyike teljesül, akkor csak abban az esetben van a követelményeknek megfelelő háromszög, ha a másik is teljesül. Ha ez nem áll, az adatok ellentmondók; ha viszont teljesül, akkor minden mc magasságú, egyenlő szárú háromszög megfelel, így a feladat határozatlan.
 

Összefoglalva: a feladat megoldható, ha sc>mc, továbbá az mc magassággal és sc szárral szerkesztett egyenlő szárú háromszögnek a szárak közti szöge nagyobb δ-nál. E feltételek teljesülése esetén a feladatnak egy megoldása van.
 

3. feladat. Melyik az a legkisebb természetes szám, amelynek első jegyét elhagyva a kapott szám egy prímszám négyszerese, a kapott számra következő szám pedig egy prímszám ötszöröse?
 

Megoldás. A kérdéses szám első jegye nyilván 1, hiszen minden más esetben az első jegy helyére 1-et írva egy ugyanolyan tulajdonságú, de kisebb számot kapnánk.
 

Legyen az első jegy elhagyásával keletkező szám N. A feltétel szerint N=4p és N+1=5q, ahol p és q prímszámok.
Ebből
q=5q-4q=4p+1-4q=4(p-q)+1=4k+1,
és
4p=5q-1=20k+4,azazp=5k+1,
ahol k egész szám. k növekedésével p, és így N is növekszik, ezért feladatunk a legkisebb olyan k egész szám meghatározása, melyre p=5k+1 is, q=4k+1 is prímszám.
Mivel N nem negatív, így p és q sem, és mivel prímek, így 1-nél nagyobbak, tehát k≥1. k páros, mert különben 5 k+1 páros összetett szám lenne. k-nak oszthatónak kell lennie 3-mal is, mert ha 1 maradékot adna, akkor 5k+1 lenne 3-mal osztható és 3-nál nagyobb, tehát összetett, ha pedig 2 maradékot adna, akkor 4k+1. Így 2-vel és 3-mal, tehát 6-tal is osztható szám: k=6n, p=30n+1, és q=24n+1, és feladatunk megkeresni azt a legkisebb n pozitív egész számot, amelyre p is, q is prím.
Kipróbálva n első néhány értékét, az alábbi táblázatban kiírtuk egy‐egy összetettnek adódó érték prímtényezős felbontását:
n=1esetén24n+1=52n=2esetén24n+1=72n=3esetén30n+1=7⋅13,n=4esetén30n+1=112,n=5esetén24n+1=112,n=6esetén24n+1=5⋅29,n=7esetén24n+1=132,n=8esetén30n+1=241,24n+1=193.
Könnyen ellenőrizhető, hogy 241 és 193 mindegyike prím. Így N=4⋅241=964, és a keresett szám 1964.
1V. ö.: Hajós Gy.‐Neukomm Gy.‐Surányi J.: Matematikai versenytételek II. 2. kiadás, Tankönyvkiadó, Budapest, 1965. 44. o.