Cím: 1964. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1965/március, 98 - 107. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Két egybevágó háromoldalú szabályos gúlát alapjuk mentén összeillesztünk. A keletkező hatlapú test minden lapszöge ugyanakkora. Határozzuk meg a két háromélű csúcs távolságának és két négyélű csúcs távolságának az arányát.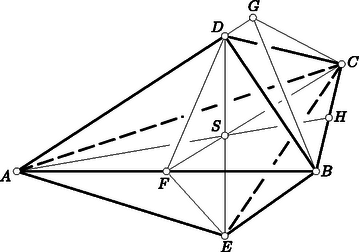

 
I. megoldás. Ha a szabályos ABC▵ mentén összeillesztjük az egybevágó ABCD, ABCE gúlákat (1. ábra), a D, E csúcsok a háromszög síkjára a háromszög S középpontjában emelt merőlegesen helyezkednek el. Az összeillesztéssel keletkező test eszerint nemcsak az ABC síkra, hanem pl. az ADE síkra is szimmetrikus. E szimmetriákból következik, hogy a D, E csúcsokból az AB élre, valamint a B, C csúcsokból az AD egyenesre bocsátott merőlegesek egyenlők, s hogy közös F és G talppontjuk van. Eszerint a DFE∢ az AB él mentén, a BGC∢ pedig az AD él mentén csatlakozó lapok szögét méri. Minthogy e szögek a feltevés szerint egyenlők, a DFE, BGC háromszögek hasonlók, hiszen egyenlő szárúak és szárszögük ugyanakkora.
 
 

1. ábra
 

A hasonlóságból a megfelelő oldalak arányára
DE:BC=DF:BG
következik. A jobb oldali szakaszok az ABD▵ magasságai, s ezért fordítva aránylanak, mint a megfelelő oldalak:
DF:BG=AD:AB.
Minthogy BC=AB, az aránypárok egybevetéséből DE=AD következik, tehát az is, hogy az ADE▵ szabályos, és így hasonló az ABC▵-höz. Ebből a hasonlóságból az oldalak és magasságok arányára
DE:BC=AS:AH
adódik. Minthogy az S súlypont harmadolja az AH súlyvonalat, az utolsó arány értéke 2/3. Ez tehát egyben a DE:BC arány keresett értéke is.
 
Megjegyzés. Feladatunk abból a feltételezésből indul ki, hogy van olyan test, amelyre a feladat követelménye teljesül, azaz lapszögei mind egyenlők. Rámutatunk itt arra, hogy ez valóban igaz, mégpedig éppen úgy jutunk hozzá, hogy a DE:BC arány értékét a megoldásban talált 2/3-nak választjuk, azaz a szabályos ABC▵ középpontjában a háromszög síkjára emelt merőlegesen mindkét irányban a háromszög oldalának harmadát mérjük fel, s az így kapott D, E csúcsok által meghatározott testet tekintjük. Ennek az állításnak a helyessége megoldásunk gondolatmenetének megfordítása útján látható be.
A szerkesztés következménye ugyanis, hogy a megoldásbeli utolsó aránypár teljesül, s ebből következik, hogy az ADE▵ és ABC▵ hasonló, hogy tehát az ADE▵ is szabályos. Eszerint AD=DE, és a középső aránypár jobb oldalán álló arány értéke 2/3. Ennyi tehát a bal oldali arány értéke is, s ezért az első aránypár is helyes. Ebből viszont az egyenlő szárú DFE▵ és BGC▵ hasonlósága adódik, s ezek megfelelő szögeinek egyenlősége miatt a szerkesztett test lapszögei valóban egyenlők.
A szóban forgó testhez a legegyszerűbben talán úgy juthatunk el, hogy egy szabályos ADE▵-et DE oldala körül mindkét irányban 120∘-kal elforgatunk, s az így adódó három háromszög által kifeszített testet tekintjük. Ez közvetlenül adódik a fentiekből.
 
II. megoldás. Az 1. ábra jelöléseit használjuk, és abból indulunk ki, hogy az összeillesztéssel keletkező test az ABC síkra és az ADE síkra is szimmetrikus. Eszerint ez a két sík az AB élű és az AD élű lapszöget felezi, s e lapszögek feltételezett egyenlősége miatt a két sík mindegyike ugyanakkora lapszöget alkot az ABD síkkal.
Tükrözzünk a BAD∢ szögfelezőjében a szög síkjára merőlegesen emelt síkra. E tükrözéskor az AB és AD szárak is, s az imént említett lapszögek egyenlősége miatt az ABC és ADE síkok is helyet cserélnek. Ezért AS metszésvonaluk helyben marad, és a szimmetrikus BAS∢ és DAS∢ egyenlő. Ha tehát a DE szakaszt az AS tengely körül 90∘-kal elforgatjuk, D és ugyanúgy E az AB és AC élre jut, s ezért DE egyenlő az ABC▵-et átvágó, AS-re merőleges B1SC1 szakasszal (2. ábra). Minthogy pedig S az ABC▵ súlypontja, s ez A-tól 2/3-szor akkora távolságra van, mint a BC oldal felezőpontja, a keresett arány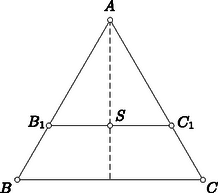
DE:BC=B1C1:BC=23.

 
 

2. ábra
 

III. megoldás. Tekintsük az összeillesztéssel keletkező bipiramis A csúcsú, négyélű szögletét. Ezt a szögletet négy egyenlő szögtartomány határolja, amelyek a feltevés szerint egyenlő lapszögeket alkotva csatlakoznak egymáshoz. Eszerint ez négyoldalú szabályos szöglet, azaz olyan, mint a négyoldalú szabályos gúla csúcsánál elhelyezkedő, amely a gúla tengelye körül 90∘-kal elforgatva önmagát fedi.
Ha tehát a bipiramis DSE tengelyét az A csúcsú szöglet AS tengelye körül 90∘-kal elforgatjuk, akkor az előző megoldásban említett B1C1 szakaszhoz jutunk. Ebből a feladat kérdésére adandó válasz már ugyanúgy következik.
 
Megjegyzés. Utolsó megoldásunk nemcsak azért rövid, mert az előzőre hivatkozott, hanem azért is, mert a szögletekre vonatkozó ismeretekre támaszkodott. Mielőtt ezeket részleteznők, néhány elnevezést említünk meg.
Tekintsünk egy poliédert, annak egyik csúcsát és mindazokat az ebből a csúcsból kiinduló félegyeneseket, amelyeknek egy kezdőszakasza a poliéderhez tartozik. E félegyenesek pontjai együttesen egy végtelenbe nyúló alakzatot alkotnak, amelyet a poliéder szögletének nevezünk. A szöglet legtöbbször végtelenbe nyúló gúla. A szögletet határoló szögtartományok a szöglet oldalai, s a csatlakozó oldalak által alkotott lapszögek a szöglet szögei.
Egy szöglet akkor szabályos, ha minden oldala és minden szöge ugyanakkora. Bebizonyítjuk, hogy a szabályos n-oldalú szögletnek van tengelye, amely körül 360∘/n szöggel elforgatva a szöglet újból ugyanabba a helyzetbe jut. Megoldásunk ezt használta fel az n=4 esetb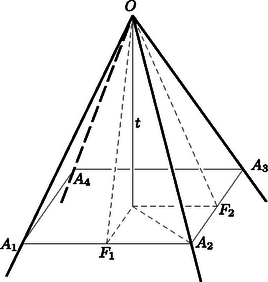en.
 
 

3. ábra
 

Tekintsük az OA1, OA2, ..., OAn élű, n-oldalú szabályos szögletet, (3. ábra). Az A1OA2∢ síkjára az OF1 szögfelező mentén merőleges síkot emelünk. Ezt a síkot az OA2 élű lapszöget felező sík a t egyenesben metszi. A szabályosság miatt A1OA2∢=A2OA3∢, s ezért e szögek a lapszögüket felező A2Ot síkra vonatkozólag szimmetrikusan helyezkednek el. Ebből a szimmetriából következik, hogy az F1Ot sík tükörképe az A2OA3∢ síkját annak OF2 szögfelezőjében metszi, s hogy OF1 és OF2 ugyanakkora szöget zár be a t egyenessel. Ha tehát a szögletet t körül az F1Ot, F2Ot síkok hajlásszögével elforgatjuk, akkor az A1OA2 oldal fedi az A2OA3 oldalt. Minthogy pedig a szabályos szöglet szögei egyenlők, az elforgatott A2OA3 oldal az A3OA4 síkba kerül, és a szöglet oldalainak egyenlősége miatt az OA3 él az OA4 helyzetbe jut. Ugyanígy következtethetünk azonban tovább, és megállapíthatjuk, hogy valamennyi oldal és él a rákövetkezőnek a helyét foglalja el. Ha tehát ezt az elforgatást n-szer megismételjük, mindegyik az n-edik rákövetkezőt, azaz önmagát fedi. Eszerint ez az n-szeres elforgatás 360∘-os, és egy elforgatás valóban ennek n-edrésze.
Ha n páros, legyen n=2k. Ekkor a k-szoros elforgatás 180∘-os, tehát a tengelyre vonatkozó tükrözést jelent. Ebben az esetben kimondhatjuk tehát, hogy a tengely az átellenes élek szögét felezi. Megoldásunk az n=4 esetben ezt is felhasználta.
 
Második feladat. Egy táncmulatságon minden fiú táncolt legalább egy lánnyal, de egy sem táncolt mindegyikkel, és ugyanígy minden lány táncolt legalább egy fiúval, de nem mindegyikkel. Bizonyítsuk be, hogy kiválasztható a táncmulatság résztvevői közül két fiú és két lány úgy, hogy e két fiú mindegyike a két lány közül csak az egyikkel táncolt, és ugyanígy a két lány mindegyike is csak az egyikkel táncolt a két fiú közül.
 
I. megoldás. A fiúkat osztályozhatjuk aszerint, hogy ki hány lánnyal táncolt. Tartozzék F1 azok közé a fiúk közé, akik a legtöbb lánnyal táncoltak. Minthogy F1 sem táncolt minden lánnyal, van olyan L1 lány, akivel F1 nem táncolt. Van viszont olyan F2 fiú, aki táncolt L1-gyel, hiszen L1 is táncolt legalább egy fiúval.
F1 megválasztása miatt F2 nem táncolhatott több lánnyal, mint ahánnyal F1 táncolt. Ebből következik, hogy F2 nem táncolhatott mindazokkal a lányokkal, akikkel F1 táncolt, mert az ellenkező esetben F2 több lánnyal táncolt volna, mint F1, hiszen F2 táncolt L1-gyel is, F1 pedig nem. Van tehát olyan L2 lány, akivel F1 táncolt, de F2 nem.
Az F1, F2 fiúk és L1, L2 lányok kielégítik a feladat követelményét, hiszen F1 és L1, valamint F2 és L2 nem táncoltak egymással, viszont F1 táncolt L2-vel és F2 táncolt L1-gyel.
 
Megjegyzés. A feladat feltevései közül csak azt használtuk fel, hogy egyik fiú sem táncolt minden lánnyal, s hogy minden lány táncolt legalább egy fiúval. Ugyanígy persze elég lett volna csak arra támaszkodnunk, hogy egyik lány sem táncolt minden fiúval, s hogy minden fiú táncolt legalább egy lánnyal, hiszen a fiúk és a lányok szerepét a megoldásban is felcserélhetjük. Két lehetőséget találtunk tehát a feladat szövegének módosítására, feltevéseinek gyengítésére.
Bár közvetlenebb és egyszerűbb megoldást nem tudunk adni, mégis ismertetünk további megoldásokat, mert ezek révén további érdekes kapcsolatokra és általánosításokra mutathatunk rá. Az előző bekezdés észrevétele a további megoldásokra is vonatkozik.
 
II. megoldás. Válasszunk ki a résztvevők közül egy F1 fiút és egy L1 lányt, akivel F1 nem táncolt. Legyen továbbá F2 olyan fiú, aki táncolt L1-gyel, és L2 olyan lány, akivel F2 nem táncolt. Ezt a kiválasztást ugyanígy folytatjuk: Fi kiválasztása után (i=2,3,...) olyan Li lányt választunk, akivel Fi nem táncolt, majd olyan Fi+1 fiút, aki táncolt Li-vel. Addig folytatjuk ezt, amíg nem kerülne sor olyannak a kiválasztására, akit korábban már kiválasztottunk. Minthogy a táncmulatságon véges sokan vesznek részt, ez előbb-utóbb bekövetkezik. Eszerint ki lehet választani k fiút és k lányt, és ezeket körbe lehet úgy állítani, hogy minden fiút két lány fogjon közre, és minden fiú táncolt a balján álló lánnyal, de nem táncolt a jobbján állóval. Azt kell bebizonyítanunk, hogy ez már két fiúval és két lánnyal is megvalósítható.
Legyenek egy ilyen körben állók sorjában
F1,L1,F2,L2,...,Fk,Lk,
ahol tehát azt is tudjuk, hogy F1 és Lk táncoltak egymással. Megmutatjuk, hogy ha k>2, akkor kevesebb fiúból és lányból is tudunk ilyen kört alkotni. Ha ugyanis F1 táncolt L2-vel, akkor
F1,L1,F2,L2,
ha pedig F1 nem táncolt L2-vel, akkor
F1,L2,...,Fk,Lk
elégíti ki a követelményt. Eszerint a létszám mindig tovább csökkenthető, amíg csak két fiúhoz és két lányhoz el nem jutunk.
 
Megjegyzés. Ha a résztvevőket pontokkal ábrázoljuk, és az egymással táncolókat ábrázoló pontokat egy-egy vonallal kötjük össze, egy gráf szögpontjaihoz és éleihez jutunk. Ha a vonalak esetleg metszik egymást, metszéspontjukat nem mondjuk a gráf szögpontjának.
A kapott gráfot páros gráfnak mondjuk, mert szögpontjai két osztályba sorolhatók (ti. a fiúkat és a lányokat ábrázoló szögpontokéba) olyan módon, hogy minden él két más-más osztályba tartozó szögpontot köt össze. Kiegészíthetjük ezt a gráfot azáltal, hogy éllel kötünk össze minden más-más osztályba tartozó két szögpontot. Ennek az élei tehát kétfélék: vagy szerepeltek már az eredeti gráfban is, vagy csak utóbb csatoltuk hozzá. Ezt a kétféleséget azzal szemléltethetjük, hogy az éleket két színnel színezzük meg.
Mondhatjuk tehát, hogy feladatunk egy két színnel megfestett teljes páros gráfról szól. Bármelyik szögpontot tekintjük is, a belőle kiinduló élek a feladat feltevése szerint nem mindannyian ugyanolyan színűek. A feladat már bebizonyított állítása szerint található az ilyen gráfban négy csatlakozó él által alkotott ,,négyszög'', amelynek az élei váltakozva más-más színűek.
Ez az átfogalmazás már a bizonyítás során is alkalmazható lett volna. Az olvasóra hagyjuk, hogy ezt a valamivel szemléletesebb megfogalmazást végiggondolja. Felhívjuk azonban a figyelmet arra, hogy a két szín között nincs semmiféle szerepkülönbség. Ez annak felel meg, hogy eredeti feladatunk tartalma mit sem változik, ha benne az ,,egymással táncolt'' és ,,egymással nem táncolt'' fogalmakat felcseréljük. Ha másodszor is összegyűlnek a résztvevők, de most csak azok táncolnak egymással, akik az első alkalommal nem táncoltak, akkor is ugyanazok elégítik ki a feladat állításának követelményeit.
Megoldásunk gondolatmenete változatlanul alkalmazható akkor is, ha nem teljes páros gráfról, hanem teljes gráfról beszélünk, azaz olyanról, amelyben minden szögpontpárt él köt össze. Ennek az ellenőrzését is az olvasóra hagyjuk. Megelégszünk azzal, hogy az így bizonyított állítást a következő szemléletes alakban adjuk elő: Egy társaságban egyesek ismerik egymást, mások nem; senki sem ismer mindenkit, de mindenkinek van ismerőse a társaságban; kiválasztható akkor a társaság négy tagja, s ezek leültethetők egy kerek asztal köré úgy, hogy két szomszédja közül mindenki csak az egyiket ismerje. Ehhez az eredményhez az első megoldás módszerével is könnyen eljuthattunk volna.
 
III. megoldás. Feltesszük, hogy a táncmulatság résztvevői közül nem választhatók ki négyen a követelményt kielégítő módon, s ebből a feltevésből ellentmondásra következtetünk, ti. arra, hogy akkor a táncmulatságnak végtelen sok résztvevője van. Ezáltal a feladat állításának helyességét bizonyítjuk be.
Legyen L1 az egyik lány és F1 olyan fiú, aki táncolt L1-gyel. Legyen L2 olyan lány, aki nem táncolt F1-gyel, és F2 olyan fiú, aki táncolt L2-vel. Megállapíthatjuk, hogy F2 táncolt L1-gyel, mert különben (L1, F1, L2, F2) kielégítené a feladat követelményét. Az eddig említett résztvevők közül eszerint csak L2 és F1 nem táncoltak egymással.
Tegyük fel, hogy már találtunk olyan
L1,F1,L2,F2,...,Lk,Fk
résztvevőket, akik közül ketten csak akkor nem táncoltak, ha a lány indexe a fiúénál nagyobb. Ez volt a helyzet k=2 esetében. Megmutatjuk most, hogy a sorozat kiegészíthető Lk+1, Fk+1 résztvevőkkel olyan módon, hogy a kiegészített sorozat is rendelkezzék az eredeti sorozat tulajdonságával. Ebből majd valóban következik, hogy a kiegészítés minden határon túl folytatható, hogy tehát végtelen sok résztvevő van.
Minthogy Fk táncolt az L1,...,Lk lányok mindegyikével, van olyan további Lk+1 lány, akivel nem táncolt. Ez az Lk+1 lány nem táncolt az F1,...,Fk-1 fiúkkal sem, pl. Fi-vel azért, mert különben (Lk, Fk, Lk+1, Fi) kielégítené a követelést. Minthogy Lk+1 nem táncolt az F1,...,Fk fiúk egyikével sem, van olyan további Fk+1 fiú, akivel táncolt. Ez az Fk+1 fiú táncolt az L1,...,Lk lányokkal is, pl. Li-vel azért, mert az ellenkező esetben (Li, Fi, Lk+1, Fk+1) kielégítené feladatunk követelését. Ezek szerint a kiegészített
L1,F1,L2,F2,...,Lk,Fk,Lk+1,Fk+1
sorozat valóban rendelkezik azzal a tulajdonsággal, hogy egy sorozatbeli lány és fiú csak akkor nem táncolt egymással, ha kettejük indexe közül a lányé a nagyobb.
 
Megjegyzés. Megoldásunk arra is rámutatott, hogy a feladat állítása végtelen sok résztvevő, pontosabban végtelen sok fiú és végtelen sok lány részvétele esetén már nem helyes. Egy ellenpéldát, talán még mindig szemléletesen, a következőképpen adhatunk elő: Egy végtelen nagy társaságban senkinek a magassága sem éri el a 180cm-t, de bármily kevéssel kisebb magasságot adunk is meg, már található olyan fiú is és olyan lány is, aki azt a magasságot eléri; minden fiú csak a nála kisebb lányokkal táncol. Könnyű ellenőrizni, hogy ekkor a feladat feltevései teljesülnek, viszont nem választható ki két fiú és két lány a feladat követelményét kielégítő módon.
Ez az ellenpélda természetesen megszövegezhető úgy is, hogy csak gráfokról szólunk. Felvetjük most a megfelelő kérdést végtelen teljes gráfokra is. Kérdezzük tehát, hogy ha egy végtelen sok szögpontú teljes gráf éleit úgy színezzük meg két színnel, hogy egy szögpontból se induljon ki csupa ugyanolyan színű él, vajon mindig igaz-e, hogy a gráf tartalmaz váltakozó színű négyszöget. Olyan példát adunk meg, amely mutatja, hogy ez sem igaz. Tartozzék a természetes számok mindegyikéhez egy-egy szögpont; az a, b számokhoz tartozó szögpontokat összekötő él legyen piros vagy kék aszerint, hogy a és b nagyobbika páros-e vagy páratlan. Könnyű ellenőrizni, hogy itt a feltételek teljesülnek, viszont váltakozó színű négyszög nem található.
 
IV. megoldás. Tudjuk, hogy minden fiúhoz található olyan lány, akivel nem táncolt. Lehetséges, hogy bármely két fiúhoz is található olyan, akivel egyikük sem táncolt. Talán bármely három vagy esetleg még több fiúhoz is található mindig ilyen lány. Van mindenesetre egy legnagyobb k érték, amelyre még igaz, hogy bármely k fiúhoz található olyan lány, akivel egyikük sem táncolt. Ez a k kisebb, mint a táncmulatságon résztvevő fiúk száma, hiszen minden lány táncolt legalább egy fiúval.
Minthogy k+1 már nem rendelkezik k tulajdonságával, kiválasztható k+1 fiú:
F1,F2,...,Fk+1
olyan módon, hogy minden lány táncolt valamelyikükkel. Ha közülük egyet, pl. F1-et elhagyjuk, a megmaradó k fiúhoz k tulajdonsága miatt található olyan L1 lány, akivel egyikük sem táncolt, s ezért vele a k+1 fiú közül csak F1 táncolt. Ugyanígy okoskodhatunk, ha a k+1 fiú közül nem F1-et, hanem egy másikat hagyunk el. Ilyen módon olyan
L1,L2,...,Lk+1
lányokhoz jutunk, akiknek mindegyike csak az ugyanolyan indexű fiúval táncolt a k+1 fiú közül.
Minthogy k≥1, az F1, F2 fiúkról és az L1, L2 lányokról minden esetben szó lehet, s ezek kielégítik a feladat követelményét.
 
Megjegyzés. Valamivel rövidebb volna ez a megoldás, ha befejezésekor csak L1 és L2 létezésére következtetnénk, hiszen csak erre volt szükség. Így viszont a következő, a feladat állításánál többet mondó eredményhez is eljutottunk: Ha egy táncmulatságon minden lány táncol legalább egy fiúval, és bármely k fiúhoz található olyan lány, akivel egyikük sem táncolt, akkor kiválasztható a résztvevők közül k fiú és k lány úgy, hogy ezek mindegyike táncolt ezek valamelyikével, mégpedig mindenki csak eggyel.
Megoldásunk gondolatmenete ismét alkalmazható akkor is, ha nem egy teljes páros gráf, hanem egy teljes gráf két színnel való megszínezéséről van szó. Az olvasó könnyen ellenőrizheti, hogy így a következőképpen megfogalmazható eredményhez jutunk: Egy társaságban mindenkinek van ismerőse, de a társaság bármely k tagjához található olyan, akit egyikük sem ismer; ekkor kiválasztható a társaságnak 2k tagja, s ezek leültethetők egy asztal két oldalán olyan módon, hogy a szemközti oldalon ülők közül mindenki csak a vele szemben ülőt ismerje.
 
Harmadik feladat. Bizonyítsuk be, hogy tetszőleges a, b, c, d pozitív számokra
a2+b2+c2+d24≥abc+abd+acd+bcd43.

I. megoldás. Be kell bizonyítanunk, hogy a köbgyök alatti kifejezés nem nagyobb a bal oldal köbénél. Felhasználjuk a számtani és a mértani középre vonatkozó ismert egyenlőtlenséget, amely szerint két szám szorzata nem lehet a számtani közepük négyzeténél nagyobb. Ezt kétszer is alkalmazva
abc+abd+acd+bcd4=12[abc+d2+cda+b2]≤≤12[(a+b2)2c+d2+(c+d2)2a+b2]=a+b2⋅c+d2⋅a+b+c+d4≤≤(a+b+c+d4)2a+b+c+d4=(a+b+c+d4)3.
Elég most már csak azt igazolnunk, hogy
a+b+c+d4≤a2+b2+c2+d24.
Ez abból adódik, hogy a kétoldali kifejezések négyzetének különbsége
a2+b2+c2+d24-(a+b+c+d4)2==116[3(a2+b2+c2+d2)-2(ab+ac+ad+bc+bd+cd)]==116[(a-b)2+(a-c)2+(a-d)2+(b-c)2+(b-d)2+(c-d)2]≥0.



Megjegyzés. A feladat szövegében felesleges az a megszorítás, hogy a, b, c, d pozitív számok. Ezt megoldásunk sem használta fel. Igaz ugyan, hogy hivatkoztunk a számtani és mértani közép egyenlőtlenségére, és mértani középről csak pozitív értékek körében beszélhetünk, viszont pozitív értékekre való szorítkozás nélkül is igaz, hogy két szám szorzata nem lehet a számtani közepük négyzeténél nagyobb.
Megoldásunk az eredetinél erősebb
a+b+c+d4≥abc+abd+acd+bcd43
egyenlőtlenséget bizonyította be. A következő megoldások is ezt igazolják majd.
Megoldásainkban többféle középérték szerepel. A pozitív a1, a2,...,an számok számtani (aritmetikai), mértani (geometriai), harmonikus és négyzetes (kvadratikus) közepét az
A(a1,...,an)=1n(a1+...+an),G(a1,...,an)=a1...ann,H(a1,...,an)=n1a1+...+1an,Q(a1,...,an)=a12+...+an2n
képletek adják meg. Ezek között sokféle egyenlőtlenség állapítható meg. Két számra vonatkozólag már felhasználtuk a G≤A egyenlőtlenséget. Négy számra vonatkozólag bebizonyítottuk, hogy A≤Q. Két számra vonatkozólag közvetlenül ellenőrizhető a
G2=AH
összefüggés, és ebből G≤A felhasználásával H≤G, és így H≤A is adódik. Bizonyítás nélkül említjük meg, mert nem lesz szükségünk rá, hogy az itt említett egyenlőtlenségek n szám közepeire is teljesülnek.
 
II. megoldás. Jelölje A, G, H, Q az a, b, c, d számok megfelelő közepeit. Feladatunk állítása köbreemelés után Q3≥G4/H alakban írható, s mi a többet mondó G4≤A3H egyenlőtlenséget bizonyítjuk be.
Jelölje A1, G1, H1 az a, b számok, A2, G2, H2 pedig a c, d számok megfelelő közepeit. Nyomban belátható, hogy ezekre
A(A1,A2)=A,G(G1,G2)=G,H(H1,H2)=H.
Mivel G12=A1H1, és hasonló érvényes bármely két szám közepeire,
G4=G12G22=A1H1⋅A2H2=A1A2⋅H1H2==A(A1,A2)⋅H(A1,A2)⋅A(H1,H2)⋅H(H1,H2).
Minthogy pedig H(A1,A2)≤A(A1,A2), és a hasonló H1≤A1, H2≤A2 egyenlőtlenségekből A(H1,H2)≤A(A1,A2) következik, a fenti egyenlőségből a bizonyítandó G4≤A3H egyenlőtlenséghez jutunk.
 
III. megoldás. Felhasználjuk azt, hogy ha négy szám nem egyenlő, akkor van közöttük a számtani közepüknél nagyobb, és van kisebb is. Legyen például c<A<d, ahol A ismét az a, b, c, d számok számtani közepét jelöli. Legyen c1=c+d-A és d1=A. Ezekre
c1+d1=c+d,c1d1=(c+d-A)A=(A-c)(d-A)+cd>cd.
Ha tehát az a, b, c, d számok helyébe az a, b, c1, d1 számokat írjuk, számtani közepük változatlanul A marad, viszont A is szerepel közöttük, illetőleg többször szerepel, mint ahányszor szerepelt, és a feladat egyenlőtlenségének jobb oldala
ab(c+d)+(a+b)cd<ab(c1+d1)+(a+b)c1d1
miatt növekszik.
Ha tehát a, b, c, d nem egyenlők, akkor megváltoztathatók úgy, hogy számtani közepük változatlanul A maradjon, A többször szerepeljen közöttük, mint ahányszor szerepelt, s hogy a feladatbeli köbgyök értéke növekedjék. Ezt az eljárást a szükség szerint megismételve mindegyik szám helyébe A lép, s a köbgyök értéke állandóan növekszik. Ha pedig mindegyik szám A-val egyenlő, akkor a köbgyök értéke is A. Eszerint a köbgyök értéke eredetileg is A-nál kisebb vagy esetleg vele egyenlő volt, s ez az, amit bizonyítani akartunk.
 
Megjegyzés. Ennek a megoldásnak a gondolatmenete változatlanul alkalmazható akkor is, ha nem négy számról és a belőlük képezhető három tényezős szorzatok összegéről, hanem n számról és az ezekből képezhető k tényezős szorzatok összegéről van szó. Így azt kapjuk, hogy ez az összeg nem lehet nagyobb, mint (nk)Ak.
Kiemeljük ennek az eredménynek azt a speciális esetét, amikor k=n-1. Ebben az esetben a vizsgált összeg nGn/H. Így tehát a
Gn≤An-1H
egyenlőtlenséghez jutunk, amely n=2 esetén egyenlőség formájában teljesül, n=4 esetén pedig a megoldásainkban bizonyított egyenlőtlenséggel azonos.
Gondolatmenetünk még a k=n esetben is alkalmazható, amikor csak egyetlen szorzatról van szó, s így az n szám közepeire érvényes G≤A egyenlőtlenség bizonyításához jutunk.