Az 1964. évi Országos Középiskolai Matematikai Verseny II. fordulóján kitűzött feladatok között szerepelt a következő: Ha $\alpha$, $\beta$, $\gamma$ egy háromszög szögei, akkor $\text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma <2$. Több versenyző megmutatta, hogy a bal oldal $3/2$-nél sem lehet nagyobb, és ekkora is csak a szabályos háromszög esetében lesz. ¹
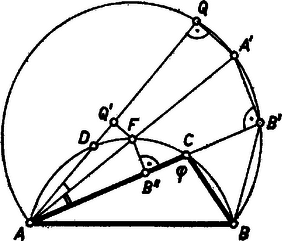Kézenfekvő a szögek szinuszainak az összegére is felső korlátot keresni. Az alábbiakban mindkét összeget alkalmas távolságösszeggel fogjuk szemléltetni és megmutatjuk, hogy mindkét összeg a szabályos háromszög esetén a legnagyobb, azaz

 

1. ábra

AC(CB) húr $C$ végpontja. Ez utóbbi azért igaz, mert ha $FD<FC$, akkor $DAF\sphericalangle <FAC\sphericalangle$, és így ‐ $F$ merőleges vetületét $AQ$-n $Q\text{'}$-vel, $AB\text{'}$-n $B\text{'}\text{'}$-vel jelölve ‐ $FQ\text{'}<FB\text{'}\text{'}$, mert az $AQ\text{'}F$ és $AB\text{'}\text{'}F$ derékszögű háromszögek átfogói egyenlők. Ezért igaz az is, hogy ha $0<\widehat{QA\text{'}}<\widehat{B\text{'}A\text{'}}$ ‐ a rövidebb ívekről van szó a mondott végpontok között ‐, akkor $AB\text{'}<AQ<AA\text{'}$.
Most már választ adhatunk első kérdésünkre. Megmutatjuk, hogy (2) bal oldala a szabályos háromszög esetén a legnagyobb, azaz egy körbe írható háromszögek közül a szabályos háromszög kerülete a legnagyobb.
Legyen az $ABC$ háromszögnek ${60}^{\circ }$-tól különböző szöge. Ekkor szögei közt biztosan van olyan, amelyik nagyobb, és olyan, amelyik kisebb, mint ${60}^{\circ }$. Válasszuk a betűzést úgy, hogy a háromszög legnagyobb szöge a $B$ csúcsnál, a legkisebb szöge az $A$ csúcsnál legyen (4. ábra). Így $C$-nél hegyesszög van. Tükrözzük az $ABC$ háromszöget az $AB$ oldal felező merőlegesére. Az $ABC\text{'}$ tükörkép egybevágó $ABC$-vel, tehát kerületük egyenlő.
Tekintsük azt az $A$ kezdőpontú félegyenest, mely az $AB$ félegyenessel ${60}^{\circ }$-os szöget zár be, és $AB$-nek ugyanazon oldalán van, mint $C$. Messe ez a félegyenes a háromszög köré írt kört $D$-ben. Mivel $BAC\sphericalangle <{60}^{\circ }$, és $BAC\text{'}\sphericalangle >{60}^{\circ }$, azért az $AD$ félegyenes a $CAC\text{'}$ szögtartomány belsejében halad. Ugyanez a szögtartomány tartalmazza a kör $ACB$ ívének $F$ felezőpontját is. Eszerint $D$ közelebb van $F$-hez, mint akár $C$, akár $C\text{'}$, így segédtételünk szerint az $ABD$ háromszög kerülete nagyobb az $ABC$ háromszög kerületénél.
Ha most a kör $BAD$ ívének $G$ felezőpontját tekintjük, akkor ‐ hasonlóan ‐ a $BGD$ háromszög kerülete nagyobb a $BAD$ háromszög kerületénél vagy egyenlő vele, a $BGD$ háromszög pedig szabályos. (Egyenlő akkor, ha $G$ egybeesik $A$-val, $ACB\sphericalangle ={60}^{\circ }$.)
Ezzel igazoltuk, hogy a körbe írt szabályos háromszög kerülete bármely más, ugyanezen körbe írt háromszög kerületénél nagyobb; így (2) bal oldala akkor maximális, ha $\a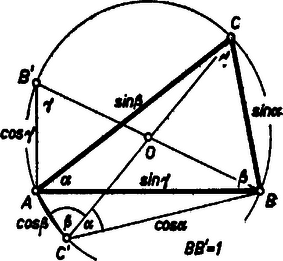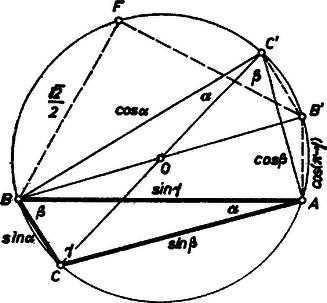lpha =\beta =\gamma ={60}^{\circ }$, azaz

$\begin{array}{c}{\displaystyle \text{sin}\alpha +\text{sin}\beta +\text{sin}\gamma \le 3\sqrt[]{3}/\mathrm{2,}}\end{array}$

és egyenlőség csak $\alpha =\beta =\gamma$-ra teljesül.

 

 

2. ábra

 

 

3. ábra

 

Most adjunk (1) bal oldalának is geometriai jelentést. (A körülírt kör átmérője most is egységnyi legyen.) Tükrözzük a háromszög $B$ és $C$ csúcsát az $O$ középpontra, tükörképeik legyenek $B\text{'}$ és $C\text{'}$ (2. és 3. ábra). A kerületi szögekre vonatkozó tétel miatt
${\displaystyle \begin{array}{c}\hfill {\displaystyle B\text{'}A=\text{cos}\gamma \mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">illetve</span>}\gamma >{90}^{\circ }\text{<span style="font-weight: normal;font-style: normal;">esetén</span>}B\text{'}A=\text{cos}\left(\pi -\gamma \right)\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">és</span>}}\hfill \\ \hfill {\displaystyle C\text{'}A=\text{cos}\beta \mathrm{,}C\text{'}B=\text{cos}\alpha \mathrm{.}}\hfill \end{array}}$

(1) bal oldalát elég hegyesszögű háromszögre vizsgálni. Ha ugyanis az $ABC$ háromszög nem hegyesszögű $\left(\gamma \ge {90}^{\circ }\right)$, a háromszög-egyenlőtlenség miatt (3. ábra)

$\begin{array}{c}{\displaystyle \text{cos}\beta +\text{cos}\gamma =\text{cos}\beta -\text{cos}\left(\pi -\gamma \right)=AC\text{'}-AB\text{'}\le B\text{'}C\text{'}\mathrm{,}}\end{array}$

ahol az egyenlőség csak $\gamma ={90}^{\circ }$-ra teljesül. Ezért segédtételünk miatt

$\begin{array}{c}{\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma \le \text{cos}\alpha +B\text{'}C\text{'}\le BF+FB\text{'}=\sqrt[]{2}<\frac{3}{2}\mathrm{.}}\end{array}$

Mellékesen tehát azt is beláttuk, hogy (1) bal oldala ‐ nem hegyesszögű háromszögekre szorítkozva ‐, maximálisan $\sqrt[]{2}$ lehet, és ezt a határt csak $\alpha =\beta ={45}^{\circ }$ esetén éri el.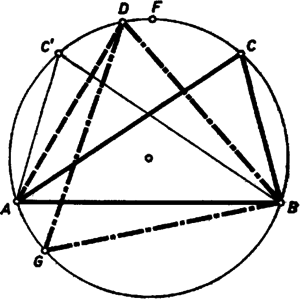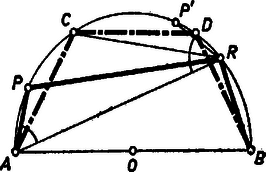

 

 

4. ábra

 

 

5. ábra

 

Ha háromszögünk hegyesszögű, akkor tartalmazza a körülírt kör $O$ középpontját, s ekkor az (1) bal oldala a $BB\text{'}$ egységátmérőjű félkörbe írt három szakaszból (húrból) álló törött vonal hosszával egyenlő (2. ábra). Így arra a kérdésre kell választ adnunk, hogy az $AB$ félkörbe írt $AP+PR+RB$ húrösszeg (5. ábra) mikor a legnagyobb.
A félkör $AP$, $PR$, $RB$ ívei között legyen olyan, melyhez ${30}^{\circ }$-tól különböző kerületi szög tartozik. Ekkor van köztük olyan, amelyikhez ${30}^{\circ }$-nál nagyobb, és olyan is, amelyikhez kisebb kerületi szög tartozik, feltehetjük, hogy az $AP$ ívhez tartozik a legkisebb, és a következő $PR$-hez a legnagyobb kerületi szög. (Különben véve $P$-nek és $R$-nek $O$-ra való tükörképét, $P\text{'}$-t és $R\text{'}$-t, az $APRBP\text{'}R\text{'}$ centrálszimmetrikus hatszög csúcsaiból vett alkalmas egymásra következő $4$ megfelel feltételünknek.) Rajzoljuk meg azt az $R$ kezdőpontú félegyenest, mely $RA$-val ${30}^{\circ }$-os szöget alkot, és $RA$ ugyanazon oldalán van, mint $P$, messe ez az $APR$ ívet $C$-ben. Mivel $ARP\sphericalangle <{30}^{\circ }$ és $PAR\sphericalangle >{30}^{\circ }$, ha az $AR$ felező merőlegesére $P$-t tükrözzük, az $RC$ félegyenes a $PRP\text{'}$ szögtartományban halad, és ugyanez a szögtartomány tartalmazza az $APR$ körív felezőpontját. Az előzőek szerint, mivel $C$ e felezőponthoz közelebb van, mint $P$ vagy $P\text{'}$

$\begin{array}{c}{\displaystyle AC+CR>AP+PR\mathrm{.}}\end{array}$

Ha most tekintjük a $CRB$ körív $D$ felezőpontját, akkor

$\begin{array}{c}{\displaystyle CD+DB\ge CR+RB\mathrm{,}}\end{array}$

és egyenlőség csak akkor áll, ha $RB$ ívhez ${30}^{\circ }$-os kerületi szög tartozik. Így

$\begin{array}{c}{\displaystyle AC+CD+DB>AP+PR+RB}\end{array}$

és

$\begin{array}{c}{\displaystyle AC=CD=DB\mathrm{.}}\end{array}$

Ezzel beláttuk, hogy a félkörbe írt három, sugárnyi hosszú húr összege nagyobb bármely más e félkörbe írt megfelelő húr összegénél, tehát egy $AB$ félkörbe írt $AP+PR+RB$ húrösszeg ‐ ha a pontok sorrendje $A$, $P$, $R$, $B$ ‐ akkor a legnagyobb, ha $AP=PR=RB$. Így (1) bal oldala akkora legnagyobb, ha $\alpha =\beta =\gamma ={60}^{\circ }$, azaz

$\begin{array}{c}{\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma \le 3/\mathrm{2,}}\end{array}$

és egyenlőség csak $\alpha =\beta =\gamma$ esetén áll.
A továbbiakban (1) és (2) egy-egy általánosítását adjuk.
Ha $\alpha$, $\beta$, $\gamma$ egy háromszög szögei, akkor bármely pozitív egész $n$-re

$\begin{array}{c}{\displaystyle \sqrt[{\phantom{1}}^n]{\text{sin}\alpha }+\sqrt[{\phantom{1}}^n]{\text{sin}\beta }+\sqrt[{\phantom{1}}^n]{\text{sin}\gamma }\le 3\sqrt[{\phantom{1}}^n]{\frac{\sqrt[]{3}}{2}}\mathrm{,}}\end{array}$

(3)

továbbá, ha $\alpha$, $\beta$, $\gamma$ egyike sem tompaszög, akkor

$\begin{array}{c}{\displaystyle \sqrt[{\phantom{1}}^n]{\text{cos}\alpha }+\sqrt[{\phantom{1}}^n]{\text{cos}\beta }+\sqrt[{\phantom{1}}^n]{\text{cos}\gamma }+\le 3\sqrt[{\phantom{1}}^n]{\frac{1}{2}}\mathrm{.}}\end{array}$

(4)

A bizonyítást csak az $n=2^k$ esetre végezzük el $k$-ra vonatkozó teljes indukcióval.
A $k=0$-ra (egy szám ,,első gyökén'' magát a számot értve) bizonyítottuk az állítást. Tegyük fel, hogy (3) és (4) fennáll $n=2^k$-ra, ahol $k>0$; bebizonyítjuk, hogy akkor fennáll $n=2^{k+1}$-re is. Tekintsük a következő összegeket:
${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\alpha }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\beta }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\gamma }\mathrm{,}}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle \sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\alpha }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\beta }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\gamma }\mathrm{.}}\hfill & \text{(<mn>6</mn>)}\end{array}}$


Felhasználjuk, hogy nem negatív számok mértani közepe nem nagyobb számtani közepüknél. Ha $u$, $v$, $w\ge 0$, akkor
${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(\sqrt[]{u}+\sqrt[]{v}+\sqrt[]{w}\right)}^2=\left(u+v+w\right)+2\left(\sqrt[]{uv}+\sqrt[]{uw}+\sqrt[]{vw}\right)\le \left(u+v+w\right)+}\hfill \\ \hfill {\displaystyle +2\left(\frac{u+v}{2}+\frac{u+w}{2}+\frac{v+w}{2}\right)=3\left(u+v+w\right)\mathrm{.}}\hfill \end{array}}$

Eszerint (5) és (6) négyzetére

$\begin{array}{c}{\displaystyle {\left(\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\alpha }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\beta }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{sin}\gamma }\right)}^2\le 3\left(\sqrt[{\phantom{1}}^{2^k}]{\text{sin}\alpha }+\sqrt[{\phantom{1}}^{2^k}]{\text{sin}\beta }+\sqrt[{\phantom{1}}^{2^k}]{\text{sin}\gamma }\right)\le 9\sqrt[]{\frac{\sqrt[]{3}}{2}}\mathrm{,}}\end{array}$

illetve

$\begin{array}{c}{\displaystyle {\left(\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\alpha }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\beta }+\sqrt[{\phantom{1}}^{2^{k+1}}]{\text{cos}\gamma }\right)}^2\le 3\left(\sqrt[{\phantom{1}}^{2^k}]{\text{cos}\alpha }+\sqrt[{\phantom{1}}^{2^k}]{\text{cos}\beta }+\sqrt[{\phantom{1}}^{2^k}]{\text{cos}\gamma }\right)\le 9\sqrt[{\phantom{1}}^{2^k}]{\frac{1}{2}}}\end{array}$

igaz az indukciós feltevés miatt, amiből négyzetgyökvonással adódik az állítás.
Pogáts Ferenc

---

¹Surányi János: Az 1964. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulóján kitűzött feladatok megoldása, K. M. L. 29 (1964) 106. o.